1.NumPy基础

2.线性代数

3.微积分

4.概率统计

5.信息论

6.随机过程

7.强化学习

8.概率图模型

9.构建目标函数

学好数学，将使您更具创新能力！

本例是数学在构建多分类任务的损失函数时的一个经典应用

多分类的目标函数可作为二分类的推广，多分类任务的学习过程如下：

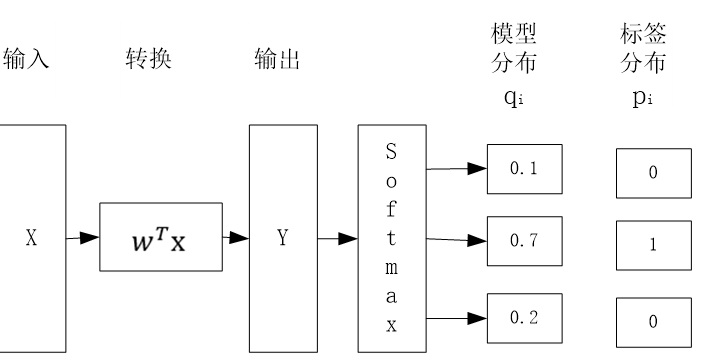
模型分布服从多项分布，其对数似然函数为：
logp(x|w)=\sum_{i}^C p_i logq_i
为计算最大似然估计，把上式添加负号，并对各样本进行累加可得，多分类任务的损失函数为：
L(w)=\frac{-1}{m}\sum_i^m\sum_j^C p_{ij} logq_{ij}
其中m表示样本总数，c表示类别总数
P_{ij}表示样本i的真实类别为1，否则取0。
q_{ij}表示样本i属于类别j的预测值或概率值。
上式实际上就是模型分布与标签分布的交叉熵，这个交叉熵可以很好衡量模型分布与标签分布的差异，同时通过迭代法求该损失函数最小值的过程，等价于进行最大似然估计的过程，实现了最小化损失函数与进行最大似然估计的完美统一！
对其原理有一定了解后，自然对这种损失函数的优缺点会有进一步认识。以交叉熵构成的损失函数一般把标签转换为独热编码(One-Hot）,这样标签向量中只有一个1其余都是0，这说明它只关心对于正确标签预测概率的准确性，忽略了其他非正确标签的差异。如果类别数很多或有些类别是相近的（如同不同角度的同一个人脸），这种方式就有点过于严苛，为此改进这些不足，人们想到了很多优化方法，比如对softmax进行改进，如L-Softmax、SM-Softmax、AM-Softmax等。