1.1大模型Emergent Abilities（新兴能力）现象

模型规模达到某个阈值时，模型对某些问题的处理性能呈现快速增长。这个过程类似于水加热到100度的过程。
目前一些大模型已达或接近这个阈值，个人觉得这些技术或方法功不可没：
一、软件方面
1.BP算法
2.注意力机制
3.强化学习
强化学习一大贡献就是弥补了传统机器学习评估标准的不足，传统机器学习一般基于损失函数进行评估，希望预测与标签的差平方（或两者的分布近似度）越小越好。这种评估方式是一种绝对值的近似，不利于输出多样性的结果。而强化学习采用奖励或评分的方式，看重的是输出与期望值的对齐程度。

4.大数据平台，如PyTorch，TensorFlow，及CUDA架构等
5.GEMM
二、硬件方面
GPU、TPU等地助力。

1.2 几种正助力拓展序列长度的几种算法

（1）FlashAttention，FlashAttention-2
FlashAttention从软件和硬件两个方面对Transformer模型进行优化，软件方面采用了分块、在线softmax，重计算（一种类似于Python迭代器的思路，用规则或算法表示数据，而不实际存在大数据）；硬件方法，充分考虑了GPU的架构特点，如A100,H100等HBM,SRAM等优缺点。

HBM,SRAM等优缺点

（2）Learned、Relative、RoPE等位置编码方法

（3）多种注意力机制

1.3.各种大模型使用技术概览

下面我选择8个比较典型的大模型，统计了它们使用的一些技术，供大家参考。

————————————————
版权声明：本文为CSDN博主「wumg3000」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/wumg3000/article/details/135242873

目录
第1章 AIGC概述
1.1 AIGC主要技术
1.2 生成模型与判别模型
1.3 生成模型的底层逻辑
1.4 表示学习
1.5 表示学习的逆过程
第2章 深度神经网络
2.1 用PyTorch构建深度神经网络
2.2用PyTorch从零开始实现神经网络
2.3用PyTorch-Lightning实现神经网络实例
2.4构建卷积神经网络
2.5 构建循环神经网络
2.6 迁移学习的基本原理
2.7 深度学习常用归一化方法
2.8 权重初始化
2.9 PyTorch常用的损失函数
2.10深度常用优化算法
第3章 变分自编码器
3.1自动编码器
3.2变分自动编码器
3.3构建变分自编码器
3.4实现变分自编码器
第4章 生成对抗网络
4.1 生成对抗网络简介
4.2 从零开始用GAN网络生成图像
4.3 GAN面临的问题
4.4 WGAN
4.5 WGAN-GP
第5章 StyleGAN模型
5.1 StyleGAN的前身ProGAN简介
5.2 StyleGAN架构
5.3 StyleGAN主要算法
5.4 用PyTorch从零开始实现StyleGAN
5.5 StyleGAN的最新进展
5.6 DragGAN简介
第6章 风格迁移
6.1 Deep Dream模型
6.2 风格迁移
6.3 使用PyTorch实现图像修复
6.4 风格迁移与StyleGAN模型
第7章 注意力机制
7.1注意力机制概述
7.2 带注意力机制的编码器-解码器架构
7.3自注意力
7.4如何训练含自注意力的模型？
7.5交叉注意力
第8章 Transformer模型
8.1 直观理解Transformer架构
8.2 用PyTorch从零开始实现Transformer
第9章 大语言模型
9.1大语言模型概述
9.2 可视化GPT原理
9.3 GPT-3简介
9.4可视化BERT原理
9.5 用PyTorch实现BERT
9.6 用GPT-2生成文本
第10章 ChatGPT模型
10.1 ChatGPT概述
10.2 人类反馈的强化学习
10.3 Codex
10.4 如何使LaTeX转换为自然语言？
10.5 使用PPO算法优化CartPole游戏
10.6使用RLHF算法提升GPT-2性能
10.7 ChatGPT如何提升思维链推断能力？
10.8 ChatGPT如何提升模型的数学逻辑推理能力？
第11章 扩散模型
11.1 扩散模型概述
11.2用PyTorch从零开始编写DDPM
第12章 多模态模型
12.1 CLIP简介
12.2 Stable Diffusion模型
12.3 从零开始实现Stable Diffusion
12.4 Stable Diffusion 升级版
12.5 DALL.E概述
附录：AIGC的数学基础
A矩阵基本运算
B 随机变量及其分布
C:信息论
D:推断
D.1极大似然估计
D.2 极大后验概率估计
D.3 EM算法
D.4变分推断
D.5马尔可夫链蒙特卡罗随机采样
E:强化学习
E.1 强化学习基本概念
E.2 强化学习基础算法
E.3策略梯度

第3章 ChatGPT简介

3.1ChatGPT厚积薄发

最近，工智能公司OpenAI推出的ChatGPT风靡全球，其上线仅两个月，注册用户破亿。ChatGPT包含丰富的知识，不仅能更好地理解人类的问题和指令，流畅进行多轮对话，还在越来越多领域显示出解决各种通用问题和推理生成能力。许多人相信，ChatGPT不仅是新一代聊天机器人的突破，也将为信息产业带来巨大变革，也预示着AI技术应用将迎来大规模普及。
ChatGPT表现不俗？其背后的技术有哪些？

3.2 从GPT到GPT-3

3.3 从GPT-3到ChatGPT的进化路线图

下图为从最初的GPT-3到GPT-3.5的进化路线图。
图1 GPT-3初版到ChatGPT的进化路线图
其中text—davinci—002是在code—davinci—002的基础上使用InstructGPT训练方法改进的。GPT-3.5在GPT-3的基础上加入了代码的能力，ChatGPT的代码训练中，很多数据来自于类似Stack Overflow这样一些代码问答的网站，所以我们会发现它做简单的任务其实做得还蛮好的。
从图1可知，GPT-3为ChatGPT打下了扎实的基础，但codex、RLHF等技术新增很多新功能，挖掘了GPT-3的潜力。

3.4 使GPT-3初版升级到ChatGPT的多项关键技术

从图1可知，这两项关键技术是代码训练（Codex）、RLHF及TAMER等
1、Codex
Codex 模型系列是 GPT-3 系列的后代，它经过了自然语言和数十亿行代码的训练。 该模型系列精通十几种语言，包括 C# JavaScript、Go、Perl、PHP、Ruby、Swift、TypeScript、SQL甚至Shell，但最擅长 Python。
你可以使用Codex完成各种任务，包括：
 将注释转换为代码
 在上下文中补全下一行代码或函数
 为你提供一些知识，例如为应用程序查找有用的库或 API 调用
 添加注释
 重写代码以提高效率
Codex如何训练的呢？
首先，在GITHub数据上预训练模型。这个模型可以合理地表征人类编码空间，可以极大地减少搜索量级。使用带tempering的GOLD目标函数，结合编程竞赛数据集，微调模型。可有进一步降低搜索空间，给每个编程题目生成一个较大的样本集；过滤这个样本集，得到一个较小的候选结果集。
然后，进行代码补全，代码补全这个任务的特殊性：具体来说，传统的NLP任务，生成的结果越接正确答案，那么模型得分越高，但是代码不是这样的，代码但凡有一点点小Bug，都可能造成毁灭性的结果。所以对于代码补全任务，判断生成代码的正确与否就是使用的单元测试（unit test）。
针对代码补全这样一个特殊问题，作者提出了一个pass@k的一个指标，生成k个结果，只要有一个通过就算通过（k如果比较大，就会对模型的能力过度乐观，当k比较大的时候，虽然模型分数比较高，但是在使用时，会给用户返回一大堆代码，让用户去选，这个也是很难的，所以说需要排算法，但这个分数并没有反映排序）。

评估Codex模型使用了Github及HumanEval等数据集。
在预训练过程中引入程序代码，和文本一起参与预训练，以此进一步增强大型语言模型（Large Language Model，LLM）的推理能力。这个结论从不少论文的实验部分都可以得出。如图3所示。
图3 有关codex的试验数据
从图3给出的实验数据，来自于论文“On the Advance of Making Language Models Better Reasoners”，其中GPT-3 davinci就是标准的GPT-3模型，基于纯文本训练；code-davinci-002（OpenAI内部称为Codex）是同时在Code和NLP数据上训练的模型。如果比较两者效果，可以看出，不论采用具体哪种推理方法，仅仅是从纯文本预训练模型切换到文本和Code混合预训练模型，在几乎所有测试数据集合上，模型推理能力都得到了巨大的效果提升。
2、RLHF
人类反馈强化学习（Reinforcement Learning from Human Feedback，RHFL）模型将预训练语言模型按照人类反馈进一步微调以符合人类偏好，利用人类反馈信息直接优化模型。Open AI 采用了人类反馈强化学习作为ChatGPT和核心训练方式，并称其是“能有效提升通用人工智能系统与人类意图对齐的技术”。RLHF 的训练包括三个核心步骤：
（1）预训练语言模型（也可以使用额外文本进行微调，监督微调新模型可以让模型更 加遵循指令提示，但不一定符合人类偏好）。
（2）对模型根据提示（prompt）生成的文本进行质量标注，由人工标注者按偏好从最 佳到最差进行排名，利用标注文本训练奖励模型，从而学习到了人类对于模型根据给定提 示生成的文本序列的偏好性。
（3）使用强化学习进行微调，确保模型输出合理连贯的文本片段，并且基于奖励模型 对模型输出的评估分数提升文本的生成质量。
详细过程如图4所示。
图4 RHFL的训练过程，
原图来自：Learning to summarize from human feedback
3、TAMER
TAMER（Training an Agent Manually via Evaluative Reinforcement，评估式强化人工训练代理）框架。该框架将人类标记引入到智能体（即强化学习中的Agents）的学习循环中，可以通过人类向Agents提供奖励反馈（即指导Agents进行训练），从而快速达到训练任务目标。其架构图如下所示。

3.5 ChatGPT训练过程

3.6 ChatGPT不断迭代的路线图

图5 ChatGPT不断迭代的路线图

3.7ChatGPT的不足

尽管ChatGPT在上下文对话能力甚至编程能力上表现出色，完成了大众对人机对话机器人由“人工智障”到“人工智能”的突破，我们也要看到，ChatGPT仍然有一些局限性，还需不断迭代进步。
（1）ChatGPT在其未经大量语料训练的领域缺乏“人类常识”和引申能力，甚至会一本正经的“胡说八道”。
（2）ChatGPT无法处理复杂冗长或者特别专业的语言结构。对于来自金融、自然科学或医学等专业领域的问题，如果没有进行足够的语料“喂食”，ChatGPT可能无法生成适当的回答。
（3）ChatGPT还没法在线的把新知识纳入其中，而出现一些新知识就去重新预训练GPT模型也是不现实的。
（4）训练ChatGPT需要耗费非常大量的算力，成本还是很大的。

3.8 ChatGPT应用场景

ChatGPT能够提供高效的信息获取方式，有望成为重要的生产工具，潜在应用领域广泛。业界普遍认为，ChatGPT将在智能办公、智慧科研、智慧教育、智慧医疗及游戏、新闻等领域迅速落地。在金融、传媒、文娱、电商等领域，ChatGPT可以为各类消费群体提供个性化、高质量的服务，解锁多领域智慧应用。

第2章 GPT-3简介

GPT-3依旧延续自己的单向语言模型训练方式，只不过这次把模型尺寸增大到了1750亿，并且使用45TB数据进行训练。同时，GPT-3主要聚焦于更通用的NLP模型，GPT-3模型在一系列基准测试和特定领域的自然语言处理任务（从语言翻译到生成新闻）中达到最新的SOTA结果。对于所有任务，GPT-3没有进行任何微调，仅通过文本与模型进行交互。与GPT-2相比，GPT-3的图像生成功能更成熟，不需经过微调，就可以在不完整的图像样本基础上补全完整的图像。GPT-3意味着从一代到三代的跨越实现了两个转向：
1.从语言到图像的转向；
2.使用更少的领域数据、甚至不经过微调步骤去解决问题。

2.1 预训练模型一般流程

一般预训练模型（如ELMo、BERT等）的流程如图1-23所示，其中微调是一个重要环节。

图1-23 预训练模型的一般流程

2.2 GPT-3 与BERT的区别

一般预训练模型中微调是一个重要环节，但GPT-3却无需微调，GPT-3与一般预训练模型（这里以BERT为例）还有很多不同之处，具体可参考图1-24。
图1-24 GPT-3 与BERT的区别

2.3 GPT-3与传统微调的区别

对下游任务的设置大致有以下四类：
1.Fine-Tunning（FT）：
FT利用成千上万的下游任务标注数据来更新预训练模型中的权重以获得强大的性能。但是，该方法不仅导致每个新的下游任务都需要大量的标注语料，还导致模型在样本外预测的能力很弱。虽然GPT-3从理论上支持FT，但没有采用这种方法。
2.Few-Shot（FS）
模型在推理阶段可以得到少量的下游任务示例作为限制条件，但是不允许更新预训练模型中的权重。
3.One-Shot（1S）
模型在推理阶段仅得到1个下游任务示例。
4.Zero-Shot（0S）
模型在推理阶段仅得到一段以自然语言描述的下游任务说明。GPT-3与传统预训练模型对下游任务的处理方法的区别，可参考图1-25。

图1-25 传统微调与GPT-3采用的三种设置方法比较

2.4 GPT-3 示例

图1-26 为使用GPT-3 进行文本纠错的实例，从纠错结果来看，效果还是令人惊奇。
图1-26 GPT-3 进行文本纠错的实例

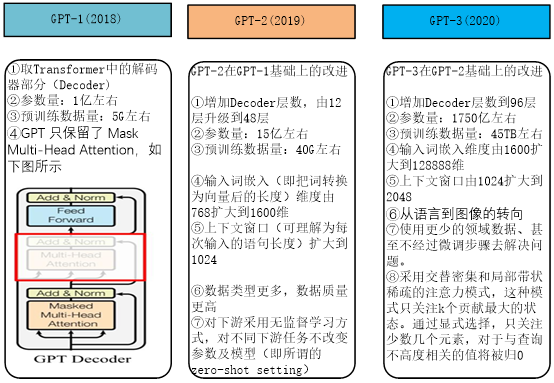
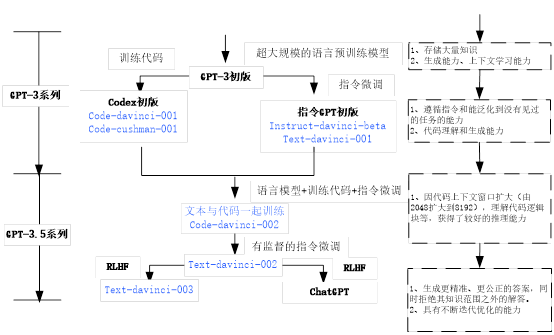
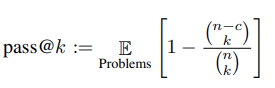
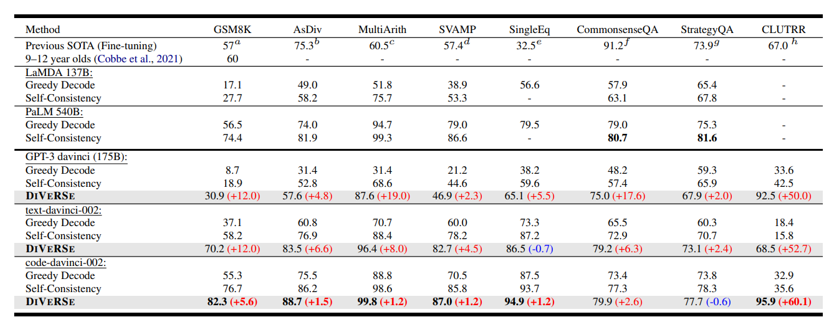
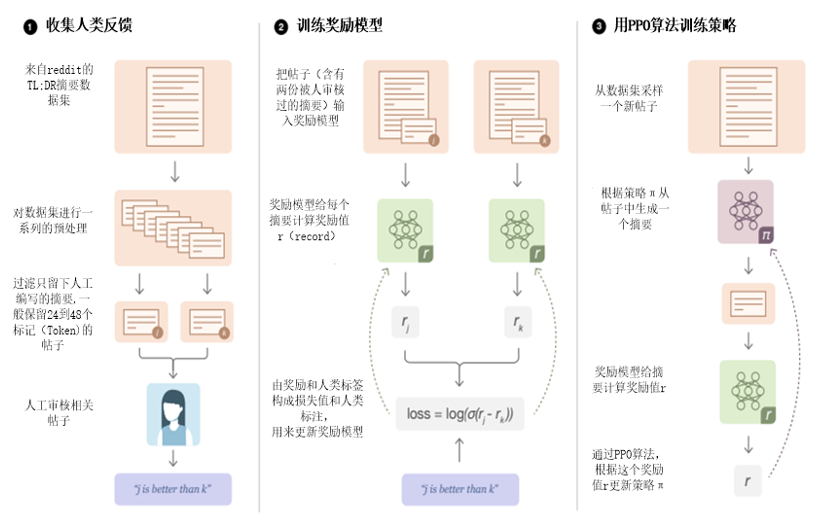
第1章 可视化GPT原理

BERT预训练模型采用了Transformer的Encoder部分，这节介绍的GPT（包括GPT-2、GPT-3）使用Transformer的Decoder部分。

1.1 GPT简介

GPT来自OpenAI的论文《Improving Language Understanding by Generative Pre-Training》，后来又在论文《Language Models are Unsupervised Multitask Learners》提出了 GPT-2 模型。GPT-2 与 GPT 的模型结构差别不大，但是采用了更大、更高质量的数据集进行实验。
GPT 是在 Google BERT算法之前几个月提出的，与 BERT 最大的区别在于，GPT和后来的一些模型，如TransformerXL和XLNet本质上是自回归（auto-regressive）模型，即使用单词的上文预测单词，而 BERT 不是，它采用使用MLM模型，同时利用单词左右来预测。因此，GPT 更擅长处理自然语言生成任务 (NLG)，而 BERT更擅长处理自然语言理解任务 (NLU)。

1.2 GPT的整体架构

GPT 预训练的方式和传统的语言模型一样，通过上文，预测下一个单词,GPT的整体架构如图1-11所示。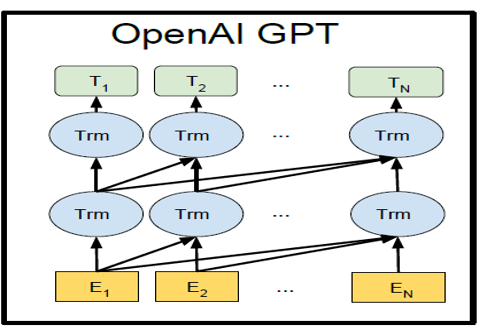

图1-11 GPT的整体架构图
其中Trm表示Decoder模块，在同一水平线上的Trm表示在同一个单元，E_i表示词嵌入，那些复杂的连线表示词与词之间的依赖关系，显然，GPT要预测的词只依赖前文。
GPT-2根据其规模大小的不同，大致有4个版本，如图1-12所示。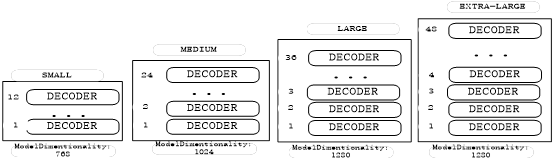

图1-12 GPT-2的4种模型

1.3 GPT模型结构

GPT、GPT-2使用 Transformer的Decoder 结构，但对 Transformer Decoder 进行了一些改动，原本的 Decoder 包含了两个 Multi-Head Attention 结构，GPT 只保留了 Mask Multi-Head Attention，如图1-13所示。

图1-13 GPT的模型结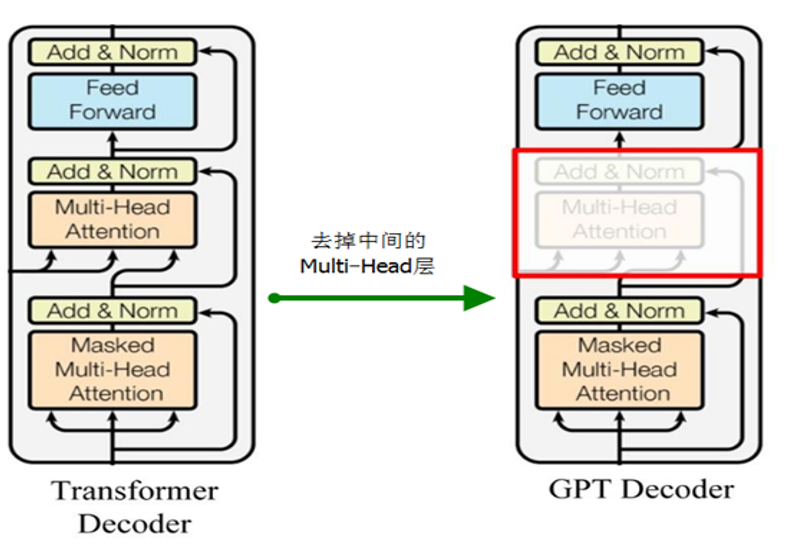构

1.4 GPT-2的Mult-Head与BERT的Mult-Head区别

BERT使用Muti-Head Attention ,可以同时从某词的左右两边进行关注。而GPT-2采用Masked Muti-Head Attention，只能关注词的右边，如图1-14所示。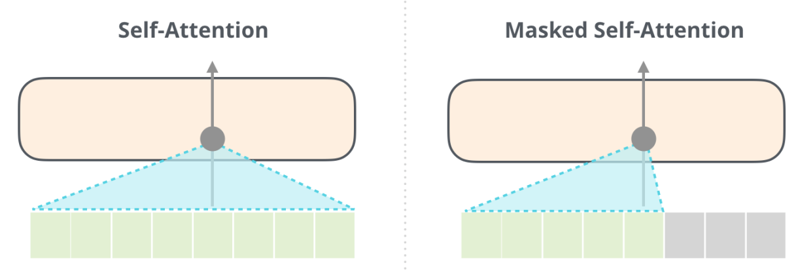

图1-14 BERT与GPT-2的Multi-Head的异同

1.5 GPT-2的输入

GPT-2的输入涉及两个权重矩阵，一个是记录所有单词或标识符（Token）的嵌入矩阵(Token Embeddings)，该矩阵形状为mode_vocabulary_size xEmbedding_size，另一个为表示单词在上下文位置的编码矩阵（Positional Encodings），该矩阵形状为:context_sizexEmbedding_size，其中Embedding_size根据GPT-2模型大小而定，SMALL模型为768，MEDIUM为1024，以此类推。输入GPT-2模型前，需要把标识嵌入加上对应的位置编码，如图1-15所示。

图1-15 GPT-2 的输入数据
在图1-15中，每个标识的位置编码在各层DECODER是不变的，它不是一个学习向量。

1.6 GPT-2 计算Masked Self-Attention的详细过程

假设输入语句为："robot must obey orders"，接下来must这个query对其它单词的关注度（即分数），主要步骤：
（1）对各输入向量，生成矩阵Q、K、V;
（2）计算每个query对其它各词的分数；
（3）对所得的应用Mask（实际上就是乘以一个下三角矩阵）
详细步骤如下：
1.创建矩阵Q、K 、V
对每个输入单词，分别与权重矩阵$W^Q,W^K,W^V$相乘，得到一个查询向量（query vector）、关键字向量（key vector）、数值向量（value vector），如图1-16所示。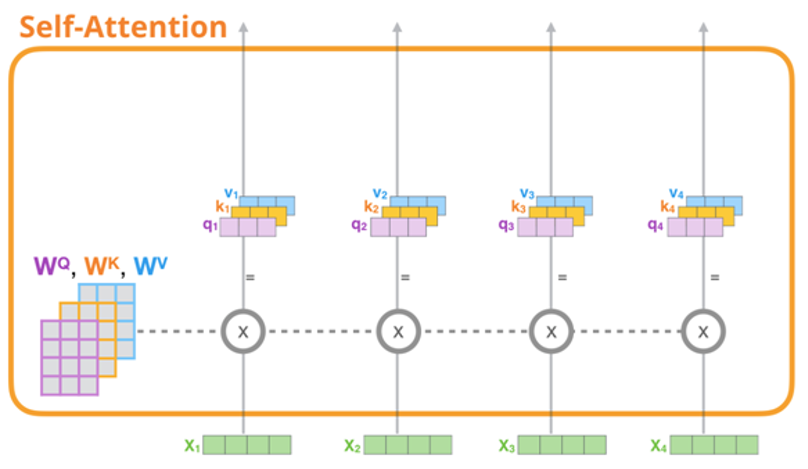

图1-16 生成self-Attention中的K,Q,V
2.计算每个Q对Key的得分
对每个Q对Key的得分计算公式，如图1-17所示。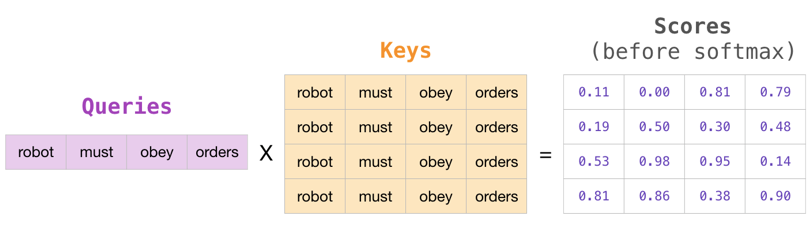

图1-17 Q对key得分的计算过程
3.对所得的分数应用Mask
对所得分再经过Attention Mask的映射，如图1-18所示。

图1-18 得分经过Mask示意图
4.Mask之后的分数通过softmax函数
经过Mask后的分数通过softmax后的结果如图1-19所示。

图1-19 得分通过softmax后
5.单词must（即q2）对各单词的得分为：
q2对各单词的得分，如图1-20所示。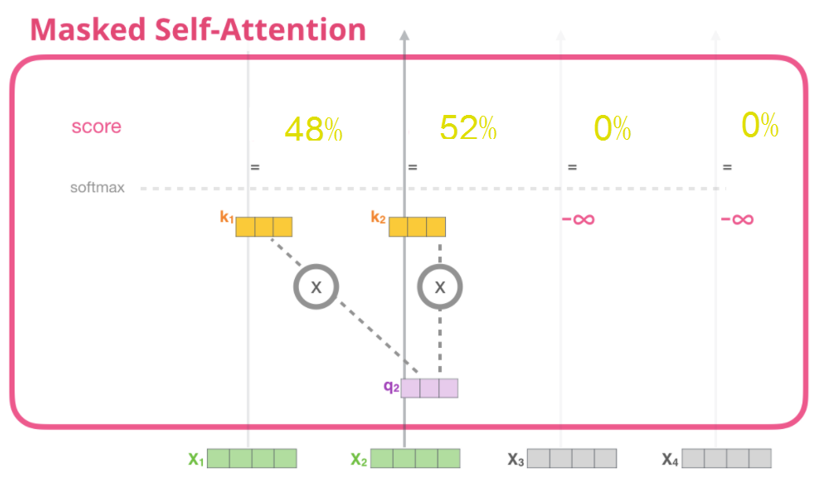

图1-20 q2对各词的得分

1.7 输出

在最后一层，对每个词的输出乘以Token Embedding矩阵（该矩阵的形状为mode_vocabulary_size xEmbedding_size，其中Embedding_size的值根据GPT-2的型号而定，如果是SMALL型，就是768，如果是MEDIUM型，就是1024等），最后经过softmax函数，得到模型字典中所有单词的得分，通过取top取值方法就可得到预测的单词，整个过程如图1-21所示。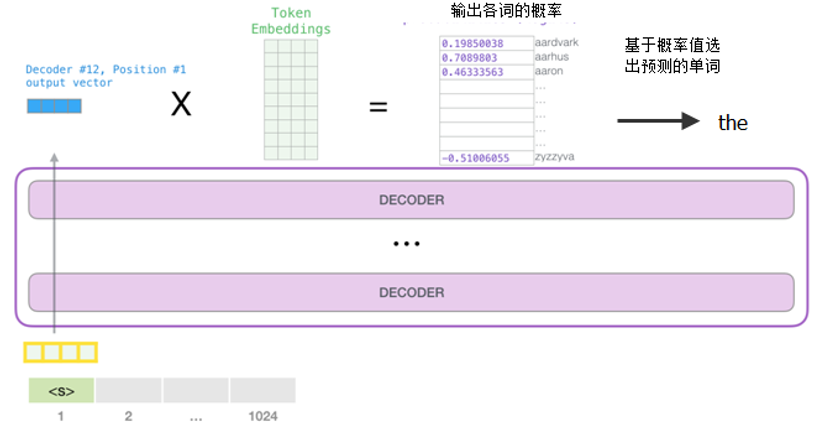

图1-21 GPT-2的输出

1.8 GPT与GPT-2的异同

在GPT的基础上，后面又开发出GPT-2，两者架构上没有大的变化，只是对规模、数据量等有些不同，它们之间的异同如下：
1.结构基本相同，都采用LM模型，使用Transformer的DECODER。
2.不同点：
（1）GPT-2结构的规模更大，层数更大。
（2）GPT-2数据量更大、数据类型更多，这些有利于增强模型的通用性，并对数据做了更多质量过滤和控制。
（3）GPT对不同的下游任务，修改输入格式，并添加一个全连接层，采用有监督学习方式，如图1-22所示。而GPT-2对下游采用无监督学习方式，对不同下游任务不改变参数及模型（即所谓的zero-shot setting）。

图1-22（左）Transforer的架构和训练目标，（右）对不同任务进行微调时对输入的改造。
GPT如何改造下游任务？微调时，针对不同的下游任务，主要改动GPT的输入格式，先将不同任务通过数据组合，代入Transformer模型，然后在模型输出的数据后加全连接层（Linear）以适配标注数据的格式，具体情况大致如下：
1.分类问题，改动很少，只要加上一个起始和终结符号即可；
2.句子关系判断问题，比如Entailment，两个句子中间再加个分隔符即可；
3.文本相似性判断问题，把两个句子顺序颠倒下做出两个输入即可，这是为了告诉模型句子顺序不重要；
4.多项选择问题，则多路输入，每一路把文章和答案选项拼接作为一个输入即可。
从图1-22可看出，这种改造还是很方便的，不同任务只需要在输入部分改造即可，所以GPT-2、GPT-3 对不同下游任务基本不改过参数和模型方式。

5.3.5 EM算法的收敛性
要证明通过迭代法求得的参数$\{\theta _{t}\}$收敛于极值点，如果能证明对应的似然函数$\mathcal L(\theta_t)$收敛即可。要证明似然函数收敛，因似然函数$\mathcal L(\theta)$有上界，如果能证明通过迭代，似然函数递增，则$\mathcal L(\theta_t)$收敛于极值点。
假设第t次迭代时的参数为$\theta_{t}$，通过t+1次迭代后参数为$\theta_{t+1}$，接下来证明$\mathcal L(\theta_{t+1})\geq \mathcal L(\theta_{t})$。
由式（5.13）可得：
运算结果与隐变量$z_i$无关，是一个常数，根据Jensen不等式可知，式（5.12）中作为第t次迭代的结果，即把$\theta$视为$\theta_{t}$，$Q_i(z_i)$改为$Q_{it}(z_i)$，则其中不等式可以取等号，即有：
似然函数与其下界函数之间的关系，可以通过图5-10直观表示。
图5-10 EM算法中目标函数与下界函数的之间的关系

5.3.4 EM算法推导

通过构建目标函数的下界函数来处理隐含变量的似然函数，该下界函数更容易优化，并通过求解下界函数的极值，构造新的下界函数，通过迭代的方法，使下界函数收敛于局部最优值。
假设概率分布$p(x|\theta)$生成可观察样本为$X=\{x_1,x_2,\cdots,x_n\}$,这n个样本互相独立，以及无法观察的隐含数据为$Z=\{z_1,z_2,\cdots,z_n\},\{X,Y\}$构成完整数据，样本的模型参数为$\theta$。完整数$\{x_i,z_i\}$的似然函数为：$p(x_i,z_i|\theta)$
下界函数通过隐变量的概率分布构造，对每个样本$x_i$，假设$Q_i$为隐变量$z_i$的一个概率密度函数，它们满足概率的规范性，即有：
$\sum_{z_i}Q_i(z_i)=1,Q_i(z_i) \geq 0$
利用隐变量的概率分布，对原来的对数似然函数进行恒等变形。
根据随机变量函数的数学期望的定义可得：
把数学期望E看成是关于$Q_i(z_i)$概率的期望，由式（5.10）可得：
由式（5.10）、（5.11）可得：
式（5.12）为似然函数$\mathcal L(\theta)$下界函数，满足条件的下界函数有很多。因为EM是迭代算法，并且是求下界函数的极值点来找到下一步迭代的参数$\theta$，设$\theta_t$为第t次迭代时参数的估计值。
如何取在$\theta_t$处下界函数？当然与似然函数$\mathcal L(\theta)$越接近越好，所以我们希望(5.12)式在$\theta_t$ 这个点能取等号。由Jensen不等式可知，等式成立的条件是随机变量是常数，故在$\theta_t$点处有：
所以
由此可知，$Q_i(z_i)$实际上就是隐变量$z_i$的后验概率$p(z_i|x_i,\theta_t)$。
用$p(z_i|x_i,\theta_t)$表示$Q_i(z_i)$代入 $\mathcal L(\theta)$的下界函数中，得：
对$\mathcal L(\theta)$的下界函数中求极大值为下次迭代的参数值$?_{t+1}$,即有：
到这来EM算法的推导就结束了。

下面给出EM算法的具体步骤：
（1） 初始化参数$\theta_{0}$，然后开始循环迭代，第t次迭代的分为两步，即E步和M步。
（2） E步：
基于当前参数估计值$\theta_{t}$，构建目标函数。
具体包括计算给定样本时对隐变量z的条件概率，即
$Q_{it}(z_i)=p(z_i|x_i,\theta_t)\tag{5.13}$
然后计算$Q(\theta,\theta_t)$函数。
（3） M步
求$Q(\theta,\theta_t)$函数的极大值，更新参数为$\theta _{t+1}$.
$\theta_{t+1}= \underset{\theta}{argmax} Q(\theta,\theta_t)\tag{5.14}$
迭代第（2）和（3）步，直到参数$\theta _{t}$收敛或到指定的阈值。

5.3.3 EM算法简单实例

根据表2的情况可知，只要知道Z，就能求出参数$\theta=(p_1,p_2)$。但要知道Z，又必须通过参数$\theta$推导出来，否则无法推出z的具体情况。为此，我们可以把Z看成一个隐变量，这样完整的数据就是（X,Z），通过极大似然估计对参数$\theta=(p_1,p_2)$进行估计，因存在隐变量z，一般无法直接用解析式表达参数，故采用迭代的方法进行优化，具体步骤如下：
输出:模型参数$\theta$
EM算法具体步骤
（1）先初始化参数$\theta_0=(p_1^0,p_2^0)$
（2）假设第t次循环时参数为$\theta_t$，求Q函数
$Q(\theta,\theta_t)=\sum_{i=1}^m\sum_{z_i} p(z_i|x_i,\theta_t )logp(x_i,z_i|\theta)$
（3）对Q函数中的参数$\theta$实现极大似然估计，得到$\theta_{t+1}$
$\theta_{t+1}= \underset{\theta}{argmax} Q(\theta,\theta_t)$
（4）重复第（2）和（3）步，直到收敛或指定循环步数。
其中第（2）步需要求$\p(z_i|x_i,\theta_t )$,我们定义为：
根据这个迭代步骤，第1次迭代过程如下：
（1）初始化参数$\theta_0=(p_1^0,p_2^0)$
（2）E步，计算Q函数
先计算隐含变量的后验概率：$p(z_i|x_i,\theta_t )$

按同样方法，完成剩下4轮投掷，最后得到投掷统计信息如下表所示：
$\mu_i=p(z_i|x_i,\theta_t )$的实现过程可用二项分布的实现，具体过程如下：

计算Q函数，设$y_i$表示第i轮投掷出现正面的次数。
（3）对Q函数中的参数$\theta$实现极大似然估计，得到$\theta_1$
$\theta_{1}= \underset{\theta}{argmax} Q(\theta,\theta_0)$
对Q函数求导，并令导数为0。
所以$\theta_1=(0.35,0.53)$
进行第2轮迭代：
基于第1轮获取的参数$\theta_1=(0.35,0.53)$，进行第2轮EM计算：
计算每个实验中选择的硬币是1和2的概率，计算Q函数（E步），然后在计算M步，得$\theta_2=(0.40,0.48)$
继续迭代，直到收敛到指定阈值或循环次数。

以上计算过程可用Python实现

具体代入如下：
把硬币1用A表示，硬币1用B表示。H（或1）表示正面朝上，T（或0）表示反面朝上。
1、导入需要的库

2、把观察数据写成矩阵

3、单步EM算法，迭代一次算法实现步骤

4、执行

[0.35, 0.53]
与手工计算的结果一致。
5、EM算法主循环
EM算法的主循环，给定循环的两个终止条件：模型参数变化小于阈值；循环达到最大次数。

6、测试

运行结果
[[0.35, 0.53], 1]

运行结果
[0.4, 0.48], 2]

运行结果
[[0.44, 0.44], 5]

练习

用python实现以下这个简单实例：

5.3EM算法

EM (expectation-maximization)算法又称期望最大化算法,是Dempster, Laind, Rubin于1977年提出的求参数极大似然估计的一种迭代优化策略, 用于含有隐变量（Hidden variable）的概率模型参数的极大似然估计（或极大后验概率估计），它可以从非完整数据集中对参数进行极大似然估计,是一种非常简单实用的学习算法。
如果模型涉及的数据都是可观察数据，可以直接使用极大似然估计或极大后验概率估计的方法求解模型参数。但当模型有隐变量时，不能简单使用极大似然估计，需要迭代的方法，迭代一般分为两步：E步，求期望；M步，求极大值。
如何更好理解EM算法？这里有几个问题，理解这些问题有助理解EM算法。
本节将回答如下几个问题：
• 何为隐变量？如何理解隐变量？采用隐变量的概率分布与全概率公式中完备概率有何区别？
• 为何使用EM算法？为何通过迭代方法能不断靠近极值点？迭代结果是递增吗？
通过简单实例说明如何使用EM算法。
• EM算法的推导过程
• 为何选择q(z│x,θ)作为逼近分布？
• EM算法是一种方法或思想，EM有哪些使用场景。

5.3.1 何为隐变量？

在统计学中，随机变量，如$x_1=[1,3,7,4],x_2=[5,2,9,8]$等变量称为可观察的变量，与之相对的往往还有一些不可观测的随机变量，我们称之为隐变量或潜变量。隐变量可以通过使用数学模型依据观测得的数据被推断出来。
为了更好说明隐变量，我们先看一个简单实例。
现在有两枚硬币1和2，假设随机抛掷后正面朝上概率分别为$p_1,p_2$。为了估计这两个概率，做如下实验，每次取一枚硬币，连掷5次，记录下结果，这里每次试验的硬币为一随机变量，连掷5次，每次对应一个随机变量，详细信息如下：
表1—硬币投掷试验
从表1可知，这个模型的数据都是可观察数据，根据这个试验结果，不难算出硬币1和2正面朝上的概率：

从表1可知，每个实验选择的是硬币1还是硬币2，是可观察数据，如果把抛掷硬币1或2正面朝上的概率作为参数$\theta=(p_1,p_2 )$，也可以极大似然估计的方法得到。
这个通过求极大似然估计得到的参数与前面用通常计算频率的完全一致。
如果不告诉你每次投掷的是哪个硬币，或不知道每次投掷的是哪个硬币，此时，每次投掷的是哪个硬币就是一个无法观察的数据，这个数据我们通常称作为隐变量。用隐变量z表示没观察数据，其它各项不变。表1就变成表2的格式。表2—含隐含变量z的硬币投掷试验

5.3.2 EM算法

5.3.3 EM算法简单实例

5.3.4 EM算法推导

5.3.5 EM算法的收敛性

5.3.6从变分推断看EM算法

5.3.7 为何选择变分函数p(z│x,θ)作为逼近分布,而不是其它函数？

5.3.8 EM算法应用于k-means聚类

5.3.9 EM算法应用于高斯混合模型

5.3.10 EM算法核心思想

EM算法是一类算法，该算法核心是解决了带隐变量的参数估计。通过迭代的方法求参数的极大似然估计。具体步骤为：
（1）初始化参数$\theta_0$；
（2）构建含隐变量的目标函数,如$Q(\theta,\theta_t)$函数，或欧氏距离等。
（3）求目标函数的极值，得到参数$\theta_t$
重复第（2）和（3）步，直到收敛或指定迭代次数。
极大似然估计和EM算法，与其说是一种算法，不如说是一种解决的框架，如拉格朗日乘数法、蒙特卡洛算法等一样，针对特定场景的特定算法，和线性回归，逻辑回归，决策树等一些具体的算法不同，极大似然和EM算法更加宽泛，是很多具体算法的基础。

5.3.11 EM算法的应用场景

EM算法的应用场景，一般而言，就是处理含有隐变量的极大似然估计问题，具体可分为以下一些具体情况：
1、存在缺失数据：缺失数据包括类别标签或缺失某些特征的值等情况。
2、无监督学习：聚类：对个样本所属族作为隐变量
3、隐马尔科夫模型：训练隐马尔科夫模型中的参数
4、运用在语言模型上：对文本进行分类
5、生成模型（VAE,GAN等）中应用
6、Gibbs采样中应用

5.3.12 EM算法的推广