机器学习、深度学习的基础除了编程语言外,还有一个就是应用数学。它一般包括线性代数、概率与信息论、概率图、数值计算与最优化等。其中线性代数又是基础的基础。线性代数是数学的一个重要分支,广泛应用于科学和工程领域。大数据、人工智能的源数据在模型训练前,都需要转换为向量或矩阵,而这些运算正是线性代数的主要内容。
如在深度学习的图像处理中,如果1张图由28*28像素点构成,那这28*28就是一个矩阵。在深度学习的神经网络中,权重一般都是矩阵,我们经常把权重矩阵W与输入X相乘,输入X一般是向量,这就涉及矩阵与向量相乘的问题。诸如此类,向量或矩阵之间的运算在深度学习中非常普遍,也非常重要。
本章主要介绍如下内容:
标量、向量、矩阵和张量
矩阵和向量运算
特殊矩阵与向量
线性相关性及向量空间
3.1标量、向量、矩阵和张量
在机器学习、深度学习中,首先遇到的就是数据,如果按类别来划分,我们通常会遇到以下4种类型的数据。
1.标量(scalar)
一个标量就是一个单独的数,一般用小写的变量名称表示,如a,x等。
2.向量(vector)
向量就是一列数或一个一维数组,这些数是有序排列的。通过次序中的索引,我们可以确定向量中每个单独的数。通常我们赋予向量粗体的小写变量名称,如x、y等。一个向量一般有很多元素,这些元素如何表示?我们一般通过带脚标的斜体表示,如x_1 表示向量x中的第一个元素,x_2表示第二元素,依次类推。
当需要明确表示向量中的元素时,我们一般将元素排列成一个方括号包围的纵列:

我们可以把向量看作空间中的点,每个元素是不同的坐标轴上的坐标。
向量可以这样表示,那我们如何用编程语言如python来实现呢?如何表示一个向量?如何获取向量中每个元素呢?请看如下实例:
|
1 2 3 4 5 |
import numpy as np a=np.array([1,2,4,3,8]) print(a.size) print(a[0],a[1],a[2],a[-1]) |
打印结果如下:
5
1 2 4 8
这说明向量元素个数为5,向量中索引一般从0开始,如a[0]表示第一个元素1,a[1]
表示第二个元素2,a[2]表示第三个元素4,依次类推。这是从左到右的排列顺序,如果从右到左,我们可用负数来表示,如a[-1]表示第1个元素(注:从右到左),a[-2]表示第2个元素,依次类推。
3.矩阵(matrix)
矩阵是二维数组,其中的每一个元素被两个索引而非一个所确定。我们通常会赋予矩阵粗体的大写变量名称,比如A。如果一个实数矩阵高度为m,宽度为n,那么我们说A∈R^mxn。
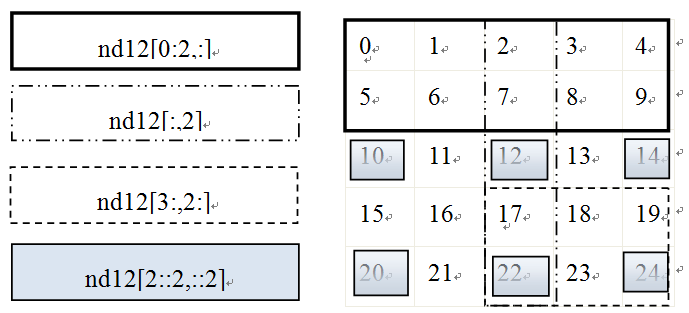
与向量类似,可以通过给定行和列的下标表示矩阵中元素,下标用逗号分隔,如A_1,1表示A左上的元素,A_1,2表示第一行第二列对应的元素,依次类推;这是表示单个元素,如果我们想表示1列或1行,该如何表示呢?我们可以引入冒号":"来表示,如第1行,可用A1,:表示,第2行,用A2,:表示,第1列用A:,1表示,第n列用A:,n表示。
如何用Python来表示或创建矩阵呢?如果希望获取其中某个元素,该如何实现呢?请看如下实例:
|
1 2 3 4 5 6 7 8 |
import numpy as np A=np.array([[1,2,3],[4,5,6]]) print(A) print(A.size) #显示矩阵元素总个数 print(A.shape) #显示矩阵现状,即行行和列数。 print(A[0,0],A[0,1],A[1,1]) print(A[1,:]) #打印矩阵第2行 |
打印结果:
[[1 2 3]
[4 5 6]]
6
(2, 3)
1 2 5
[4 5 6]
矩阵可以用嵌套向量生成,和向量一样,在Numpy中,矩阵元素的下标索引也是从0开始的。
4.张量(tensor)
几何代数中定义的张量是向量和矩阵的推广,通俗一点理解的话,我们可以将标量视为零阶张量,向量视为一阶张量,那么矩阵就是二阶张量,三阶的就称为三阶张量,以此类推。在机器学习、深度学习中经常遇到多维矩阵,如一张彩色图片就是一个三阶张量,三个维度分别是图片的高度、宽度和色彩数据。
张量(tensor)也是深度学习框架TensorFlow的重要概念。TensorFlow由tensor(张量)+flow(流)构成。
同样我们可以用Python来生成张量及获取其中某个元素或部分元素,请看实例:
|
1 2 3 4 5 6 |
B=np.arange(16).reshape((2, 2, 4)) #生成一个3阶矩阵 print(B) print(B.size) #显示矩阵元素总数 print(B.shape) #显示矩阵的维度 print(B[0,0,0],B[0,0,1],B[0,1,1]) print(B[0,1,:]) |
打印结果如下:
[[[ 0 1 2 3]
[ 4 5 6 7]]
[[ 8 9 10 11]
[12 13 14 15]]]
16
(2, 2, 4)
0 1 5
[4 5 6 7]
5.转置(transpose)
转置以主对角线(左上到右下)为轴进行镜像操作,通俗一点来说就是行列互换。将矩
向量可以看作只有一列的矩阵,把(3.1)式中向量x进行转置,得到下式。
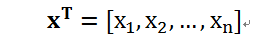
用Numpy如何实现张量的转置?很简单,利用张量的T属性即可,示例如下:
|
1 2 3 4 |
C=np.array([[1,2,3],[4,5,6]]) D=C.T #利用张量的T属性(即转置属性) print(C) print(D) |
打印结果如下:
[[1 2 3]
[4 5 6]]
[[1 4]
[2 5]
[3 6]]
3.2矩阵和向量运算
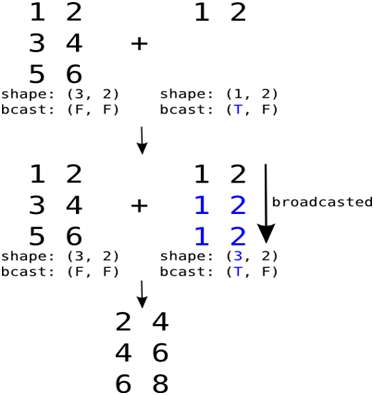
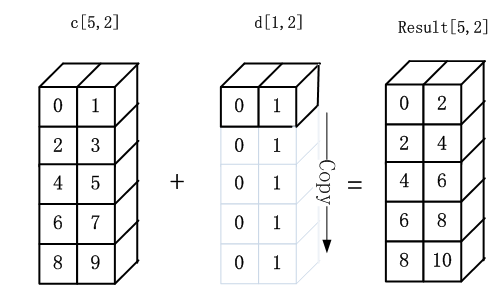
矩阵加法和乘法是矩阵运算中最常用的操作之一,两个矩阵相加,需要它们的形状相同,进行对应元素的相加,如:C=A+B,其中C_(i,j)=A_(i,j)+B_(i,j)。矩阵也可以和向量相加,只要它们的列数相同,相加的结果是矩阵每行与向量相加,这种隐式地复制向量b到很多位置的方式称为广播(broadcasting),以下我们通过一个代码实例来说明。
|
1 2 3 4 |
C=np.array([[1,2,3],[4,5,6]]) b=np.array([10,20,30]) D=C+b print(D) |
打印结果为:
[[11 22 33]
[14 25 36]]
两个矩阵相加,要求它们的形状相同,如果两个矩阵相乘,如A和B相乘,结果为矩阵C,矩阵A和B需要什么条件呢?条件比较简单,只要矩阵A的列数和矩阵B的行数相同即可。如果矩阵A的形状为m×n,矩阵B的形状为n×p,那么矩阵C的形状就是m×p,例如:
C=AB,则它们的具体乘法操作定义为:

矩阵乘积有很多重要性质,如满足分配律A(B+C)=AB+AC 和结合律,A(BC)=(AB)C。大家思考一下是否满足交换律?

3.3特殊矩阵与向量
上一节我们介绍了一般矩阵的运算,实际上在机器学习或深度学习中,我们还经常遇到一些特殊类型的矩阵,如可逆矩阵、对称矩阵、对角矩阵、单位矩阵、正交矩阵等等。这些特殊矩阵有特殊属性,下面我们逐一进行说明。
1.可逆矩阵
先简单介绍一下可逆矩阵,因后续需要用到。在(3.3)式中,假设矩阵W已知,向量b已知,如何求向量x?为求解向量x,我们需要引入一个称为逆矩阵的概念。而为了求逆矩阵,又牵涉到单位矩阵,何为单位矩阵?单位矩阵的结构很简单,就是所有沿主对角线上的元素都是1,而其他位置的元素都是0的方阵(行数等于列数的矩阵),一般记为I_n,如:

对此后续我们有更详细的讨论及代码实现。
2.对角矩阵
对角矩阵只有在主对角线上才有非零元素,其余都是0。从形式上来看,如果A为对角矩阵,当且仅当对所有i≠j,A_(i,j)=0。对角矩阵可以是方阵(行数等于列数)也可以不是方阵,如下矩阵,就是一个对角矩阵。
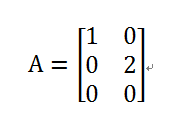
对角矩阵有非常好的性质,这些性质使很多计算非常高效,在机器学习、深度学习中经常会遇到对角矩阵。
对于对角矩阵为方阵的情况,我们可以把对角矩阵简单记为:

从上面两个式子可以看到对角矩阵的简洁高效。
(3)对称矩阵
对称矩阵,对于任意一个n阶方阵A,若A满足:A=A^T成立,则称方阵A为对称矩阵。
(4)单位向量

3.4线性相关性及向量空间
前面我们介绍了向量、矩阵等概念,接下来我们将介绍向量组、线性组合、线性相关性、秩等重要概念。
由多个同维度的列向量构成的集合称为向量组,矩阵可以看成是由行向量或列向量构成的向量组。
1.线性组合

2.线性相关

秩是一个重要概念,运用非常广泛,实际上矩阵我们可以看成是一个向量组。如果把矩阵看成是由所有行向量构成的向量组,这样矩阵的行秩就等于行向量组的秩;如果把矩阵看成是由所有列向量构成的向量组,这样矩阵的列秩就等于列向量组的秩。矩阵的行秩与列秩相等,因此,把矩阵的行秩和列秩统称为矩阵的秩。
3.5范数
数有大小,向量也有大小,向量的大小我们通过范数(Norm)来衡量。范数在机器学习、深度学习中运用非常广泛,特别在限制模型复杂度、提升模型的泛化能力方面效果不错。p范数的定义如下:


前面主要介绍了利用范数来度量向量的大小,矩阵的大小如何度量呢?我们可以用类似的方法。在深度学习中,常用Frobenius范数来描述,即:
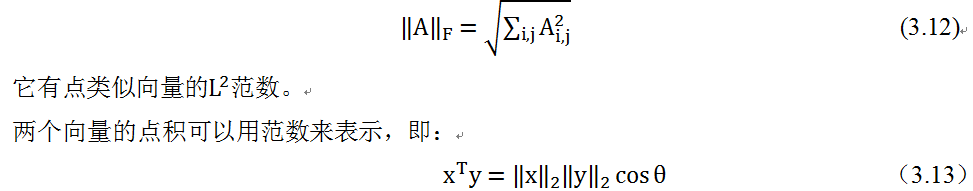
其中θ表示x与y之间的夹角。
以上说了向量一种度量方式,即通过范数来度量向量或矩阵的大小,并有具体公式,在实际编程中如何计算向量的范数呢?这里我们还是以Python为例进行说明。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import numpy as np import numpy.linalg as LA #导入Numpy中线性代数库 x=np.arange(0,1,0.1) #自动生成一个[0,1)间的10个数,步长为0.1 print(x) x1= LA.norm(x,1) #计算1范数 x2= LA.norm(x,2) #计算2范数 xa=LA.norm(x,np.inf) #计算无穷范数 print(x1) print(x2) print(xa) |
打印结果如下:
[ 0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]
4.5
1.68819430161
0.9
由此看出利用Python求向量的范数还是很方便的。
3.6特征值分解
许多数学对象可以分解成多个组成部分。特征分解就是使用最广的矩阵分解之一,即将矩阵分解成一组特征向量和特征值。本节讨论的矩阵都是方阵。
我们先介绍特征值、特征向量的概念。
设A是一个n阶方阵,如果存在实数⋋和n维的非零向量x,满足:
Ax=⋋x (3.14)
那么把数⋋称为方阵A的特征值,向量x称为矩阵A对应特征值⋋的特征向量。
假设矩阵A有n个线性无关的特征向量{ν^1,ν^2,⋯,ν^n},它们对应的特征值为{⋋_1,⋋_2,⋯,⋋_n}
把这n个线性无关的特征向量组合成一个新方阵,每一列是一个特征向量。
V=[ν^1,ν^2,⋯,ν^n]
用特征值构成一个n阶对角矩阵,对角线的元素都是特征值。
〖〖diag(λ)=[⋋〗_1,⋋_2,⋯,⋋_n]〗^T
那么,A的特征分解可表示为:
A=Vdiag(λ)V^(-1) (3.15)
注意,并不是所有方阵都能进行特征值分解,一个n阶方阵A能进行特征值分解的充分必要条件是它含有n个线性无关的特征向量。
这里我们介绍了给定一个方阵,如何求该方阵的特征向量和特征值?如何用编程语言实现?这些问题有了Python的帮忙,实现起来都非常简单,具体请看如下示例:
|
1 2 3 4 5 6 7 8 |
import numpy as np a = np.array([[1,2],[3,4]]) # 示例矩阵 A1 = np.linalg.eigvals(a) # 得到特征值 A2,V1 = np.linalg.eig(a) # 其中A2也是特征值,B为特征向量 print(A1) print(A2) print(V1) |
打印结果:
[-0.37228132 5.37228132]
[-0.37228132 5.37228132]
[[-0.82456484 -0.41597356]
[ 0.56576746 -0.90937671]]
【说明】
在numpy.linalg模块中:
eigvals() 计算矩阵的特征值
eig() 返回包含特征值和对应特征向量的元组
3.7奇异值分解
上节我们介绍了方阵的一种分解方式,如果矩阵不是方阵,是否能分解?如果能,该如何分解?这节我们介绍一种一般矩阵的分解方法,称为奇异值分解,这种方法应用非常广泛,如降维、推荐系统、数据压缩等等。
矩阵非常重要,所以其分解方法也非常重要,方法也比较多,除了特征分解法,还有一种分解矩阵的方法,被称为奇异值分解(SVD)。将矩阵分解为奇异向量和奇异值。通过奇异分解,我们会得到一些类似于特征分解的信息。然而,奇异分解有更广泛的应用。
每个实数矩阵都有一个奇异值分解,但不一定都有特征分解。例如,非方阵的矩阵就没有特征分解,这时我们只能使用奇异值分解。
奇异分解与特征分解类似,只不过这回我们将矩阵A分解成三个矩阵的乘积:
A=UDV^T (3.16)
假设A是一个m×n矩阵,那么U是一个m×m矩阵,D是一个m×n矩阵,V是一个n×n矩阵。这些矩阵每一个都拥有特殊的结构,其中U和V都是正交矩阵,D是对角矩阵(注意,D不一定是方阵)。对角矩阵D对角线上的元素被称为矩阵A的奇异值。矩阵U的列向量被称为左奇异向量,矩阵V 的列向量被称右奇异向量。
SVD最有用的一个性质可能是拓展矩阵求逆到非方矩阵上。奇异值分解,看起来很复杂,如果用python来实现,却非常简单,具体请看如下示例:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
import numpy as np Data=np.mat([[1,1,1,0,0], [2,2,2,0,0], [3,3,3,0,0], [5,5,3,2,2], [0,0,0,3,3], [0,0,0,6,6]]) u,sigma,vt=np.linalg.svd(Data) #print(u) print(sigma) #转换为对角矩阵 diagv=np.mat([[sigma[0],0,0],[0,sigma[1],0],[0,0,sigma[2]]]) print(diagv) #print(vt) |
打印结果:
[ 1.09824632e+01 8.79229347e+00 1.03974857e+00 1.18321522e-15
2.13044868e-32]
[[ 10.98246322 0. 0. ]
[ 0. 8.79229347 0. ]
[ 0. 0. 1.03974857]]
3.8迹运算
迹运算返回的是矩阵对角元素的和:
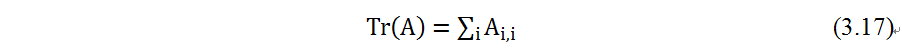
迹运算在某些场合非常有用。若不使用求和符号,有些矩阵运算很难描述,而通过矩阵乘法和迹运算符号可以清楚地表示。例如,迹运算提供了另一种描述矩阵Frobenius 范数的方式:

对迹运算的表达式,我们可以使用很多等式来表示。例如,迹运算在转置运算下是不变的:
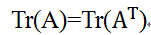
多个矩阵相乘得到的方阵的迹,和将这些矩阵中的最后一个挪到最前面之后相乘的迹是相同的。当然,我们需要考虑挪动之后矩阵乘积依然有定义:
Tr(ABC)=Tr(CAB)=Tr(BCA)
利用Python的Numpy对矩阵求迹同样方便。请看以下示例。
|
1 2 3 4 5 6 7 8 9 10 11 |
C=np.array([[1,2,3],[4,5,6],[7,8,9]]) TrC=np.trace(C) D=C-2 TrCT=np.trace(C.T) TrCD=np.trace(np.dot(C,D)) TrDC=np.trace(np.dot(D,C)) print(TrC) print(TrCT) print(TrCD) print(TrDC) |
打印结果:
15
15
171
171
3.9实例:Python实现主成分分析
主成分分析(Principal Component Analysis,PCA)是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
在许多机器学习、深度学习的应用中,往往需要处理大量样本或大的矩阵,多变量大样本无疑会为研究和应用提供丰富的信息,但也在一定程度上增加了数据采集的工作量。更重要的是在多数情况下,许多变量之间可能存在相关性,从而增加了问题分析的复杂性,同时对分析带来不便。如果分别对每个指标进行分析,分析往往是孤立的,而不是综合的。而盲目减少指标又会损失很多信息,且容易产生错误的结论。
因此需要找到一个合理有效的方法,在减少需要分析的指标或维度的同时,尽量减少原指标所含信息的损失,以达到对所收集数据进行全面分析的目的。由于各变量间存在一定的相关关系,因此有可能用较少的综合指标分别存在变量的各类信息。主成分分析就属于这类降维的方法。
如何实现以上目标呢?这里我们简要说明一下原理,然后使用Python来实现,至于详细的推导过程,大家可参考相关书籍或网上资料。
问题:设在n维空间中有m个样本点:{x^1,x^2,…,x^m},假设m比较大,需要对这些点进行压缩,使其投影到k为空间中,其中k<n,同时使损失的信息最小。
该如何实现呢?以下简要说明一下思路。

要使信息损失最小,一种合理的设想就是重构后的点X^*与原来的数据点之间距离最小,据此,PCA可转换为求带约束的最优化问题:

最后对(3.22)式两端对w求导,并令导数为0,化简后就可得到:
XX^T W=⋋W (3.23)
由(3.23)式可知,W是由协方差矩阵XX^T的特征向量构成的特征矩阵,利用特征值分解的方法就可求出W。
以下我们Python具体实现一个PCA实例。以iris为数据集,该数据集可以通过load_iris自动下载。
1)iris数据集简介:
Iris数据集是常用的分类实验数据集,由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集。数据集包含150个数据集,分为3类,每类50个数据,每个数据包含4个属性。可通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三类中的哪一类。
2)算法主要步骤为:
(1)对向量X进行去中心化
(2)计算向量X的协方差矩阵,自由度可以选择0或者1
(3)计算协方差矩阵的特征值和特征向量
(4)选取最大的k个特征值及其特征向量
(5)用X与特征向量相乘
3)代码实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
from sklearn.datasets import load_iris import numpy as np from numpy.linalg import eig def pca(X, k): # Standardize by remove average X = X - X.mean(axis = 0) # Calculate covariance matrix: X_cov = np.cov(X.T, ddof = 0) # Calculate eigenvalues and eigenvectors of covariance matrix eigenvalues, eigenvectors = eig(X_cov) # top k large eigenvectors klarge_index = eigenvalues.argsort()[-k:][::-1] k_eigenvectors = eigenvectors[klarge_index] return np.dot(X, k_eigenvectors.T) iris = load_iris() X = iris.data k = 2 #选取贡献最大的前2个特征 X_pca = pca(X, k) 4)我们看一下各特征值的贡献率 import numpy as np import seaborn as sns import matplotlib.pyplot as plt from sklearn.datasets import load_iris from numpy.linalg import eig %matplotlib inline iris = load_iris() X = iris.data X = X - X.mean(axis = 0) # 计算协方差矩阵 X_cov = np.cov(X.T, ddof = 0) #计算协方差矩阵的特征值和特征向量 eigenvalues, eigenvectors = eig(X_cov) tot=sum(eigenvalues) var_exp=[(i / tot) for i in sorted(eigenvalues,reverse=True)] cum_var_exp=np.cumsum(var_exp) plt.bar(range(1,5),var_exp,alpha=0.5,align='center',label='individual var') plt.step(range(1,5),cum_var_exp,where='mid',label='cumulative var') plt.ylabel('variance rtion') plt.xlabel('principal components') plt.legend(loc='best') plt.show() |
各特征值的贡献率如图3-1所示,可以看出,前2个特征值的方差贡献率超过95%,所以k取2有其合理性。
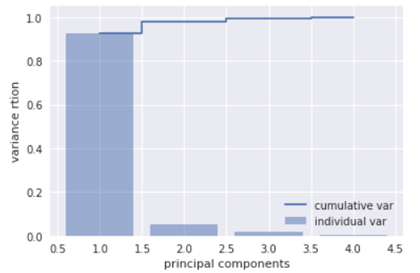
图3-1 各特征值的贡献率示意图
3.10小结
本章主要介绍线性代数中矩阵及向量有关概念,以及相关规则和运算等。线性代数是机器学习、深度学习的重要基础,与之相当的还有概率与信息论,我们将在下一章介绍。