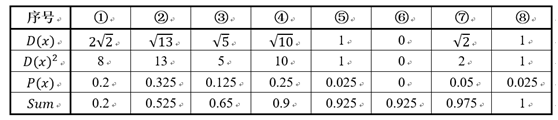
16.1 目的
回归分析(regression analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。运用十分广泛,回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且自变量之间存在线性相关,则称为多重线性回归分析.
16.2 模型
16.3 问题
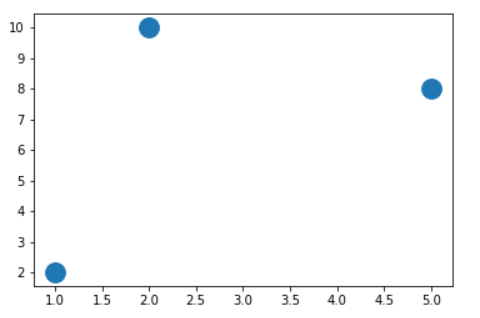
假设我们有一组某企业广告费与销售额之间的对应关系的实际数据: 对这些数据可视化结果如下:
对这些数据可视化结果如下:
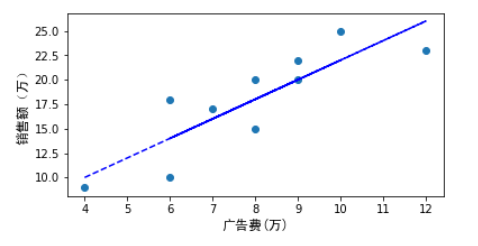
可视化代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import matplotlib.pyplot as plt import matplotlib.font_manager as fm myfont = fm.FontProperties(fname='/home/hadoop/anaconda3/lib/python3.6/site-packages/matplotlib/mpl-data/fonts/ttf/simhei.ttf') x=[4,8,9,8,7,12,6,10,6,9] y=[9,20,22,15,17,23,18,25,10,20] #y1=[10,18,20,18,16,26,14,22,14,20] #y=2x+2 plt.figure(figsize=(6,3)) plt.scatter(x,y) #plt.plot(x,y1,color='blue',linestyle='dashed') plt.xlabel("广告费(万)",fontproperties=myfont,size=12) plt.ylabel("销售额(万)",fontproperties=myfont,size=12) plt.show() |
如果该企业先增加广告费,如20万,那么它可能带来的销售额大概是多少?
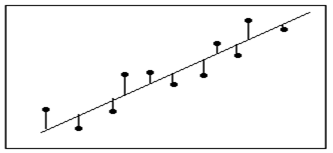
解决这个问题的关键就是如何根据已有数据的总体趋势,拟合出一条直线,如图1.1中虚线所示,那么新给出的广告费就可预测其对应的销售额?如何拟合这条直线呢?
16.4 简单入手
假设我们要拟合的这条直线为一元一次直线,表达式为:
y=ax+b (1.1)
要拟合这条直线或确定这条直线,只要求出a和b即可。那如何得到a和b呢?
这条直线要满足什么条件才是最好的或最能体现这些样本的趋势?
如果能使预测值与实际值的差距最小,应该是一个不错的直线。
由此,想到最小二乘法,利用最小二乘法作为损失函数,然后通过使损失函数最小化来求参数a和b。
最损失函数的最小值,而且损失函数为凸函数,故可利用梯度为0来求出参数a和b
具体过程如下:


如此,a,b确定后,自然直线y=ax+b也就确定了,这样便可以根据新的x值,预测其y值了。
16.5、用Python解方程求出a和b
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
#根据y=ax+b随意写几个数 X=[4,8,9,8,7,12,6,10,6,9] Y=[9,20,22,15,17,23,18,25,10,20] #初始化以下序列 Xsum=0.0 X2sum=0.0 Ysum=0.0 XY=0.0 #得到序列元素个数或长度 n=len(X) for i in range(n): Xsum+=X[i] Ysum+=Y[i] XY+=X[i]*Y[i] X2sum+=X[i]**2 a=(n*XY-Xsum*Ysum)/( n*X2sum-Xsum**2) b=(Ysum-a*Xsum)/n print('所求直线为: y=%f*x+%f' % (a,b) ) |
打印结果为:
所求直线为: y=1.980810*x+2.251599
16.6 用迭代方式求参数
以下利用迭代的方法求出参数a和b
直接通过解方程来求参数a和b,如果参数比较多,样本数也很多的情况下,计算量非常大,而且也不现实。因此,我们需要另辟蹊径!
还是以求函数y=x^2的最小值为例,我们可以通过其导数为0来求来求的是y最小的x值;我们也可以通过迭代的方式来求,先从某点开始,如x_0开始,然后沿梯度的方向,不断靠近最小值点,如下图所示:
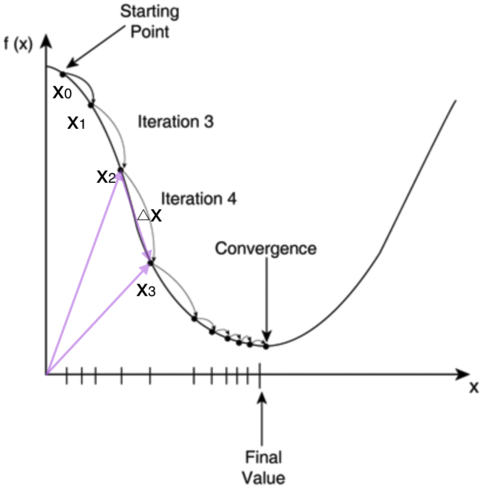

为啥每次修改的值,都能往函数最小值那个方向前进呢?这里的奥秘在于,我们每次都是向函数的梯度的相反方向来修改。
什么是梯度呢?翻开大学高数课的课本,我们会发现梯度是一个向量,它指向函数值上升最快的方向。显然,梯度的反方向当然就是函数值下降最快的方向了。我们每次沿着梯度相反方向去修改的值,当然就能走到函数的最小值附近。
之所以是最小值附近而不是最小值那个点,是因为我们每次移动的步长不会那么恰到好处,有可能最后一次迭代走远了越过了最小值那个点。步长的选择是门手艺,如果选择小了,那么就会迭代很多轮才能走到最小值附近;如果选择大了,那可能就会越过最小值很远,收敛不到一个好的点上。
按照上面的讨论,我们就可以写出梯度下降算法的公式

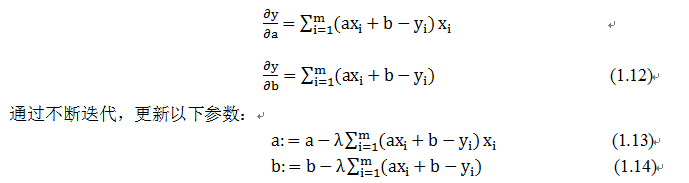
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
X=[4,8,9,8,7,12,6,10,6,9] Y=[9,20,22,15,17,23,18,25,10,20] #初始化参数a、b b=0.1 a=0.2 #alpha是学习率,代表的是迭代的步长 alpha=0.001 #定义线性模型函数 def h(i): return b+a*X[i] def diff(i): return h(i)-Y[i] #times 表示迭代1000次,那么基本上可以下降到梯度的最小值了 #每次迭代做的事情,就是式(1.13)、(1.14)两个公式,不停的去修改参数a,b for times in range(1000): sum1=0 sum2=0 for i in range(m): sum1=sum1+diff(i) sum2=sum2+diff(i)*X[i] b=b-alpha*sum1 a=a-alpha*sum2 print ("参数b的值:%.2f"%b) print ("参数a的值:%.2f"%a) |
打印结果:
参数b的值:2.44
参数a的值:1.95
通过迭代方法求得的参数a,b与通过梯度求得的参数进行比较,发现他们非常接近,有异曲同工之妙!
这种方法也可看作只有一个神经元的神经网络,并且没有激活函数的这种。
16.7 迭代中用矩阵代替循环
这里利用梯度下降更新参数时采用一个循环,循环一般比较耗费资源,如果有一千万个数据,将需要循环一千万次,这是不可接受的,那么我们是否能不用循环?
当然可以,如果用采用矩阵方式,需要进行如下操作:
把输入X,Y变为矩阵;
把模型变为矩阵或向量;
把式(1.13)变为矩阵与向量的点乘
把式(1.14)变为矩阵的累加
具体代码实现如下:
(1)定义一个线性回归类,在这个类中初始化两个参数,并定义几个函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
class LinearRegressGD(object): def __init__(self,eta=0.001,n_iter=4000): self.eta=eta self.n_iter=n_iter def fit(self,X,Y): #初始化参数 self.w=np.zeros(1+X.shape[1]) self.w[0]=0.1 self.w[1]=0.2 self.cost=[] #开始迭代循环 for i in range(self.n_iter): output=self.net_input(X) errors=(Y-output) self.w[1] +=self.eta*X.T.dot(errors) self.w[0] +=self.eta*(errors).sum() cost1=(errors**2).sum()/2.0 self.cost.append(cost1) return self def net_input(self,X): return np.dot(X,self.w[1])+self.w[0] def predict(self,X): return self.net_input(X) |
(2)把输入变为10x1矩阵,如何运行以上函数
|
1 2 3 4 5 6 7 |
import numpy as np X=np.array([4,8,9,8,7,12,6,10,6,9]).reshape(10,1) Y=np.array([9,20,22,15,17,23,18,25,10,20]).reshape(10,1) lr=LinearRegressGD() lr.fit(X,Y) print("参数a的值:%.3f"%lr.w[1]) print("参数b的值:%.3f"%lr.w[0]) |
打印结果:
参数a的值:1.995
参数b的值:2.130
(3)把迭代过程可视化
|
1 2 3 4 5 |
import matplotlib.pyplot as plt plt.plot(range(1,lr.n_iter+1),lr.cost) plt.ylabel('SSE') plt.xlabel('Epoch') plt.show() |
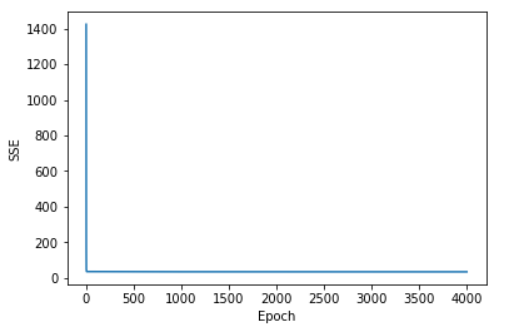
16.8 用Tensorflow架构实现自动求导,求参数
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
import numpy as np import tensorflow as tf #导入tensorflow import matplotlib.pyplot as plt # import matplotlib %matplotlib inline ##构造训练数据## x_data=np.array([4,8,9,8,7,12,6,10,6,9]) y_data=np.array([9,20,22,15,17,23,18,25,10,20]) #可视化 plt.figure() # Create a new figure plt.scatter(x_data,y_data) #Plot a scatter draw of the random datapoints plt.plot (x_data, 2.0 + 2.0 * x_data) # Draw one line with the line function ##初始化权重变量# w=tf.Variable(tf.random_uniform([1],-1.0,1.0)) b=tf.Variable(tf.zeros([1])) y=w*x_data+b ##计算损失函数 loss=tf.reduce_mean(tf.square(y-y_data)) #判断与正确值的差距 optimizer=tf.train.GradientDescentOptimizer(0.01) #根据差距进行反向传播修正参数 train=optimizer.minimize(loss) #建立训练器 init=tf.global_variables_initializer() #初始化TensorFlow训练结构 sess=tf.Session() #建立TensorFlow训练会话 #sess = tf.InteractiveSession() sess.run(init) #将训练结构装载到会话中 print('初始权重值w:',w.eval(session=sess)) for step in range(1000): #循环训练100次 sess.run(train) #使用训练器根据训练结构进行训练 if step%100==0: #每20次打印一次训练结果 print(step,sess.run(w),sess.run(b)) #训练次数,W值,b值 print(sess.run(loss)) print('最后权重值w:',w.eval(session=sess)) print('最后偏移量b:',b.eval(session=sess)) #可视化预测直线 plt.figure() # Create a new figure plt.scatter(x_data,y_data) plt.plot (x_data, sess.run(b) + x_data * sess.run(w)) |
运行结果
初始权重值w: [-0.99174666]
0 [ 3.35317731] [ 0.51469594]
100 [ 2.17306757] [ 0.62030703]
200 [ 2.14828968] [ 0.83054471]
300 [ 2.12670541] [ 1.01368761]
400 [ 2.10790277] [ 1.17322707]
500 [ 2.09152317] [ 1.31220567]
600 [ 2.07725477] [ 1.43327284]
700 [ 2.06482506] [ 1.53873765]
800 [ 2.05399752] [ 1.63060951]
900 [ 2.0445652] [ 1.71064162]
6.90384
最后权重值w: [ 2.03642535]
最后偏移量b: [ 1.77970874]
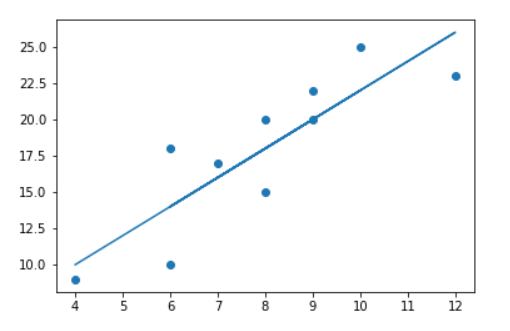
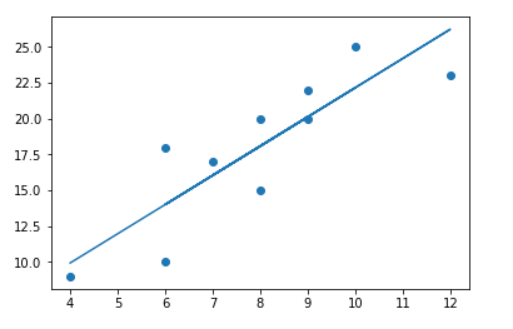
16.9 拓展