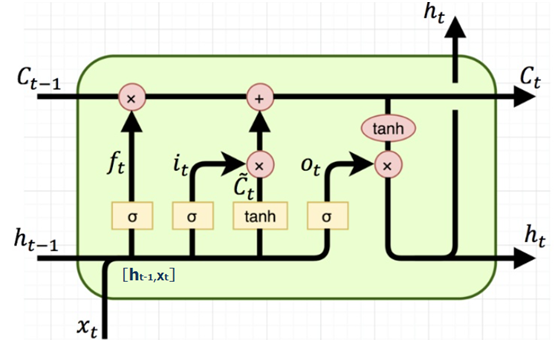
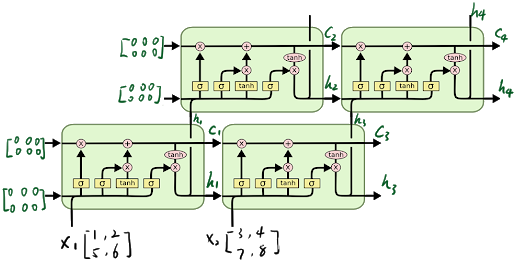
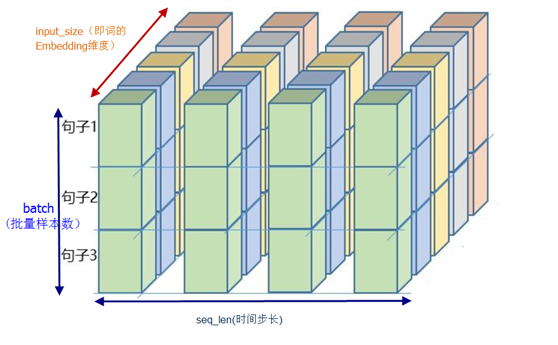
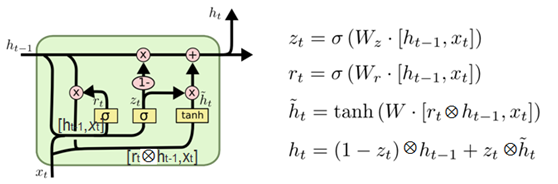
第1章 NumPy基础
在机器学习和深度学习中,图像、声音、文本等输入数据最终都要转换为数组或矩阵。如何有效进行数组和矩阵的运算?这就需要充分利用NumPy。NumPy是数据科学的通用语言,而且与Pytorch关系非常密切,它是科学计算、深度学习的基石。尤其对Pytorch而言,其重要性更加明显。Pytorch中的Tensor与NumPy非常相似,它们之间可以非常方便地进行转换,掌握NumPy是学好Pytorch的重要基础,故我们把它列为全书第1章。
为什么是NumPy?实际上Python本身含有列表(list)和数组(array),但对于大数据来说,这些结构有很多不足。因列表的元素可以是任何对象,因此列表中所保存的是对象的指针。例如为了保存一个简单的[1,2,3],都需要有3个指针和三个整数对象。对于数值运算来说这种结构显然比较浪费内存和CPU等宝贵资源。 至于array对象,它直接保存数值,和C语言的一维数组比较类似。但是由于它不支持多维,在上面的函数也不多,因此也不适合做数值运算。
NumPy(Numerical Python 的简称)的诞生弥补了这些不足,NumPy提供了两种基本的对象:ndarray(N-dimensional array object)和 ufunc(universal function object)。ndarray是存储单一数据类型的多维数组,而ufunc则是能够对数组进行处理的函数。
NumPy的主要特点:
(1)ndarray,快速和节省空间的多维数组,提供数组化的算术运算和高级的广播功能。
(2)使用标准数学函数对整个数组的数据进行快速运算,而不需要编写循环。
(3)读取/写入磁盘上的阵列数据和操作存储器映像文件的工具。
(4)线性代数,随机数生成,和傅里叶变换的能力。
(5)集成C,C++,Fortran代码的工具。
本章主要内容如下:
如何生成NumPy数组
如何存取元素
NumPy的算术运算
数组变形
批量处理
NumPy的通用函数
NumPy的广播机制
1.1 生成NumPy数组
NumPy是Python的外部库,不在标准库中。因此,若要使用它,需要先导入NumPy。
|
1 |
import numpy as np |
导入NumPy后,可通过np.+Tab键,查看可使用的函数,如果对其中一些函数的使用不很清楚,还可以在对应函数+?,再运行,就可很方便的看到如何使用函数的帮助信息。
np.然后按'Tab'键,将出现如下界面:
运行如下命令,便可查看函数abs的详细帮助信息。
|
1 |
np.abs? |
NumPy不但强大,而且还非常友好。
接下来我们将介绍NumPy的一些常用方法,尤其是与机器学习、深度学习相关的一些内容。
NumPy封装了一个新的数据类型ndarray(n-dimensional array),它是一个多维数组对象。该对象封装了许多常用的数学运算函数,方便我们做数据处理、数据分析等。如何生成ndarray呢?这里我们介绍生成ndarray的几种方式,如从已有数据中创建、利用random创建、创建特殊多维数组、使用arange函数等。
1.1.1 从已有数据中创建数组
直接对 Python 的基础数据类型(如列表、元组等) 进行转换来生成 ndarray:
(1)将列表转换成 ndarray
|
1 2 3 4 5 6 7 8 |
import numpy as np lst1 = [3.14, 2.17, 0, 1, 2] nd1 =np.array(lst1) print(nd1) # [3.14 2.17 0. 1. 2. ] print(type(nd1)) # <class 'numpy.ndarray'> |
(2)嵌套列表可以转换成多维 ndarray
|
1 2 3 4 5 6 7 8 9 |
import numpy as np lst2 = [[3.14, 2.17, 0, 1, 2], [1, 2, 3, 4, 5]] nd2 =np.array(lst2) print(nd2) # [[3.14 2.17 0. 1. 2. ] # [1. 2. 3. 4. 5. ]] print(type(nd2)) # <class 'numpy.ndarray'> |
如果把上面示例中的列表换成元组也同样适合。
1.1.2 利用 random 模块生成数组
在深度学习中,我们经常需要对一些参数进行初始化,为了更有效训练模型,提高模型的性能,有些初始化还需要满足一定条件,如满足正态分布或均匀分布等。这里我们介绍几种常用的方法,表1-1列举了 np.random 模块常用的函数。
表1-1 np.random模块常用函数

下面我们来看看一些函数的具体使用:
|
1 2 3 4 5 6 7 8 9 |
import numpy as np nd3 =np.random.random([3, 3]) print(nd3) # [[0.43007219 0.87135582 0.45327073] # [0.7929617 0.06584697 0.82896613] # [0.62518386 0.70709239 0.75959122]] print("nd3的形状为:",nd3.shape) # nd3的形状为: (3, 3) |
为了每次生成同一份数据,可以指定一个随机种子,使用shuffle函数打乱生成的随机数。
|
1 2 3 4 5 6 7 8 9 |
import numpy as np np.random.seed(123) nd4 = np.random.randn(2,3) print(nd4) np.random.shuffle(nd4) print("随机打乱后数据:") print(nd4) print(type(nd4)) |
输出结果:
[[-1.0856306 0.99734545 0.2829785 ]
[-1.50629471 -0.57860025 1.65143654]]
随机打乱后数据:
[[-1.50629471 -0.57860025 1.65143654]
[-1.0856306 0.99734545 0.2829785 ]]
1.1.3 创建特定形状的多维数组
参数初始化时,有时需要生成一些特殊矩阵,如全是 0 或 1 的数组或矩阵,这时我们可以利用np.zeros、np.ones、np.diag来实现,如表1-2所示。
表1-2 NumPy 数组创建函数

下面我们通过几个示例来说明:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
import numpy as np # 生成全是 0 的 3x3 矩阵 nd5 =np.zeros([3, 3]) #生成与nd5形状一样的全0矩阵 #np.zeros_like(nd5) # 生成全是 1 的 3x3 矩阵 nd6 = np.ones([3, 3]) # 生成 3 阶的单位矩阵 nd7 = np.eye(3) # 生成 3 阶对角矩阵 nd8 = np.diag([1, 2, 3]) print(nd5) # [[0. 0. 0.] # [0. 0. 0.] # [0. 0. 0.]] print(nd6) # [[1. 1. 1.] # [1. 1. 1.] # [1. 1. 1.]] print(nd7) # [[1. 0. 0.] # [0. 1. 0.] # [0. 0. 1.]] print(nd8) # [[1 0 0] # [0 2 0] # [0 0 3]] |
有时我们可能需要把生成的数据暂时保存起来,以备后续使用。
|
1 2 3 4 5 6 |
import numpy as np nd9 =np.random.random([5, 5]) np.savetxt(X=nd9, fname='./test1.txt') nd10 = np.loadtxt('./test1.txt') print(nd10) |
输出结果:
[[0.41092437 0.5796943 0.13995076 0.40101756 0.62731701]
[0.32415089 0.24475928 0.69475518 0.5939024 0.63179202]
[0.44025718 0.08372648 0.71233018 0.42786349 0.2977805 ]
[0.49208478 0.74029639 0.35772892 0.41720995 0.65472131]
[0.37380143 0.23451288 0.98799529 0.76599595 0.77700444]]
1.1.4 利用 arange、linspace 函数生成数组
arange 是 numpy 模块中的函数,其格式为:
|
1 |
arange([start,] stop[,step,], dtype=None) |
其中start 与 stop 指定范围,step 设定步长,生成一个 ndarray,start 默认为 0,步长 step 可为小数。Python有个内置函数range功能与此类似。
|
1 2 3 4 5 6 7 8 9 10 |
import numpy as np print(np.arange(10)) # [0 1 2 3 4 5 6 7 8 9] print(np.arange(0, 10)) # [0 1 2 3 4 5 6 7 8 9] print(np.arange(1, 4, 0.5)) # [1. 1.5 2. 2.5 3. 3.5] print(np.arange(9, -1, -1)) # [9 8 7 6 5 4 3 2 1 0] |
linspace 也是 numpy 模块中常用的函数,其格式为:
|
1 |
np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None) |
它可以根据输入的指定数据范围以及等份数量,自动生成一个线性等分向量,其中endpoint (包含终点)默认为 True,等分数量num默认为 50。如果将retstep设置为 True,则会返回一个带步长的 ndarray。
|
1 2 3 4 5 |
import numpy as np print(np.linspace(0, 1, 10)) #[0. 0.11111111 0.22222222 0.33333333 0.44444444 0.55555556 # 0.66666667 0.77777778 0.88888889 1. ] |
值得一提的,这里并没有像我们预期的那样,生成 0.1, 0.2, ... 1.0 这样步长为0.1的 ndarray,这是因为 linspace 必定会包含数据起点和终点,那么其步长则为(1-0) / 9 = 0.11111111。如果需要产生 0.1, 0.2, ... 1.0 这样的数据,只需要将数据起点 0 修改为 0.1 即可。
除了上面介绍到的 arange 和 linspace,NumPy还提供了 logspace 函数,该函数使用方法与 linspace 使用方法一样,读者不妨自己动手试一下。
1.2 获取元素
上节我们介绍了生成ndarray的几种方法,数据生成后,如何读取我们需要的数据?这节我们介绍几种常用方法。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import numpy as np np.random.seed(2019) nd11 = np.random.random([10]) #获取指定位置的数据,获取第4个元素 nd11[3] #截取一段数据 nd11[3:6] #截取固定间隔数据 nd11[1:6:2] #倒序取数 nd11[::-2] #截取一个多维数组的一个区域内数据 nd12=np.arange(25).reshape([5,5]) nd12[1:3,1:3] #截取一个多维数组中,数值在一个值域之内的数据 nd12[(nd12>3)&(nd12<10)] #截取多维数组中,指定的行,如读取第2,3行 nd12[[1,2]] #或nd12[1:3,:] ##截取多维数组中,指定的列,如读取第2,3列 nd12[:,1:3] |
如果对上面这些获取方式还不是很清楚,没关系,下面我们通过图形的方式进一步说明,如图1-1所示,左边为表达式,右边为表达式获取的元素。注意不同的边界,表示不同的表达式。
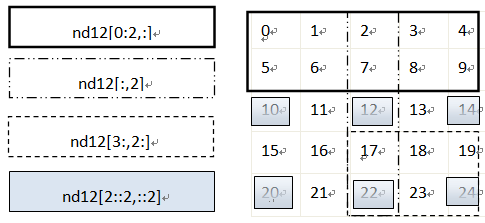
图1-1 获取多维数组中的元素
获取数组中的部分元素除通过指定索引标签外,还可以使用一些函数来实现,如通过random.choice函数可以从指定的样本中进行随机抽取数据。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np from numpy import random as nr a=np.arange(1,25,dtype=float) c1=nr.choice(a,size=(3,4)) #size指定输出数组形状 c2=nr.choice(a,size=(3,4),replace=False) #replace缺省为True,即可重复抽取。 #下式中参数p指定每个元素对应的抽取概率,缺省为每个元素被抽取的概率相同。 c3=nr.choice(a,size=(3,4),p=a / np.sum(a)) print("随机可重复抽取") print(c1) print("随机但不重复抽取") print(c2) print("随机但按制度概率抽取") print(c3) |
打印结果:
随机可重复抽取
[[ 7. 22. 19. 21.]
[ 7. 5. 5. 5.]
[ 7. 9. 22. 12.]]
随机但不重复抽取
[[ 21. 9. 15. 4.]
[ 23. 2. 3. 7.]
[ 13. 5. 6. 1.]]
随机但按制度概率抽取
[[ 15. 19. 24. 8.]
[ 5. 22. 5. 14.]
[ 3. 22. 13. 17.]]
1.3 NumPy的算术运算
在机器学习和深度学习中,涉及大量的数组或矩阵运算,这节我们重点介绍两种常用的运算。一种是对应元素相乘,又称为逐元乘法(element-wise product),运算符为np.multiply(), 或 *。另一种是点积或内积元素,运算符为np.dot()。
1.3.1对应元素相乘
对应元素相乘(element-wise product)是两个矩阵中对应元素乘积。np.multiply 函数用于数组或矩阵对应元素相乘,输出与相乘数组或矩阵的大小一致,其格式如下:
|
1 |
numpy.multiply(x1, x2, /, out=None, *, where=True,casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj]) |
其中x1,x2之间的对应元素相乘遵守广播规则,NumPy的广播规则本章第7小节将介绍。以下我们通过一些示例来进一步说明。
|
1 2 3 4 5 6 7 8 9 10 11 |
A = np.array([[1, 2], [-1, 4]]) B = np.array([[2, 0], [3, 4]]) A*B ##结果如下: array([[ 2, 0], [-3, 16]]) #或另一种表示方法 np.multiply(A,B) #运算结果也是 array([[ 2, 0], [-3, 16]]) |
矩阵A和B的对应元素相乘,用图1-2直观表示为:
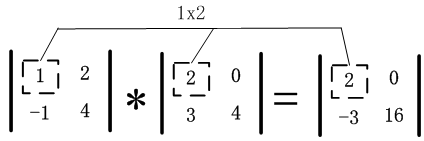
图1-2 对应元素相乘示意图
NumPy数组不仅可以和数组进行对应元素相乘,也可以和单一数值(或称为标量)进行运算。运算时,NumPy数组每个元素和标量进行运算,其间会用到广播机制(1.7小节将详细介绍)。
|
1 2 |
print(A*2.0) print(A/2.0) |
[[ 2. 4.]
[-2. 8.]]
[[ 0.5 1. ]
[-0.5 2. ]]
由此,推而广之,数组通过一些激活函数后,输出与输入形状一致。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
X=np.random.rand(2,3) def softmoid(x): return 1/(1+np.exp(-x)) def relu(x): return np.maximum(0,x) def softmax(x): return np.exp(x)/np.sum(np.exp(x)) print("输入参数X的形状:",X.shape) print("激活函数softmoid输出形状:",softmoid(X).shape) print("激活函数relu输出形状:",relu(X).shape) print("激活函数softmax输出形状:",softmax(X).shape) |
输入参数X的形状: (2, 3)
激活函数softmoid输出形状: (2, 3)
激活函数relu输出形状: (2, 3)
激活函数softmax输出形状: (2, 3)
1.3.2 点积运算
点积运算(dot product)又称为内积,在NumPy用np.dot表示,其一般格式为:
|
1 |
numpy.dot(a, b, out=None) |
以下通过一个示例来说明dot的具体使用及注意事项。
|
1 2 3 4 |
X1=np.array([[1,2],[3,4]]) X2=np.array([[5,6,7],[8,9,10]]) X3=np.dot(X1,X2) print(X3) |
[[21 24 27]
[47 54 61]]
以上运算,用图1-3可表示为:
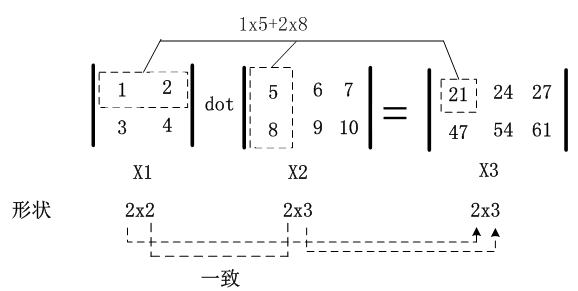
图1-3 矩阵的点积示意图,对应维度的元素个数需要保持一致
如图1-3所示,矩阵X1和矩阵X2进行点积运算,其中X1和X2对应维度(即X1的第2个维度与X2的第1个维度)的元素个数必须保持一致,此外,矩阵X3的形状是由矩阵X1的行数与矩阵X2的列数构成的。
1.4 数组变形
在机器学习以及深度学习的任务中,通常需要将处理好的数据以模型能接受的格式喂给模型,然后模型通过一系列的运算,最终返回一个处理结果。然而,由于不同模型所接受的输入格式不一样,往往需要先对其进行一系列的变形和运算,从而将数据处理成符合模型要求的格式。最常见的是矩阵或者数组的运算,经常会遇到需要把多个向量或矩阵按某轴方向合并,或需要展平(如在卷积或循环神经网络中,在全连接层之前,需要把矩阵展平)。下面介绍几种常用数据变形方法。
1.4.1 更改数组的形状
修改指定数组的形状是 NumPy 中最常见的操作之一,常见的方法有很多,表1-3 列出了一些常用函数。
表1-3 NumPy中改变向量形状的一些函数
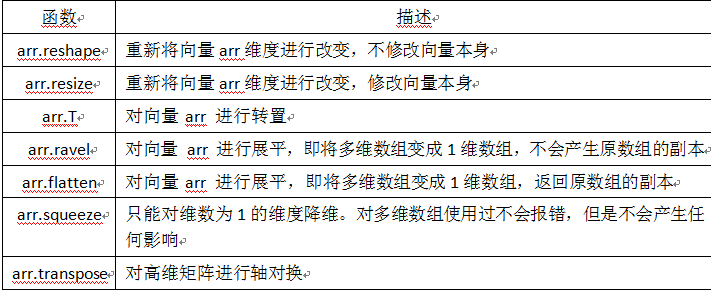
下面我们来看一些示例:
(1)reshape
|
1 2 3 4 5 6 7 8 9 |
import numpy as np arr =np.arange(10) print(arr) # 将向量 arr 维度变换为2行5列 print(arr.reshape(2, 5)) # 指定维度时可以只指定行数或列数, 其他用 -1 代替 print(arr.reshape(5, -1)) print(arr.reshape(-1, 5)) |
输出结果:
[0 1 2 3 4 5 6 7 8 9]
[[0 1 2 3 4]
[5 6 7 8 9]]
[[0 1]
[2 3]
[4 5]
[6 7]
[8 9]]
[[0 1 2 3 4]
[5 6 7 8 9]]
值得注意的是,reshape 函数支持只指定行数或列数,剩余的设置为-1即可。所指定的行数或列数一定要能被整除(如10不能被3整除),例如上面代码如果修改为arr.reshape(3,-1)将报错误。
(2)resize
|
1 2 3 4 5 6 7 |
import numpy as np arr =np.arange(10) print(arr) # 将向量 arr 维度变换为2行5列 arr.resize(2, 5) print(arr) |
输出结果:
[0 1 2 3 4 5 6 7 8 9]
[[0 1 2 3 4]
[5 6 7 8 9]]
(3).T
|
1 2 3 4 5 6 7 |
import numpy as np arr =np.arange(12).reshape(3,4) # 向量 arr 为3行4列 print(arr) # 将向量 arr 进行转置为4行3列 print(arr.T) |
输出结果:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[ 0 4 8]
[ 1 5 9]
[ 2 6 10]
[ 3 7 11]]
(4)ravel
|
1 2 3 4 5 6 7 8 9 10 |
import numpy as np arr =np.arange(6).reshape(2, -1) print(arr) # 按照列优先,展平 print("按照列优先,展平") print(arr.ravel('F')) # 按照行优先,展平 print("按照行优先,展平") print(arr.ravel()) |
输出结果:
[[0 1 2]
[3 4 5]]
按照列优先,展平
[0 3 1 4 2 5]
按照行优先,展平
[0 1 2 3 4 5]
(5)flatten
把矩阵转换为向量,这种需求经常出现在卷积网络与全连接层之间。
|
1 2 3 4 |
import numpy as np a =np.floor(10*np.random.random((3,4))) print(a) print(a.flatten()) |
输出结果:
[[4. 0. 8. 5.]
[1. 0. 4. 8.]
[8. 2. 3. 7.]]
[4. 0. 8. 5. 1. 0. 4. 8. 8. 2. 3. 7.]
(6)squeeze
这是一个重要用来降维的函数,把矩阵中含1的维度去掉。在Pytorch中还有一种与之相反的操作,torch.unsqueeze这个后面将介绍。
|
1 2 3 4 5 6 7 8 |
import numpy as np arr =np.arange(3).reshape(3, 1) print(arr.shape) #(3,1) print(arr.squeeze().shape) #(3,) arr1 =np.arange(6).reshape(3,1,2,1) print(arr1.shape) #(3, 1, 2, 1) print(arr1.squeeze().shape) #(3, 2) |
(7)transpose
对高维矩阵进行轴对换,这个在深度学习中经常使用,比如把图片表示颜色的RGB顺序,改为GBR的顺序。
|
1 2 3 4 5 |
import numpy as np arr2 = np.arange(24).reshape(2,3,4) print(arr2.shape) #(2, 3, 4) print(arr2.transpose(1,2,0).shape) #(3, 4, 2) |
1.4.2 合并数组
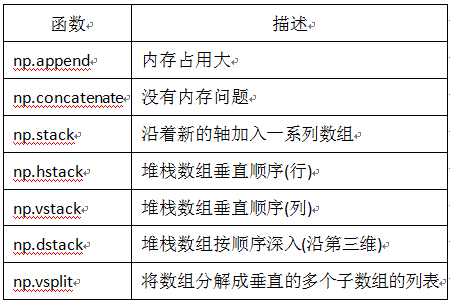
合并数组也是最常见的操作之一,表1-4列举了常用的用于数组或向量合并的方法。
表1-4 NumPy 数组合并方法
[说明]
①append、concatnate以及stack都有一个 axis 参数,用于控制数组合并是按行还是按列。
②对于append和concatnate,待合并的数组必须有相同的行数或列数(满足一个即可)。
③stack、hstack、dstack待合并的数组必须具有相同的形状( shape)。
下面选择一些常用函数进行说明。
(1)append
合并一维数组
|
1 2 3 4 5 6 7 |
import numpy as np a =np.array([1, 2, 3]) b = np.array([4, 5, 6]) c = np.append(a, b) print(c) # [1 2 3 4 5 6] |
合并多维数组
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np a =np.arange(4).reshape(2, 2) b = np.arange(4).reshape(2, 2) # 按行合并 c = np.append(a, b, axis=0) print('按行合并后的结果') print(c) print('合并后数据维度', c.shape) # 按列合并 d = np.append(a, b, axis=1) print('按列合并后的结果') print(d) print('合并后数据维度', d.shape) |
输出结果:
按行合并后的结果
[[0 1]
[2 3]
[0 1]
[2 3]]
合并后数据维度 (4, 2)
按列合并后的结果
[[0 1 0 1]
[2 3 2 3]]
合并后数据维度 (2, 4)
(2)concatenate
沿指定轴连接数组或矩阵
|
1 2 3 4 5 6 7 8 |
import numpy as np a =np.array([[1, 2], [3, 4]]) b = np.array([[5, 6]]) c = np.concatenate((a, b), axis=0) print(c) d = np.concatenate((a, b.T), axis=1) print(d) |
输出结果:
[[1 2]
[3 4]
[5 6]]
[[1 2 5]
[3 4 6]]
(3)stack
沿指定轴堆叠数组或矩阵
|
1 2 3 4 5 |
import numpy as np a =np.array([[1, 2], [3, 4]]) b = np.array([[5, 6], [7, 8]]) print(np.stack((a, b), axis=0)) |
输出结果:
[[[1 2]
[3 4]]
[[5 6]
[7 8]]]
1.5 批量处理
在深度学习中,由于源数据都比较大,所以通常需要采用批处理。如利用批量来计算梯度的随机梯度法(SGD),就是一个典型应用。深度学习的计算一般比较复杂,加上数据量一般比较大,如果一次处理整个数据,往往出现资源瓶颈。为了更有效的计算,一般将整个数据集分成小批量。与处理整个数据集的另一个极端是每次处理一条记录,这种方法也不科学,一次处理一条记录无法充分发挥GPU、NumPy平行处理优势。因此,实际使用中往往采用批量处理(mini-batch)。
如何把大数据拆分成多个批次呢?可采用如下步骤:
(1)得到数据集
(2)随机打乱数据
(3)定义批大小
(4)批处理数据集
以下我们通过一个示例来具体说明:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np #生成10000个形状为2X3的矩阵 data_train = np.random.randn(10000,2,3) #这是一个3维矩阵,第一个维度为样本数,后两个是数据形状 print(data_train.shape) #(10000,2,3) #打乱这10000条数据 np.random.shuffle(data_train) #定义批量大小 batch_size=100 #进行批处理 for i in range(0,len(data_train),batch_size): x_batch_sum=np.sum(data_train[i:i+batch_size]) print("第{}批次,该批次的数据之和:{}".format(i,x_batch_sum)) |
最后5行结果:
第9500批次,该批次的数据之和:17.63702580438092
第9600批次,该批次的数据之和:-1.360924607368387
第9700批次,该批次的数据之和:-25.912226239266445
第9800批次,该批次的数据之和:32.018136957835814
第9900批次,该批次的数据之和:2.9002576614446935
【说明】
批次从0开始,所以最后一个批次是9900。
1.6 通用函数
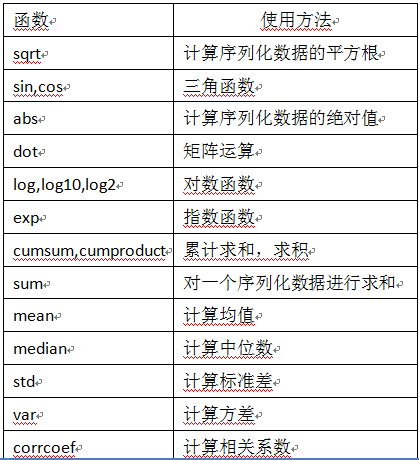
NumPy提供了两种基本的对象,即ndarray和ufunc对象。前面我们介绍了ndarray,本节将介绍NumPy的另一个对象通用函数(ufunc),ufunc是universal function的缩写,它是一种能对数组的每个元素进行操作的函数。许多ufunc函数都是用c语言级别实现的,因此它们的计算速度非常快。此外,它们比math模块中函数更灵活。math模块的输入一般是标量,但NumPy中函数可以是向量或矩阵,而利用向量或矩阵可以避免使用循环语句,这点在机器学习、深度学习中非常重要。表1-5为NumPy常用的几个通用函数。
表1-5 NumPy几个常用通用函数
(1)math与numpy函数的性能比较:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import time import math import numpy as np x = [i * 0.001 for i in np.arange(1000000)] start = time.clock() for i, t in enumerate(x): x[i] = math.sin(t) print ("math.sin:", time.clock() - start ) x = [i * 0.001 for i in np.arange(1000000)] x = np.array(x) start = time.clock() np.sin(x) print ("numpy.sin:", time.clock() - start ) |
打印结果
math.sin: 0.5169950000000005
numpy.sin: 0.05381199999999886
由此可见,numpy.sin比math.sin快近10倍。
(2)循环与向量运算比较:
充分使用Python的NumPy库中的内建函数(built-in function),实现计算的向量化,可大大提高运行速度。NumPy库中的内建函数使用了SIMD指令。如下使用的向量化要比使用循环计算速度快得多。如果使用GPU,其性能将更强大,不过NumPy不支持GPU。Pytorch支持GPU,第5章将介绍Pytorch如何使用GPU来加速算法。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import time import numpy as np x1 = np.random.rand(1000000) x2 = np.random.rand(1000000) ##使用循环计算向量点积 tic = time.process_time() dot = 0 for i in range(len(x1)): dot+= x1[i]*x2[i] toc = time.process_time() print ("dot = " + str(dot) + "\n for loop----- Computation time = " + str(1000*(toc - tic)) + "ms") ##使用numpy函数求点积 tic = time.process_time() dot = 0 dot = np.dot(x1,x2) toc = time.process_time() print ("dot = " + str(dot) + "\n verctor version---- Computation time = " + str(1000*(toc - tic)) + "ms") |
输出结果
dot = 250215.601995
for loop----- Computation time = 798.3389819999998ms
dot = 250215.601995
verctor version---- Computation time = 1.885051999999554ms
从运行结果上来看,使用for循环的运行时间大约是向量运算的400倍。因此,深度学习算法中,一般都使用向量化矩阵运算。
1.7 广播机制
NumPy的Universal functions 中要求输入的数组shape是一致的,当数组的shape不相等的时候,则会使用广播机制。不过,调整数组使得shape一样,需满足一定规则,否则将出错。这些规则可归结为以下四条:
(1)让所有输入数组都向其中shape最长的数组看齐,shape中不足的部分都通过在前面加1补齐;
如:a:2x3x2 b:3x2,则b向a看齐,在b的前面加1:变为:1x3x2
(2)输出数组的shape是输入数组shape的各个轴上的最大值;
(3)如果输入数组的某个轴和输出数组的对应轴的长度相同或者其长度为1时,这个数组能够用来计算,否则出错;
(4)当输入数组的某个轴的长度为1时,沿着此轴运算时都用(或复制)此轴上的第一组值。
广播在整个NumPy中用于决定如何处理形状迥异的数组;涉及算术运算包括(+,-,*,/…)。这些规则说的很严谨,但不直观,下面我们结合图形与代码进一步说明:
目的:A+B
其中A为4x1矩阵,B为一维向量 (3,)
要相加,需要做如下处理:
(1)根据规则1,B需要向看齐,把B变为(1,3)
(2)根据规则2,输出的结果为各个轴上的最大值,即输出结果应该为(4,3)矩阵
那么A如何由(4,1)变为(4,3)矩阵?B如何由(1,3)变为(4,3)矩阵?
3)根据规则4,用此轴上的第一组值(要主要区分是哪个轴),进行复制(但在实际处理中不是真正复制,否则太耗内存,而是采用其它对象如ogrid对象,进行网格处理)即可,
详细处理如图1-4所示。
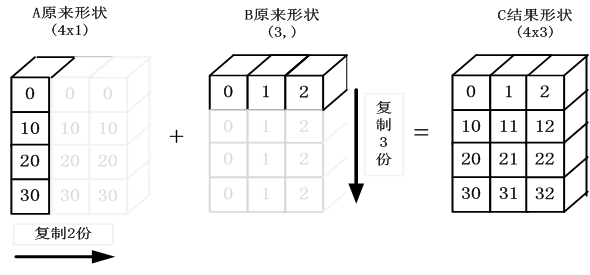
图1-4 NumPy广播规则示意图
代码实现
|
1 2 3 4 5 6 7 |
import numpy as np A = np.arange(0, 40,10).reshape(4, 1) B = np.arange(0, 3) print("A矩阵的形状:{},B矩阵的形状:{}".format(A.shape,B.shape)) C=A+B print("C矩阵的形状:{}".format(C.shape)) print(C) |
运行结果
A矩阵的形状:(4, 1),B矩阵的形状:(3,)
C矩阵的形状:(4, 3)
[[ 0 1 2]
[10 11 12]
[20 21 22]
[30 31 32]]
1.8 小结
本章主要介绍了NumPy模块的常用操作,尤其涉及对矩阵的操作,这些操作在后续程序中经常使用。NumPy内容很丰富,这里只列了一些主要内容,如果你想了解更多内容,可登录NumPy官网:http://www.numpy.org/
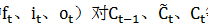 等信息进行过滤。
等信息进行过滤。