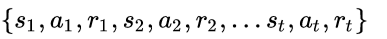第22章 强化学习基础
22.1强化学习简介
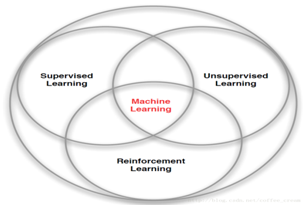
强化学习是机器学习中的一种算法, 如下图，它是让计算机实现从一开始什么都不懂, 不像监督学习或无监督学习有大量的经验或输入数据, 它基本算自学成才。通过不断地尝试, 从错误或惩罚中学习, 最后找到规律, 学会了达到目的的方法. 这就是一个完整的强化学习过程。
强化学习已经在如游戏，机器人等领域中开花结果。各大科技公司，如中国的百度、阿里美国的谷歌、facebook、微软等更是将强化学习技术作为其重点发展的技术之一。可以说强化学习算法正在改变和影响着这个世界，掌握了这门技术就掌握了改变世界和影响世界的工具。
强化学习应用非常广泛，目前主要领域有：
游戏理论与多主体交互
机器人
电脑网络
车载导航
医学
工业物流
强化学习的原理大致如下图：
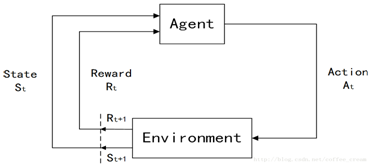
其中：
主体（agent）
是动作的行使者，例如配送货物的无人机，或者电子游戏中奔跑跳跃的超级马里奥。
状态（state）
是主体的处境，亦即一个特定的时间和地点、一项明确主体与工具、障碍、敌人或奖 品等其他重要事物的关系的配置。
动作（action）
其含义不难领会，但应当注意的是，主体需要在一系列潜在动作中进行选择。在电子 游戏中，这一系列动作可包括向左或向右跑、不同高度的跳跃、蹲下和站着不动。在 股票市场中，这一系列动作可包括购买、出售或持有一组证券及其衍生品中的任意一 种。无人飞行器的动作选项则包括三维空间中的许多不同的速度和加速度等。
奖励（reward）
是用于衡量主体的动作成功与否的反馈。例如，在电子游戏中，如果马里奥接触一枚 金币，他就能赢得分数。主体向环境发出以动作为形式的输出，而环境则返回主体的 新状态及奖励。
环境(environment)
其主体被“嵌入”并能够感知和行动的外部系统。
输入是：
State
为 Observation，例如迷宫的每一格是一个State
Actions
在每个状态下，有什么行动
Reward
进入每个状态时，能带来正面或负面的回报
输出就是：
Policy
在每个状态下，会选择哪个行动
具体来说就是：
State = 迷宫中Agent的位置，可以用一对座标表示，例如(1,3)
Action = 在迷宫中每一格，你可以行走的方向，例如：｛上，下，左，右｝
Reward = 当前的状态 (current state) 之下，迷宫中的一格可能有食物 (+1) ,也可能有怪兽 (-100)
Policy = 一个由状态 → 行动的函数，即： 函数对给定的每一个状态，都会给出一个行动。
增强学习的任务就是找到一个最优的策略Policy从而使Reward最多。
我们一开始并不知道最优的策略是什么，因此往往从随机的策略开始，使用随机的策略进行试验，就可以得到一系列的状态,动作和反馈：
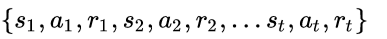
这就是一系列的样本Sample。增强学习的算法就是需要根据这些样本来改进Policy，从而使得得到的样本中的Reward更好。
22.2强化学习常用算法
强化学习有多种算法,目前比较常用的算法, 有通过行为的价值来选取特定行为的方法, 如 Q-learning, Sarsa, 使用神经网络学习的 DQN(Deep Q Network), 以及DQN的后续算法，还有直接输出行为的 policy gradients等。限于篇幅，这里我们主要介绍几种具有代表性算法。
22.2.1 Q-Learning算法
利用 Q-Learning 训练计算机玩 Atari 游戏的时候，Q-Learning 曾引起了轰动。现在，Q-Learning 依然是一个有重大意义的概念。大多数现代的强化学习算法，都是 Q-Learning 的一些改进。
（1）其主流程大致如下：
（2）Q-learning的伪代码为：
初始化价值表Q(s,a)
观察当前状态 s
根据策略(比如贪心算法)选择一个动作a
执行这个动作，观察奖励r和新状态s
使用观察到的奖励和下一个状态可能的最大奖励来更新状态的价值。更新是基于下述公式和参数。
将状态设置为新状态，并重复该过程，直到达到终端状态。
（3）在Q-Learning中，函数Q(s,a)是代表机器人在状态s时采取动作a所得到的未来价值回报，可能有读者就有疑问了，当前我采取了动作a，我怎么知道我当前这个做法在未来的价值回报是多少？确实不能，如果我们仅仅知道当下的状态、动作，而不知道紧接下来的动作及其回报。
怎么求Q(s,a)是一个摆在我们面前的大问题，虽然我们无法确切的知道Q(s,a)是多少，但是我们可以在心里面假想这个Q(s,a)一定是存在的，一旦Q(s,a)存在，于是我们在每一个状态s时，只需采取满足Q(s,a)最大的那个动作a了。
如何计算Q(s,a)？我们可以回顾一下Bellman方程，即前后两个相邻的Q(s,a)必须满足的关系，简单说就是当前采取的行动的最大价值回报等于瞬时回报加上下一个状态的最大回报。顺此思路，Q-Learning的做法就是使用此Bellman方程不断逼近Q(s,a)。
Q-Learning最简单最直接的做法就是构建一个状态-动作表，该表中存储着每个状态采取每个动作时候的Q值。该做法的流程可以总结如下：
假设状态数目为A，动作数目为B
• 随机初始化数组Q[A, B]
• 定义或获取初始状态s
• 重复以下步骤直到数组Q收敛
(1) 选取一个动作a并且执行
(2) 接受回报R，同时转移到下一个状态s’
(3) 更新Q[s , a]的值
(4) 状态变为s’，并返回到步骤(1)
可以看到，使用Q[s,a]来进行Q-Learning的算法流程非常简单，不过上述算法中有以下几个值得思考的关键点：
第一，如何选取动作a？
如果仅仅是采取贪婪的算法，在每个状态s处挑选让此状态达到最大值的动作a，这种做法眼光太狭隘，只注重眼前利益，不顾长远回报，其使得expoitation达到了最大，exploration却最小，最终陷入局部最优。因此比较好的办法是在选取动作a的时候，既要注重expoitation，又要考虑exploration，可以采取e-greedy算法，设定一定的概率让机器人随机采取动作，其余时候贪婪做出决策。
第二，如何更新Q[s,a]的值？
前面说了，由Bellman方程可知，Q[s,a]=R+max(Q[s',:])，从梯度下降的角度看，这个新的Q[s,a]是在s状态下求出的最大未来回报，也是我们渴望逼近的值，但是我们在更新旧的Q[s,a]的时候，不能将此新的Q[s,a]直接替代旧的Q[s,a]，因为这个新的Q[s,a]只是我们的一种估计，甚至是一种带噪声的估计。因此，不能直接使用新的Q[s,a]去取代旧的Q[s,a]，而应该是让旧的Q[s,a]朝着新的Q[s,a]走一小步，用公式描述就是：
Q[s,a]=Q[s,a]+lr*(R+gamma*max(Q[s',:])-Q[s,a])
其中lr是学习率，gamma是折扣因子，之所以使用折扣因子是因为，环境可能是随机的，我们无法完全确保在下一次采取同样的动作还是会得到同样的回报值。折扣因子一般介于0和1之间。
第三，除了使用e-greedy算法选取动作，是否还可以使用其他技巧？
答案是可以的，比如，在每一个状态s时，当我们计算Q[s,:]的最大值时可以先随机添加一点高斯噪声到Q[s,:]上再求最大值，这样也可以起到了exploration的作用，这种方法的好处就是我们在鼓励exploration的同时也照顾了Q值，而不是纯粹的随机选取。我想，在训练的不同阶段，我们可以组合这两种技巧，比如在训练开始的时候，采取e-greedy算法，而一定周期以后，就采取添加噪声的算法。
Q-Learning算法是一种离策略算法(off-policy)，即其Q函数更新不同于选取动作时遵循的策略，换句话说，Q函数更新时计算了下一个状态的最大价值，但是取那个最大值的时候的行动与当前策略是无关的。后面我们将介绍一种on-policy策略算法，即sarsa算法。
正如我之前所说，Q-Learning是一种off-policy的强化学习算法，即其Q表的更新不同于选取动作时所遵循的策略，换句化说，Q表在更新的时候计算了下一个状态的最大价值，但是取那个最大值的时候所对应的行动不依赖于当前策略。
用公式来表示Q-Learning中Q表的更新：
Q(St,At) = Q(St,At) + lr [R(t+1) + discount * max Q(St+1,a) – Q(St,At)]
根据以上公式，我们就可以写Q-Learning算法描述如下：
其代码如何实现？后面我们将结合具体实例来说明其详细代码实现。
22.2.2 Sarsa算法
Sarsa算法与Q-learning算法非常相似，所不同的就是更新Q值时，Sarca的现实值取R+γQ(S',A')，而不是R+γmax_a'Q(S',a')，而Q learning是使用R+γmax_a'Q(S',a')。
其算法逻辑为：
22.2.3 DQN算法
DQN(Deep Q Network) 由 DeepMind 在 2013 年在 NIPS 提出。它融合了神经网络和 Q learning 的方法。DQN 算法的主要做法是 Experience Replay，其将系统探索环境得到的数据储存起来，然后随机采样样本更新深度神经网络的参数。
Experience Replay 的动机是：
1）深度神经网络作为有监督学习模型，要求数据满足独立同分布。
2）但 Q Learning 算法得到的样本前后是有关系的。为了打破数据之间的关联性，Experience Replay 方法通过存储-采样的方法将这个关联性打破了。
DeepMind 在 2015 年初在 Nature 上发布了文章，引入了 Target Q 的概念，进一步打破数据关联性。Target Q 的概念是用旧的深度神经网络 w− 去得到目标值，下面是带有 Target Q 的 Q Learning 的优化目标。
J=min(r+γmaxa′Q(s′,a′,w−))−Q(s,a,w))2
Q-learning最早是根据一张Q-table，即各个状态动作的价值表来完成的，通过动作完成后的奖励不断迭代更新这张表，来完成学习过程。然而当状态过多或者离散时，这种方法自然会造成维度灾难，所以我们才要用一个神经网络来表达出这张表，也就是Q-Network。
如下图，把Q-table换为神经网络，利用神经网络参数替代Q-table。
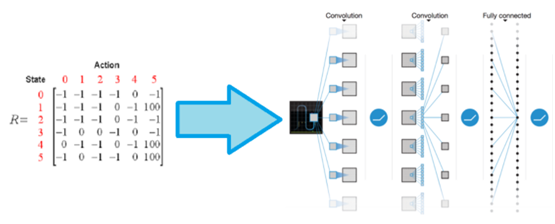
通过前面两个卷积层，我们完全不需要费心去理解环境中的状态和动作奖励，只需要将状态参数一股脑输入就好。当然，我们的数据特征比较简单，无需进行池化处理，所以后面两层直接使用全连接即可。
主体算法如下：
22.3强化学习实例
22.3.1强化学习寻宝实例
这节我们用 tabular Q-learning 的方法实现一个小例子, 例子的环境是一个一维世界或一条线段上, 在世界的右边有宝藏, 探索者只要得到宝藏就将获得奖励, 然后以后就记住了得到宝藏的方法。其环境图像如下：
|
|
-o---T # T 就是宝藏的位置, o 是探索者的位置 |
Q-learning 是一种记录行为值 (Q value) 的方法, 每种在一定状态的行为都会有一个值 Q(s, a), 就是说 行为 a 在 s 状态的值是 Q(s, a). s 在上面的探索者游戏中, 就是 o 所在的地点了. 而每一个地点探索者都能做出两个行为 left/right, 这就是探索者的所有可行的 a。
如果在某个地点 s1, 探索者计算了他能有的两个行为, a1/a2=left/right, 计算结果是 Q(s1, a1) > Q(s1, a2), 那么探索者就会选择 left 这个行为. 这就是 Q learning 的行为选择简单规则。
22.3.1.1算法的详细过程
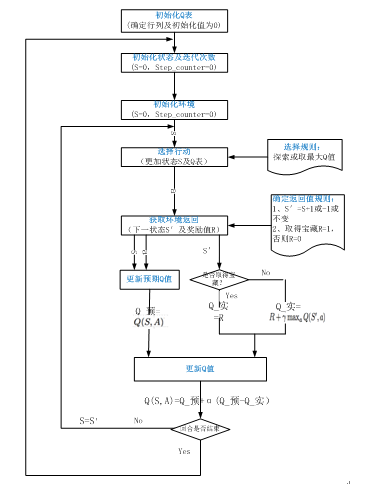
22.3.1.2代码实现
这里我使用python3.6
1）导入必要的库
|
|
import numpy as np import pandas as pd import time N_STATES = 8 # 1维世界的宽度 ACTIONS = ['left', 'right'] # 探索者的可用动作 EPSILON = 0.9 # 贪婪度 greedy ALPHA = 0.1 # 学习率 GAMMA = 0.9 # 奖励递减值 MAX_EPISODES = 20 # 最大回合数 |
2）创建Q表
对于 tabular Q learning, 我们必须将所有的 Q values (行为值) 放在 q_table 中, 更新 q_table 也是在更新他的行为准则. q_table 的 index 是所有对应的 state (探索者位置), columns 是对应的 action (探索者行为).
|
|
def build_q_table(n_states, actions): table = pd.DataFrame( np.zeros((n_states, len(actions))), # q_table 全 0 初始 columns=actions, # columns 对应的是行为名称 ) return table |
格式如下：
# q_table:
"""
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.0
5 0.0 0.0
"""
3）定义动作
接着定义探索者是如何挑选行为的. 这是我们引入 epsilon greedy 的概念. 因为在初始阶段, 随机的探索环境, 往往比固定的行为模式要好, 所以这也是累积经验的阶段, 我们希望探索者不会那么贪婪(greedy). 所以 EPSILON 就是用来控制贪婪程度的值. EPSILON 可以随着探索时间不断提升(越来越贪婪), 不过在这个例子中, 我们就固定成 EPSILON = 0.9, 90% 的时间是选择最优策略, 10% 的时间来探索.
|
|
# 在某个 state 地点, 选择行为 def choose_action(state, q_table): state_actions = q_table.iloc[state, :] # 选出这个 state 的所有 action 值 if (np.random.uniform() > EPSILON) or (state_actions.all() == 0): # 非贪婪 or 或者这个 state 还没有探索过 action_name = np.random.choice(ACTIONS) else: action_name = state_actions.argmax() # 贪婪模式 return action_name |
4）获取环境反馈信息
做出行为后, 环境也要给我们的行为一个反馈, 反馈出下个 state (S_) 和 在上个 state (S) 做出 action (A) 所得到的 reward (R). 这里定义的规则就是, 只有当 o 移动到了 T, 探索者才会得到唯一的一个奖励, 奖励值 R=1, 其他情况都没有奖励。
|
|
def get_env_feedback(S, A): # This is how agent will interact with the environment if A == 'right': # move right if S == N_STATES - 2: # terminate S_ = 'terminal' R = 1 else: S_ = S + 1 R = 0 else: # move left R = 0 if S == 0: S_ = S # reach the wall else: S_ = S - 1 return S_, R |
5）更新环境
|
|
def update_env(S, episode, step_counter): # This is how environment be updated env_list = ['-']*(N_STATES-1)+['T'] # '---------T' our environment if S == 'terminal': interaction = 'Episode %s: total_steps = %s' % (episode+1, step_counter) print('\r{}'.format(interaction), end='\n') time.sleep(2) print('\r ', end='') else: env_list[S] = 'o' interaction = ''.join(env_list) print('\r{}'.format(interaction), end='') time.sleep(FRESH_TIME) |
6）强化学习主循环
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
def rl(): q_table = build_q_table(N_STATES, ACTIONS) # 初始 q table for episode in range(MAX_EPISODES): # 回合 step_counter = 0 S = 0 # 回合初始位置 is_terminated = False # 是否回合结束 update_env(S, episode, step_counter) # 环境更新 while not is_terminated: A = choose_action(S, q_table) # 选行为 S_, R = get_env_feedback(S, A) # 实施行为并得到环境的反馈 q_predict = q_table.loc[S, A] # 估算的(状态-行为)值 if S_ != 'terminal': q_target = R + GAMMA * q_table.iloc[S_, :].max() # 实际的(状态-行为)值 (回合没结束) else: q_target = R # 实际的(状态-行为)值 (回合结束) is_terminated = True # terminate this episode q_table.loc[S, A] += ALPHA * (q_target - q_predict) # q_table 更新 S = S_ # 探索者移动到下一个 state update_env(S, episode, step_counter+1) # 环境更新 step_counter += 1 return q_table |
7）运行主程序
|
|
if __name__ == "__main__": q_table = rl() print('\r\nQ-table:\n') print(q_table) |
运行结果：
Episode 1: total_steps = 46
Episode 2: total_steps = 66
Episode 3: total_steps = 52
Episode 4: total_steps = 21
Episode 5: total_steps = 31
Episode 6: total_steps = 12
Episode 7: total_steps = 10
Episode 8: total_steps = 7
Episode 9: total_steps = 7
Episode 10: total_steps = 7
Episode 11: total_steps = 7
Episode 12: total_steps = 7
Episode 13: total_steps = 7
Episode 14: total_steps = 7
Episode 15: total_steps = 7
Q-table:
left right
0 1.324169e-07 0.000238
1 1.479568e-07 0.001645
2 6.925792e-07 0.009356
3 5.968673e-06 0.042724
4 6.631859e-05 0.152157
5 1.385100e-04 0.407920
6 8.100000e-04 0.794109
7 0.000000e+00 0.000000
从以上结果可以看出，为找到宝藏，前几次查询步骤比较多，但后来，她就越来越聪明了，后来从开始位置，只要7步了，可以说直奔宝藏了。
22.3.2强化学习立杆实例
这里我们用一个走迷宫例子来实现 RL方法，即Sarsa(state-action-reward-state_-action_). 我们从这一个简称可以了解到, Sarsa 的整个循环都将是在一个路径上, 也就是 on-policy, 下一个 state_, 和下一个 action_ 将会变成他真正采取的 action 和 state. 和 Qlearning 的不同之处就在这. Qlearning 的下个一个 state_ action_ 在算法更新的时候都还是不确定的 (off-policy). 而 Sarsa 的 state_, action_ 在这次算法更新的时候已经确定好了 (on-policy)。
整个算法还是一直不断更新 Q table 里的值, 然后再根据新的值来判断要在某个 state 采取怎样的 action. 不过与 Qlearning 不同之处:
1）Sarsa在当前 state 已经想好了 state 对应的 action, 而且想好了 下一个 state_ 和下一个 action_ ，但Qlearning 还没有想好下一个 action_。
2）Sarsa更新 Q(s,a) 的时候基于的是下一个 Q(s_, a_) ,而Qlearning 是基于 maxQ(s_)。
22.3.2.1算法的代码实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
from maze_env import Maze from RL_brain import SarsaTable def update(): for episode in range(100): # initial observation observation = env.reset() # RL choose action based on observation action = RL.choose_action(str(observation)) while True: # fresh env env.render() # RL take action and get next observation and reward observation_, reward, done = env.step(action) # RL choose action based on next observation action_ = RL.choose_action(str(observation_)) # RL learn from this transition (s, a, r, s, a) ==> Sarsa RL.learn(str(observation), action, reward, str(observation_), action_) # swap observation and action observation = observation_ action = action_ # break while loop when end of this episode if done: break # end of game print('game over') env.destroy() if __name__ == "__main__": env = Maze() RL = SarsaTable(actions=list(range(env.n_actions))) env.after(100, update) env.mainloop() |
【说明】
环境设计程序maze_env.py, 算法实现程序RL_brain.py，大家可以访问获取：
https://github.com/MorvanZhou/Reinforcement-learning-with-tensorflow/tree/master/contents/3_Sarsa_maze
22.3.3强化学习CartPole实例
在本次实战中，我们不选择Atari游戏，而使用OpenAI Gym中的传统增强学习任务之一CartPole作为练手的任务。游戏示意图如下：
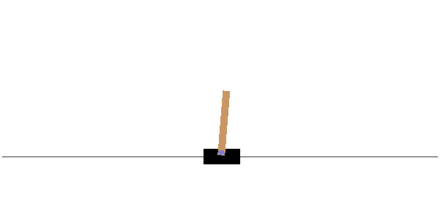
游戏的基本要求就是控制下面的cart移动，使连接在上面的杆保持垂直不倒。这个任务简化到只有两个离散动作，要么向左用力，要么向右用力。而state状态就是这个杆的位置和速度。有关这个游戏环境的详细信息可参考：https://github.com/openai/gym/wiki/CartPole-v0
下面我们就要用DQN来解决这个问题。
22.3.3.1实现这个游戏需要的基础
1）熟悉Python编程，能够使用Python基本的语法
2）对Tensorflow有一定的了解，知道基本的使用
3）知道如何使用OpenAI Gym
4）了解基本的神经网络MLP
5）理解DQN算法
22.3.3.2实现算法
我们将要实现的是最基本的DQN，也就是NIPS 13版本的DQN：
面对CartPole问题，我们进一步简化：
1）无需预处理Preprocessing。也就是直接获取观察Observation作为状态state输入。
2）只使用最基本的MLP神经网络，而不使用卷积神经网络，更不用池化层等。
22.3.3.3导入需要的库
|
|
import gym import tensorflow as tf import numpy as np import random from collections import deque |
22.3.3.4编写主循环
这里我们按照至上而下的编程方式，先写主函数用来说明整个程序架构，然后再具体编写DQN算法实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
#定义超参数 ENV_NAME = 'CartPole-v0' EPISODE = 10000 # 回合总数 STEP = 300 # 每个回合迭代次数 def main(): # 创建环境 env = gym.make(ENV_NAME) agent = DQN(env) for episode in range(EPISODE): # 初始化环境 state = env.reset() # 训练 for step in range(STEP): action = agent.egreedy_action(state) # 根据状态，随机获取行动 #接下来我们将使用env.step()执行随机的Action,并获取返回值 #如果done标记为True,则表示这次试验结束，即倾角超过15度 #或者偏离中心过远导致任务失败 next_state,reward,done,_ = env.step(action) # 反馈奖励值，done表示训练失败 reward_agent = -1 if done else 0.1 #存储信息 agent.perceive(state,action,reward,next_state,done) state = next_state if done: break if __name__ == '__main__': main() |
22.3.3.5相关函数
接下来我们编写一个DQN的函数，DQN的一切都将封装在里面。在主函数中，我们只需调用
|
|
agent.egreedy_action(state) # 获取包含随机的动作 agent.perceive(state,action,reward,next_state,done) # 感知信息 |
egreedy_action输入状态，输出动作，perceive 保存信息。
然后环境自己执行动作，输出新的状态：
|
|
next_state,reward,done,_ = env.step(action) |
然后整个过程就反复循环，一个episode结束，就执行一个。
22.3.3.6 DQN实现
1）编写基本DQN类的结构
|
|
class DQN(): # DQN Agent def __init__(self, env): #初始化 def create_Q_network(self): #创建Q网络 def create_training_method(self): #创建训练方法 def perceive(self,state,action,reward,next_state,done): #感知存储信息 def train_Q_network(self): #训练网络 def egreedy_action(self,state): #输出带随机的动作 def action(self,state): #输出动作 |
DQN一个很重要的功能就是要能存储数据，然后在训练的时候minibatch出来。所以，我们需要构造一个存储机制。这里使用deque来实现。
|
|
self.replay_buffer = deque() |
2）初始化
|
|
def __init__(self, env): # init experience replay self.replay_buffer = deque() # init some parameters self.time_step = 0 self.epsilon = INITIAL_EPSILON self.state_dim = env.observation_space.shape[0] self.action_dim = env.action_space.n self.create_Q_network() self.create_training_method() # Init session self.session = tf.InteractiveSession() self.session.run(tf.global_variables_initializer()) |
这里要注意一点就是egreedy的epsilon是不断变小的，也就是随机性不断变小。怎么理解呢？就是一开始需要更多的探索，所以动作偏随机，慢慢的我们需要动作能够有效，因此减少随机。
3）创建Q网络
我们这里创建最基本的MLP，输入层为state_dim(其值为4）个节点、隐含层节点数设置为20，输出层节点数为action_dim(其值为2)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def create_Q_network(self): # network weights W1 = self.weight_variable([self.state_dim,20]) b1 = self.bias_variable([20]) W2 = self.weight_variable([20,self.action_dim]) b2 = self.bias_variable([self.action_dim]) # input layer self.state_input = tf.placeholder("float",[None,self.state_dim]) # hidden layers h_layer = tf.nn.relu(tf.matmul(self.state_input,W1) + b1) # Q Value layer self.Q_value = tf.matmul(h_layer,W2) + b2 def weight_variable(self,shape): initial = tf.truncated_normal(shape) return tf.Variable(initial) def bias_variable(self,shape): initial = tf.constant(0.01, shape = shape) return tf.Variable(initial) |
这里我们只用了一个隐层，然后使用relu非线性单元。另外，需注意state 输入的格式，因为使用minibatch，所以格式是[None,state_dim]
4）写perceive函数
|
|
def perceive(self,state,action,reward,next_state,done): one_hot_action = np.zeros(self.action_dim) one_hot_action[action] = 1 self.replay_buffer.append((state,one_hot_action,reward,next_state,done)) if len(self.replay_buffer) > REPLAY_SIZE: self.replay_buffer.popleft() if len(self.replay_buffer) > BATCH_SIZE: self.train_Q_network() |
这里action值与动作的对应关系为：0表示把cart往左推；1表示把cart往右推、为便于计算起见，对表示动作数据格式做了转换。使用了在神经网络中one hot key的形式，而在OpenAI Gym中则使用单值。什么意思呢？比如我们输出动作是1，那么对应的one hot形式就是[0,1]，如果输出动作是0，那么one hot 形式就是[1,0]。这样做的目的是为了之后更好的进行计算。
在perceive中一个最主要的事情就是存储。然后根据情况进行train。这里我们要求只要存储的数据大于Batch的大小就开始训练。
5）编写action输出函数
|
|
def egreedy_action(self,state): Q_value = self.Q_value.eval(feed_dict = {self.state_input:[state]})[0] if random.random() <= self.epsilon: return random.randint(0,self.action_dim - 1) else: return np.argmax(Q_value) self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON)/10000 def action(self,state): return np.argmax(self.Q_value.eval(feed_dict = {self.state_input:[state]})[0]) |
输出有两种可能，一个是根据情况输出随机动作，一个是根据神经网络输出。由于神经网络输出的是每一个动作的Q值，因此我们选择最大的那个Q值对应的动作输出。
6）编写training method函数
|
|
def create_training_method(self): self.action_input = tf.placeholder("float",[None,self.action_dim]) # one hot presentation self.y_input = tf.placeholder("float",[None]) Q_action = tf.reduce_sum(tf.multiply(self.Q_value,self.action_input),reduction_indices = 1) self.cost = tf.reduce_mean(tf.square(self.y_input - Q_action)) self.optimizer = tf.train.AdamOptimizer(0.0001).minimize(self.cost) |
这里的y_input就是target Q值。我们这里采用Adam优化器，其实随便选择一个必然SGD，RMSProp都是可以的。可能比较不好理解的就是Q值的计算。这里大家记住动作输入是one hot key的形式，因此将Q_value和action_input向量相乘得到的就是这个动作对应的Q_value。然后用reduce_sum将数据维度压成一维。
7）编写training函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
def train_Q_network(self): self.time_step += 1 # Step 1: obtain random minibatch from replay memory minibatch = random.sample(self.replay_buffer,BATCH_SIZE) state_batch = [data[0] for data in minibatch] action_batch = [data[1] for data in minibatch] reward_batch = [data[2] for data in minibatch] next_state_batch = [data[3] for data in minibatch] # Step 2: calculate y y_batch = [] Q_value_batch = self.Q_value.eval(feed_dict={self.state_input:next_state_batch}) for i in range(0,BATCH_SIZE): done = minibatch[i][4] if done: y_batch.append(reward_batch[i]) else : y_batch.append(reward_batch[i] + GAMMA * np.max(Q_value_batch[i])) self.optimizer.run(feed_dict={ self.y_input:y_batch, self.action_input:action_batch, self.state_input:state_batch }) |
先进行minibatch工作，然后根据batch计算y_batch。最后用optimizer进行优化。
8）测试模型代码
|
|
# Test every 100 episodes if episode % 100 == 0: total_reward = 0 for i in range(TEST): state = env.reset() for j in range(STEP): env.render() action = agent.action(state) # direct action for test state,reward,done,_ = env.step(action) total_reward += reward if done: break ave_reward = total_reward/TEST print( 'episode: ',episode,'Evaluation Average Reward:',ave_reward) if ave_reward >= 200: break |
测试中唯一的不同就是我们使用
|
|
action = agent.action(state) |
来获取动作，也就是完全没有随机性，只根据神经网络来输出，没有探索，同时这里也就不再perceive输入信息来训练。
22.3.3.7 完整代码
修改了部分代码，主要是为适应新版本的要求。以下代码我的运行环境为：python3.6,tensorflow1.3,在ipython中运行。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 |
import gym import tensorflow as tf import numpy as np import random from collections import deque # Hyper Parameters for DQN GAMMA = 0.9 # discount factor for target Q INITIAL_EPSILON = 0.5 # starting value of epsilon FINAL_EPSILON = 0.01 # final value of epsilon REPLAY_SIZE = 1000 # experience replay buffer size BATCH_SIZE = 32 # size of minibatch tf.reset_default_graph() class DQN(): # DQN Agent def __init__(self, env): # init experience replay self.replay_buffer = deque() # init some parameters self.time_step = 0 self.epsilon = INITIAL_EPSILON self.state_dim = env.observation_space.shape[0] self.action_dim = env.action_space.n self.create_Q_network() self.create_training_method() # Init session self.session = tf.InteractiveSession() self.session.run(tf.global_variables_initializer()) def create_Q_network(self): # network weights W1 = tf.get_variable(name='w1',shape=[self.state_dim,20],initializer=tf.random_normal_initializer(mean=0, stddev=1)) b1 = tf.get_variable(name='b1',shape=[20]) W2 = tf.get_variable(name='w2',shape=[20,self.action_dim],initializer=tf.random_normal_initializer(mean=0, stddev=1)) b2 = tf.get_variable(name='b2',shape=[self.action_dim]) # input layer self.state_input = tf.placeholder(tf.float32,[None,self.state_dim]) # hidden layers h_layer = tf.nn.relu(tf.matmul(self.state_input,W1) + b1) # Q Value layer self.Q_value = tf.matmul(h_layer,W2) + b2 def create_training_method(self): self.action_input = tf.placeholder(tf.float32,[None,self.action_dim]) # one hot presentation self.y_input = tf.placeholder(tf.float32,[None]) Q_action = tf.reduce_sum(tf.multiply(self.Q_value,self.action_input)) self.cost = tf.reduce_mean(tf.square(self.y_input - Q_action)) self.optimizer = tf.train.AdamOptimizer(0.0001).minimize(self.cost) def perceive(self,state,action,reward,next_state,done): one_hot_action = np.zeros(self.action_dim) one_hot_action[action] = 1 self.replay_buffer.append((state,one_hot_action,reward,next_state,done)) if len(self.replay_buffer) > REPLAY_SIZE: self.replay_buffer.popleft() if len(self.replay_buffer) > BATCH_SIZE: self.train_Q_network() def train_Q_network(self): self.time_step += 1 # Step 1: obtain random minibatch from replay memory minibatch = random.sample(self.replay_buffer,BATCH_SIZE) state_batch = [data[0] for data in minibatch] action_batch = [data[1] for data in minibatch] reward_batch = [data[2] for data in minibatch] next_state_batch = [data[3] for data in minibatch] # Step 2: calculate y y_batch = [] Q_value_batch = self.Q_value.eval(feed_dict={self.state_input:next_state_batch}) for i in range(0,BATCH_SIZE): done = minibatch[i][4] if done: y_batch.append(reward_batch[i]) else : y_batch.append(reward_batch[i] + GAMMA * np.max(Q_value_batch[i])) self.optimizer.run(feed_dict={ self.y_input:y_batch, self.action_input:action_batch, self.state_input:state_batch }) def egreedy_action(self,state): Q_value = self.Q_value.eval(feed_dict = { self.state_input:[state] })[0] if random.random() <= self.epsilon: return random.randint(0,self.action_dim - 1) else: return np.argmax(Q_value) self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON)/10000 def action(self,state): return np.argmax(self.Q_value.eval(feed_dict = { self.state_input:[state] })[0]) def weight_variable(self,shape): initial = tf.truncated_normal(shape) return tf.Variable(initial) def bias_variable(self,shape): initial = tf.constant(0.01, shape = shape) return tf.Variable(initial) # --------------------------------------------------------- # Hyper Parameters ENV_NAME = 'CartPole-v0' EPISODE = 1000 # Episode limitation STEP = 300 # Step limitation in an episode TEST = 10 # The number of experiment test every 100 episode def main(): # initialize OpenAI Gym env and dqn agent env = gym.make(ENV_NAME) agent = DQN(env) for episode in range(EPISODE): # initialize task state = env.reset() # Train for step in range(STEP): action = agent.egreedy_action(state) # e-greedy action for train next_state,reward,done,_ = env.step(action) # Define reward for agent reward_agent = -1 if done else 0.1 agent.perceive(state,action,reward,next_state,done) state = next_state if done: break # Test every 100 episodes if episode % 100 == 0: total_reward = 0 for i in range(TEST): state = env.reset() for j in range(STEP): env.render() action = agent.action(state) # direct action for test state,reward,done,_ = env.step(action) total_reward += reward if done: break ave_reward = total_reward/TEST print( 'episode: ',episode,'Evaluation Average Reward:',ave_reward) if ave_reward >= 200: break if __name__ == '__main__': main() |
运行结果：
episode: 0 Evaluation Average Reward: 74.7
episode: 100 Evaluation Average Reward: 95.8
episode: 200 Evaluation Average Reward: 67.0
episode: 300 Evaluation Average Reward: 14.1
episode: 400 Evaluation Average Reward: 9.8
episode: 500 Evaluation Average Reward: 9.7
episode: 600 Evaluation Average Reward: 11.3
episode: 700 Evaluation Average Reward: 11.6
episode: 800 Evaluation Average Reward: 11.3
episode: 900 Evaluation Average Reward: 12.2
参考了：
https://zhuanlan.zhihu.com/p/21477488
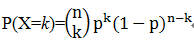
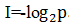。为此，可能有不少人会问，为何用对数，前面还要带上负号？
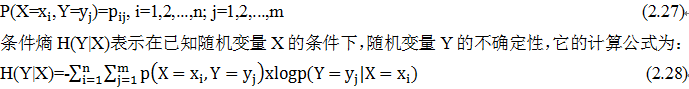
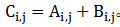。矩阵也可以和向量相加，只要它们的列数相同，相加的结果是矩阵每行与向量相加，这种隐式地复制向量b到很多位置的方式称为广播(broadcasting)，以下我们通过一个代码示例来说明。
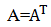成立， 则称方阵A为对称矩阵。
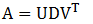(1.15)
