5.3.5 EM算法的收敛性
要证明通过迭代法求得的参数 收敛于极值点,如果能证明对应的似然函数
收敛于极值点,如果能证明对应的似然函数 收敛即可。要证明似然函数收敛,因似然函数
收敛即可。要证明似然函数收敛,因似然函数 有上界,如果能证明通过迭代,似然函数递增,则
有上界,如果能证明通过迭代,似然函数递增,则 收敛于极值点。
收敛于极值点。
假设第t次迭代时的参数为 ,通过t+1次迭代后参数为
,通过t+1次迭代后参数为 ,接下来证明
,接下来证明 。
。
由式(5.13)可得: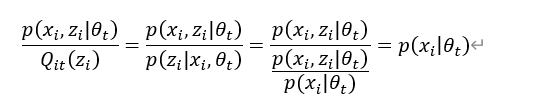
运算结果与隐变量 无关,是一个常数,根据Jensen不等式可知,式(5.12)中作为第t次迭代的结果,即把
无关,是一个常数,根据Jensen不等式可知,式(5.12)中作为第t次迭代的结果,即把 视为
视为 ,
, 改为
改为 ,则其中不等式可以取等号,即有:
,则其中不等式可以取等号,即有: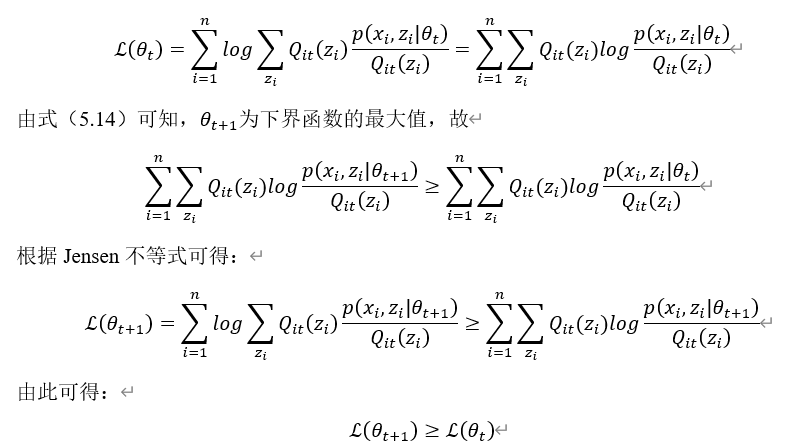
似然函数与其下界函数之间的关系,可以通过图5-10直观表示。
图5-10 EM算法中目标函数与下界函数的之间的关系
月度归档:2023年01月
5.3.4 EM算法推导
通过构建目标函数的下界函数来处理隐含变量的似然函数,该下界函数更容易优化,并通过求解下界函数的极值,构造新的下界函数,通过迭代的方法,使下界函数收敛于局部最优值。
假设概率分布 生成可观察样本为
生成可观察样本为 ,这n个样本互相独立,以及无法观察的隐含数据为
,这n个样本互相独立,以及无法观察的隐含数据为 构成完整数据,样本的模型参数为
构成完整数据,样本的模型参数为 。完整数
。完整数 的似然函数为:
的似然函数为:
下界函数通过隐变量的概率分布构造,对每个样本 ,假设
,假设 为隐变量
为隐变量 的一个概率密度函数,它们满足概率的规范性,即有:
的一个概率密度函数,它们满足概率的规范性,即有:

利用隐变量的概率分布,对原来的对数似然函数进行恒等变形。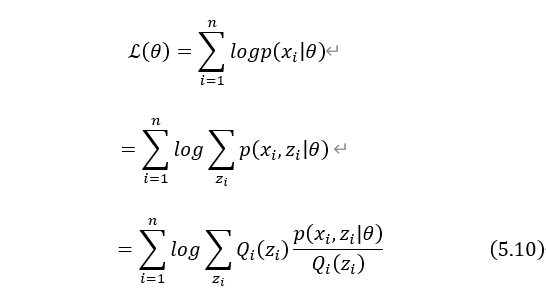
根据随机变量函数的数学期望的定义可得: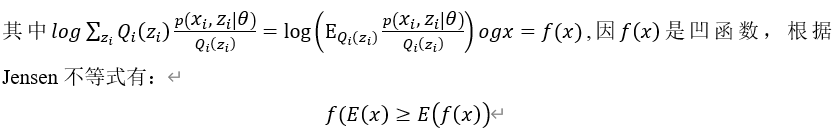
把数学期望E看成是关于 概率的期望,由式(5.10)可得:
概率的期望,由式(5.10)可得: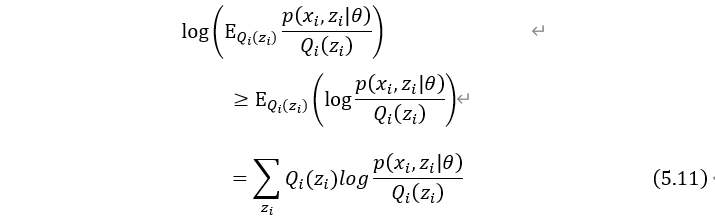
由式(5.10)、(5.11)可得: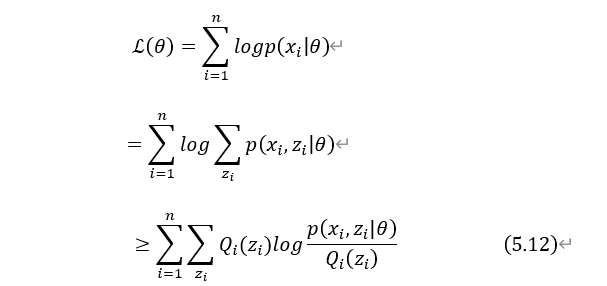
式(5.12)为似然函数 下界函数,满足条件的下界函数有很多。因为EM是迭代算法,并且是求下界函数的极值点来找到下一步迭代的参数
下界函数,满足条件的下界函数有很多。因为EM是迭代算法,并且是求下界函数的极值点来找到下一步迭代的参数 ,设
,设 为第t次迭代时参数的估计值。
为第t次迭代时参数的估计值。
如何取在 处下界函数?当然与似然函数
处下界函数?当然与似然函数 越接近越好,所以我们希望(5.12)式在
越接近越好,所以我们希望(5.12)式在 这个点能取等号。由Jensen不等式可知,等式成立的条件是随机变量是常数,故在
这个点能取等号。由Jensen不等式可知,等式成立的条件是随机变量是常数,故在 点处有:
点处有:
所以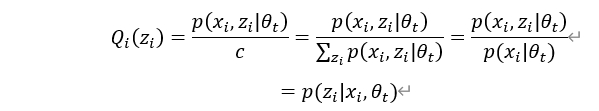
由此可知, 实际上就是隐变量
实际上就是隐变量 的后验概率
的后验概率 。
。
用 表示
表示 代入
代入  的下界函数中,得:
的下界函数中,得: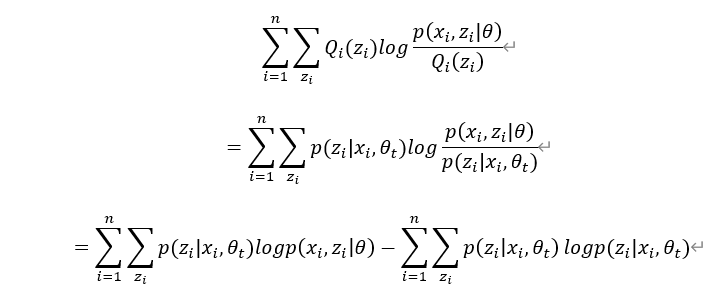
对 的下界函数中求极大值为下次迭代的参数值
的下界函数中求极大值为下次迭代的参数值 ,即有:
,即有:
到这来EM算法的推导就结束了。
下面给出EM算法的具体步骤:
(1) 初始化参数 ,然后开始循环迭代,第t次迭代的分为两步,即E步和M步。
,然后开始循环迭代,第t次迭代的分为两步,即E步和M步。
(2) E步:
基于当前参数估计值 ,构建目标函数。
,构建目标函数。
具体包括计算给定样本时对隐变量z的条件概率,即

然后计算 函数。
函数。
(3) M步
求 函数的极大值,更新参数为
函数的极大值,更新参数为 .
.

迭代第(2)和(3)步,直到参数 收敛或到指定的阈值。
收敛或到指定的阈值。
5.3.3 EM算法简单实例
根据表2的情况可知,只要知道Z,就能求出参数 。但要知道Z,又必须通过参数
。但要知道Z,又必须通过参数 推导出来,否则无法推出z的具体情况。为此,我们可以把Z看成一个隐变量,这样完整的数据就是(X,Z),通过极大似然估计对参数
推导出来,否则无法推出z的具体情况。为此,我们可以把Z看成一个隐变量,这样完整的数据就是(X,Z),通过极大似然估计对参数 进行估计,因存在隐变量z,一般无法直接用解析式表达参数,故采用迭代的方法进行优化,具体步骤如下:
进行估计,因存在隐变量z,一般无法直接用解析式表达参数,故采用迭代的方法进行优化,具体步骤如下:
输出:模型参数
EM算法具体步骤
(1)先初始化参数
(2)假设第t次循环时参数为 ,求Q函数
,求Q函数

(3)对Q函数中的参数 实现极大似然估计,得到
实现极大似然估计,得到

(4)重复第(2)和(3)步,直到收敛或指定循环步数。
其中第(2)步需要求 ,我们定义为:
,我们定义为: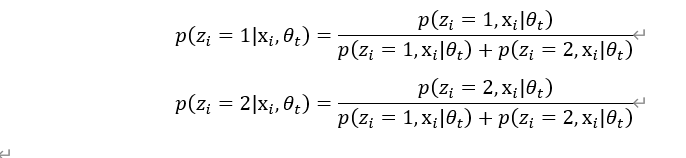
根据这个迭代步骤,第1次迭代过程如下:
(1)初始化参数
(2)E步,计算Q函数
先计算隐含变量的后验概率:

按同样方法,完成剩下4轮投掷,最后得到投掷统计信息如下表所示: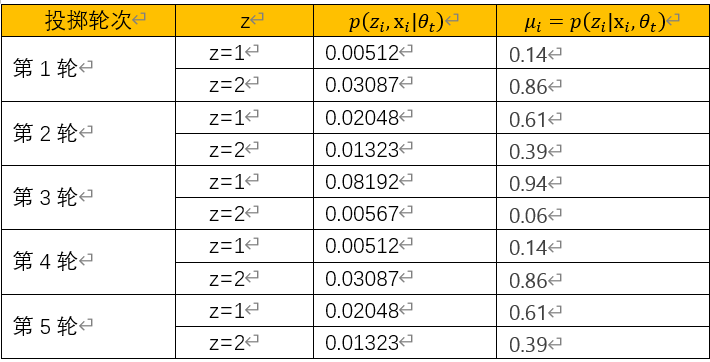
 的实现过程可用二项分布的实现,具体过程如下:
的实现过程可用二项分布的实现,具体过程如下:
计算Q函数,设 表示第i轮投掷出现正面的次数。
表示第i轮投掷出现正面的次数。
(3)对Q函数中的参数 实现极大似然估计,得到
实现极大似然估计,得到

对Q函数求导,并令导数为0。
所以
进行第2轮迭代:
基于第1轮获取的参数 ,进行第2轮EM计算:
,进行第2轮EM计算:
计算每个实验中选择的硬币是1和2的概率,计算Q函数(E步),然后在计算M步,得
继续迭代,直到收敛到指定阈值或循环次数。
以上计算过程可用Python实现
具体代入如下:
把硬币1用A表示,硬币1用B表示。H(或1)表示正面朝上,T(或0)表示反面朝上。
1、导入需要的库
|
1 2 |
import numpy as np from scipy import stats |
2、把观察数据写成矩阵
|
1 2 3 4 5 6 |
# 硬币投掷结果观测序列 observations = np.array([[1, 1, 0, 1, 0], [0, 0, 1, 1, 0], [1, 0, 0, 0, 0], [1, 0, 0, 1, 1], [0, 1, 1, 0, 0]]) |
3、单步EM算法,迭代一次算法实现步骤
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
def EM_Single(priors, observations): """ EM算法单次迭代 参数初始化 : [theta_A, theta_B] 输入样本矩阵: [m x n matrix] 返回值 -------- 新参数值: [new_theta_A, new_theta_B] """ counts = {'A': {'H': 0, 'T': 0}, 'B': {'H': 0, 'T': 0}} theta_A = priors[0] theta_B = priors[1] u_A=[] u_B=[] # E step for observation in observations: len_observation = len(observation) num_heads = observation.sum() num_tails = len_observation - num_heads # 投掷硬币A(或B)五次,这是一个二项分布问题 contribution_A = stats.binom.pmf(num_heads, len_observation, theta_A) contribution_B = stats.binom.pmf(num_heads, len_observation, theta_B) #求权重时,把二项分布中的组合数约去了 weight_A = contribution_A / (contribution_A + contribution_B) #取2位小数 weight_A=round(weight_A,2) weight_B = contribution_B / (contribution_A + contribution_B) #取2位小数 weight_B=round(weight_B,2) # 更新在当前参数下A、B硬币产生的正反面次数 counts['A']['H'] += weight_A * num_heads u_A.append(weight_A) counts['B']['H'] += weight_B * num_heads u_B.append(weight_B) # M step new_theta_A = counts['A']['H'] / (len_observation*np.sum(u_A)) new_theta_B = counts['B']['H'] / (len_observation*np.sum(u_B)) new_theta_A=round(new_theta_A,2) new_theta_B=round(new_theta_B,2) return [new_theta_A, new_theta_B] |
4、执行
|
1 |
EM_Single([0.2,0.7],observations) |
[0.35, 0.53]
与手工计算的结果一致。
5、EM算法主循环
EM算法的主循环,给定循环的两个终止条件:模型参数变化小于阈值;循环达到最大次数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
def EM(observations, prior, tol=1e-6, iterations=10): """ EM算法 :param observations: 观测数据 :param prior: 模型初值 :param tol: 迭代结束阈值 :param iterations: 最大迭代次数 :return: 局部最优的模型参数 """ iteration = 0 while iteration < iterations: new_prior = EM_Single(prior, observations) delta_change = np.abs(prior[0] - new_prior[0]) if delta_change < tol: break else: prior = new_prior iteration += 1 return [new_prior, iteration] |
6、测试
|
1 |
EM(observations, [0.20, 0.70],iterations=1) |
运行结果
[[0.35, 0.53], 1]
|
1 |
EM(observations, [0.20, 0.70],iterations=2) |
运行结果
[0.4, 0.48], 2]
|
1 |
EM(observations, [0.20, 0.70],iterations=10) |
运行结果
[[0.44, 0.44], 5]
练习
用python实现以下这个简单实例: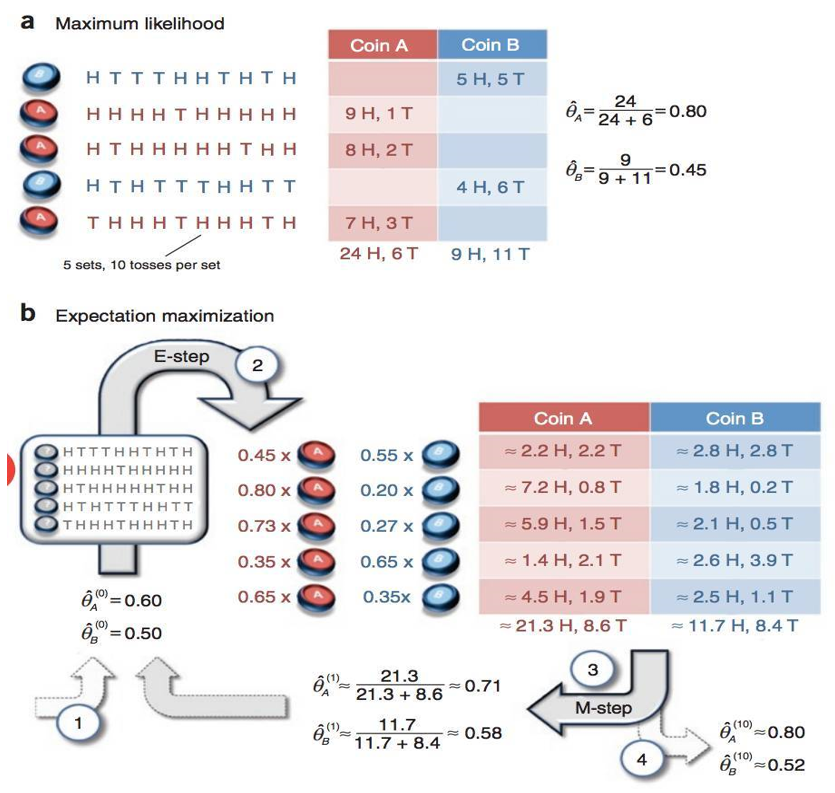
5.3EM算法
EM (expectation-maximization)算法又称期望最大化算法,是Dempster, Laind, Rubin于1977年提出的求参数极大似然估计的一种迭代优化策略, 用于含有隐变量(Hidden variable)的概率模型参数的极大似然估计(或极大后验概率估计),它可以从非完整数据集中对参数进行极大似然估计,是一种非常简单实用的学习算法。
如果模型涉及的数据都是可观察数据,可以直接使用极大似然估计或极大后验概率估计的方法求解模型参数。但当模型有隐变量时,不能简单使用极大似然估计,需要迭代的方法,迭代一般分为两步:E步,求期望;M步,求极大值。
如何更好理解EM算法?这里有几个问题,理解这些问题有助理解EM算法。
本节将回答如下几个问题:
• 何为隐变量?如何理解隐变量?采用隐变量的概率分布与全概率公式中完备概率有何区别?
• 为何使用EM算法?为何通过迭代方法能不断靠近极值点?迭代结果是递增吗?
通过简单实例说明如何使用EM算法。
• EM算法的推导过程
• 为何选择q(z│x,θ)作为逼近分布?
• EM算法是一种方法或思想,EM有哪些使用场景。
5.3.1 何为隐变量?
在统计学中,随机变量,如![x_1=[1,3,7,4],x_2=[5,2,9,8]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_dd840113e7c03d2b8b98de86afd6350b.gif) 等变量称为可观察的变量,与之相对的往往还有一些不可观测的随机变量,我们称之为隐变量或潜变量。隐变量可以通过使用数学模型依据观测得的数据被推断出来。
等变量称为可观察的变量,与之相对的往往还有一些不可观测的随机变量,我们称之为隐变量或潜变量。隐变量可以通过使用数学模型依据观测得的数据被推断出来。
为了更好说明隐变量,我们先看一个简单实例。
现在有两枚硬币1和2,假设随机抛掷后正面朝上概率分别为 。为了估计这两个概率,做如下实验,每次取一枚硬币,连掷5次,记录下结果,这里每次试验的硬币为一随机变量,连掷5次,每次对应一个随机变量,详细信息如下:
。为了估计这两个概率,做如下实验,每次取一枚硬币,连掷5次,记录下结果,这里每次试验的硬币为一随机变量,连掷5次,每次对应一个随机变量,详细信息如下:
表1—硬币投掷试验
从表1可知,这个模型的数据都是可观察数据,根据这个试验结果,不难算出硬币1和2正面朝上的概率:

从表1可知,每个实验选择的是硬币1还是硬币2,是可观察数据,如果把抛掷硬币1或2正面朝上的概率作为参数 ,也可以极大似然估计的方法得到。
,也可以极大似然估计的方法得到。
这个通过求极大似然估计得到的参数与前面用通常计算频率的完全一致。
如果不告诉你每次投掷的是哪个硬币,或不知道每次投掷的是哪个硬币,此时,每次投掷的是哪个硬币就是一个无法观察的数据,这个数据我们通常称作为隐变量。用隐变量z表示没观察数据,其它各项不变。表1就变成表2的格式。表2—含隐含变量z的硬币投掷试验

5.3.2 EM算法

5.3.3 EM算法简单实例
5.3.4 EM算法推导
5.3.5 EM算法的收敛性
5.3.6从变分推断看EM算法
5.3.7 为何选择变分函数p(z│x,θ)作为逼近分布,而不是其它函数?
5.3.8 EM算法应用于k-means聚类
5.3.9 EM算法应用于高斯混合模型
5.3.10 EM算法核心思想
EM算法是一类算法,该算法核心是解决了带隐变量的参数估计。通过迭代的方法求参数的极大似然估计。具体步骤为:
(1)初始化参数 ;
;
(2)构建含隐变量的目标函数,如 函数,或欧氏距离等。
函数,或欧氏距离等。
(3)求目标函数的极值,得到参数
重复第(2)和(3)步,直到收敛或指定迭代次数。
极大似然估计和EM算法,与其说是一种算法,不如说是一种解决的框架,如拉格朗日乘数法、蒙特卡洛算法等一样,针对特定场景的特定算法,和线性回归,逻辑回归,决策树等一些具体的算法不同,极大似然和EM算法更加宽泛,是很多具体算法的基础。
5.3.11 EM算法的应用场景
EM算法的应用场景,一般而言,就是处理含有隐变量的极大似然估计问题,具体可分为以下一些具体情况:
1、存在缺失数据:缺失数据包括类别标签或缺失某些特征的值等情况。
2、无监督学习:聚类:对个样本所属族作为隐变量
3、隐马尔科夫模型:训练隐马尔科夫模型中的参数
4、运用在语言模型上:对文本进行分类
5、生成模型(VAE,GAN等)中应用
6、Gibbs采样中应用
5.3.12 EM算法的推广
5.2 极大后验概率估计
极大似然估计将参数θ看作是确定值,但其值未知,即是一个普通变量,是属于频率派,与频率派相对应的就是贝叶斯派,极大后验概率、EM算法等属于贝叶斯派。
5.2.1频率派与贝叶斯派的区别
关于参数估计,统计学界的两个学派分别提供了两种不同的解决方案。
频率派认为参数虽然未知,但是客观存在的固定值,通过优化似然函数等准则来确定其值。
贝叶斯派认为参数是未观察到的随机变量,其本身也可有分布,因此,可假定参数服从一个先验分布,然后基于观测到的数据来计算参数的后验分布,比如极大后验概率。
5.2.2经验风险最小化与结构风险最小化
经验风险最小化与结构风险最小化是对于损失函数而言的。可以说经验风险最小化只侧重训练数据集上的损失降到最低;而结构风险最小化是在经验风险最小化的基础上约束模型的复杂度,使其在训练数据集的损失降到最低的同时,模型不至于过于复杂,相当于在损失函数上增加了正则项,防止模型出现过拟合状态。这一点也符合奥卡姆剃刀原则-简单就是美。
经验风险最小化可以看作是采用了极大似然的参数评估方法,更侧重从数据中学习模型的潜在参数,而且是只看重数据样本本身。这样在数据样本缺失的情况下,模型容易发生过拟合的状态。
而结构风险最小化为了防止过拟合而提出来的策略。过拟合问题往往是由于训练数据少和噪声以及模型能力强等原因造成的。为了解决过拟合问题,一般在经验风险最小化的基础上再引入参数的正则化,来限制模型能力,使其不要过度地最小化经验风险。
在参数估计中,结构风险最小化采用了最大后验概率估计的思想来推测模型参数,不仅仅是依赖数据,还依靠模型参数的先验分布。这样在数据样本不是很充分的情况下,我们可以通过模型参数的先验分布,辅助以数据样本,做到尽可能的还原真实模型分布。
根据大数定律,当样本容量较大时,先验分布退化为均匀分布,称为无信息先验,最大后验估计退化为最大似然估计。
5.2.3 极大大后验概率估计
极大后验概率估计将参数θ视为随机变量,并假设它服从某种概率分布。通过最大化后验概率 来确定其值。即在样本出现的情况条件下,最大化参数的后验概率。求解时需要假设参数
来确定其值。即在样本出现的情况条件下,最大化参数的后验概率。求解时需要假设参数 服从某种分布,这个分布需要预先知道,故又称为先验概率。
服从某种分布,这个分布需要预先知道,故又称为先验概率。
假设参数 服从分布的概率函数为
服从分布的概率函数为 根据贝叶斯公式,参数
根据贝叶斯公式,参数 对已知样本的后验概率为:
对已知样本的后验概率为:

考虑到其中概率p(x)与参数 无关,所以,最大化后验概率
无关,所以,最大化后验概率 等价于最大化
等价于最大化 ,即:
,即:

由此可得极大后验概率的对数似然估计为:

式(5.5)比式(5.2)多了 这项,如果参数
这项,如果参数 服从均匀分布,即其概率函数为一个常数,则最大化后验概率估计与最大化参数估计一致。或者,也可以反过来,认为MLE是把先验概率
服从均匀分布,即其概率函数为一个常数,则最大化后验概率估计与最大化参数估计一致。或者,也可以反过来,认为MLE是把先验概率 认为等于1,即认为
认为等于1,即认为 是均匀分布。
是均匀分布。
例1:假设n个样本,它们属于伯努利分布B(p),其中取值为1的样本有m个,取值为0的样本有n-m个,假设参数p服从正态分布N(0.3,0.01),样本集的极大后验概率函数为: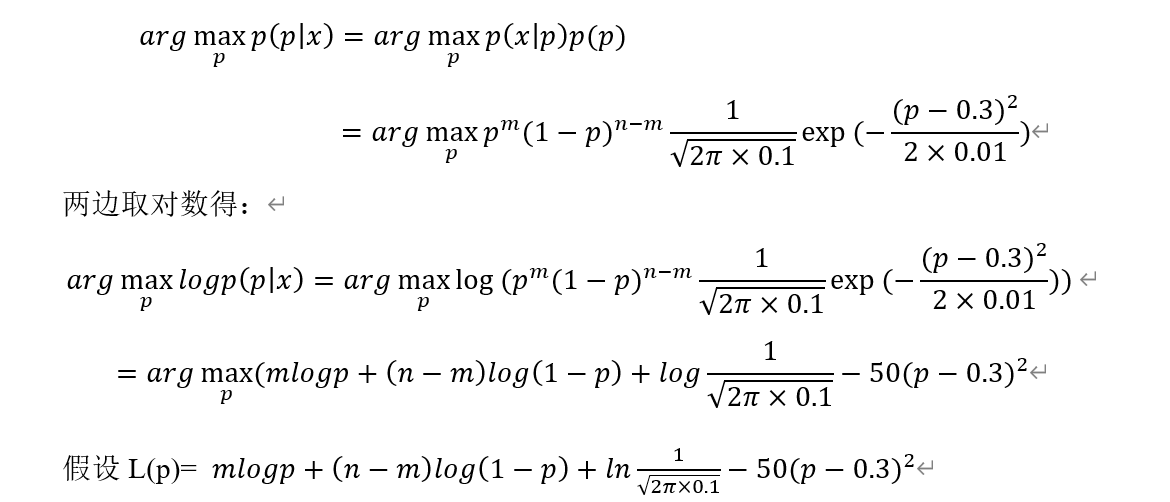
为求L(p)的最大值,对其求导,并令导数为0,可得:

其中0<p<1,当n=100,m=30时,可解得:
p=0.3
这个值与极大似然估计的计算的值一样。
5.2.4 极大后验概率估计的应用
极大后验概率估计与极大似然估计相比,多了一个先验概率 ,通过这个先验概率可以给模型增加一些正则约束。假设模型的参数
,通过这个先验概率可以给模型增加一些正则约束。假设模型的参数 服从正太分布。
服从正太分布。

其中正态分布的参数 为已知。由式(5.6)可知,随机变量
为已知。由式(5.6)可知,随机变量 的极大后验概率估计为
的极大后验概率估计为

其中
在极大似然估计的基础上加了正态分布的先验,这等同于在已有的损失函数上加了L2正则。
可以看出,最大后验概率等价于平方损失的结构风险最小化。