文章目录
- 第12章 TensorFlow卷积神经网络
- 12.1 卷积神经网络简介
- 12.2卷积的定义
- 12.3卷积运算
- 12.4 卷积网络结构
- 12.4.1卷积层
- 12.4.2激活函数
- 12.4.3池化层(Pooling)
- 12.4.4归一化层
- 12.4.5全连接层
- 12.4.6几种经典的CNN
- 12.4.6.1 LeNet5
- 12.4.6.2 AlexNet
- 12.4.6.3 VGGNet
- 12.4.6.4Google Inception Net
- 12.4.6.5 ResNet
- 12.4.6.6 CNN发展趋势
- 12.5 卷积网络TensorFlow实例
- 12.5.1 网络架构图
- 12.5.2卷积层
- 12.5.3导入需要的包
- 12.5.4 定义网络参数
- 12.5.5 导入数据
- 12.5.6 把标签转换为one-hot格式
- 12.5.7 数据维度
- 12.5.8打印部分样例图片
- 12.5.9 CNN的Tensorflow实现
- 12.5.9.1 创建变量
- 12.5.9.2 创建卷积
- 12.5.9.3 展平操作
- 12.5.9.4 创建全连接层
- 12.5.9.5 定义占位符
- 12.5.9.6 定义卷积层1
- 12.5.9.7 定义卷积层2
- 12.5.9.8 定义展平层
- 12.5.9.9 定义全连接层1
- 12.5.9.10 预测类别
- 12.5.9.12 选择优化方法
- 12.5.9.13 模型性能度量
- 12.5.10.2执行优化的帮助函数
- 12.5.10.3执行优化的帮助函数
- 12.5.10.4显示性能的帮助函数
- 12.5.10.5执行一轮优化后的性能
- 12.5.10.7 1000轮优化后的性能
- 12.5.10.8 10000轮优化后的性能
- 12.5.11权重和层的可视化
- 12.5.11.1卷积权重可视化
- 12.5.11.2卷积层输出可视化
- 12.5.11.3打印输入图像
- 12.5.11.4显示卷积层1的权重
第12章 TensorFlow卷积神经网络
12.1 卷积神经网络简介
卷积神经网路(Convolutional Neural Network, CNN)是一种前馈神经网络,对于CNN最早可以追溯到1986年BP算法的提出,1989年LeCun将其用到多层神经网络中,直到1998年LeCun提出LeNet-5模型,神经网络的雏形基本形成。在接下来近十年的时间里,卷积神经网络的相关研究处于低谷,原因有两个:一是研究人员意识到多层神经网络在进行BP训练时的计算量极其之大,当时的硬件计算能力完全不可能实现;二是包括SVM在内的浅层机器学习算法也渐渐开始暂露头脚。
2006年,Hinton终于一鸣惊人,在《科学》上发表文章,CNN再度觉醒,并取得长足发展。2012年,ImageNet大赛上CNN夺冠,2014年,谷歌研发出20层的VGG模型。同年,DeepFace、DeepID模型横空出世,直接将LFW数据库上的人脸识别、人脸认证的正确率刷到99.75%,几乎超越人类。
卷积神经网路由一个或多个卷积层和顶端的全连通层(对应经典的神经网路)组成,同时也包括关联权重和池化层(pooling layer)。这一结构使得卷积神经网路能够利用输入数据的二维结构。与其他深度学习结构相比,卷积神经网路在图像和语音识别方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。相比较其他深度、前馈神经网路,卷积神经网路需要考量的参数更少,使之成为一种颇具吸引力的深度学习结构。
12.2卷积的定义
卷积现在可能是深度学习中最重要的概念。正是靠着卷积和卷积神经网络,深度学习才超越了几乎其他所有的机器学习方法。要理解卷积神经网络,首先需要了解卷积的含义,卷积的定义有点抽象,我们先给出一个数学上的定义,然后通过一个简单例子及其物理意义来帮助大家理解。
卷积(Convolution)是一种数学运算,它是通过两个函数f和g生成第三个函数的一种运算或数学操作。卷积的数据定义为:
其离散定义为:

通常把函数g称为输入函数,函数f称为滤波器(Filter),或卷积核(kernel),得到的结果h为特征图或特征映射(feature map)。
数学上的定义有点抽象,下面我通过几个示例来帮助大家理解。
1)小李定期存款示例
小李存入100元钱,年利率是4%,按本息计算(即将每一年所获利息加入本金,以计算下一年的利息),那么在五年之后他能拿到的钱数是:

以此类推,如果小李每年都往银行中存入新的100元钱,那么这个收益表格将是这样的:

在上式中,f(t)为小李的存钱函数,而g(t)为存入银行的每一笔钱的本息计算函数。在这里,小李最终得到的钱就是他的存钱函数和本息计算函数的卷积。
如果我们把这个公式推广到连续的情况,也就是说,小李在从0到x的这一段时间内,每时每刻都往银行里存钱,他的存钱函数为
f(t) (0≤t≤x)
而银行也对他存入的每一笔钱按本息公式计算收益:

通过上面这个例子,大家应该能够很清晰地记住卷积公式了。
如果我们将小李的存款函数视为一个信号发生(也就是激励)的过程,而将本息函数
g(x-t)
视为一个系统对信号的响应函数(也就是响应),那么二者的卷积
(f*g)(x)
就可以看做是在x时刻对系统进行观察,得到的观察结果(也就是输出)将是过去产生的所有信号经过系统的处理后得到的结果的叠加或加权平均,这也就是卷积的物理意义了。
参考了:https://www.zhihu.com/question/21686447
2)两个方形脉冲波的卷积示例
下图为两个方形脉冲波的卷积。其中函数"g"首先对τ=0反射,接着平移"t",成为 g(t-τ)。那么重叠部分的面积就相当于"t"处的卷积,其中横坐标代表待变量τ 以及新函数f*g的自变量"t"。

图1 两个方形脉冲的卷积
下图示方形脉冲波和指数衰退的脉冲波的卷积(后者可能出现于RC电路中),同样地重叠部分面积就相当于"t"处的卷积。注意到因为"g"是对称的,所以在这两张图中,反射并不会改变它的形状。

图2 一个方形与指数衰退的脉冲波的卷积
该图取自:
https://zh.wikipedia.org/wiki/%E5%8D%B7%E7%A7%AF
12.3卷积运算
上节我们通过一些简单示例介绍了卷积的定义,卷积本质上是一个线性运算,因此卷积操作也被称为线性滤波。卷积如何运算?为提供一个直观印象,我们先看一个简单的二维空间卷积运算示例:
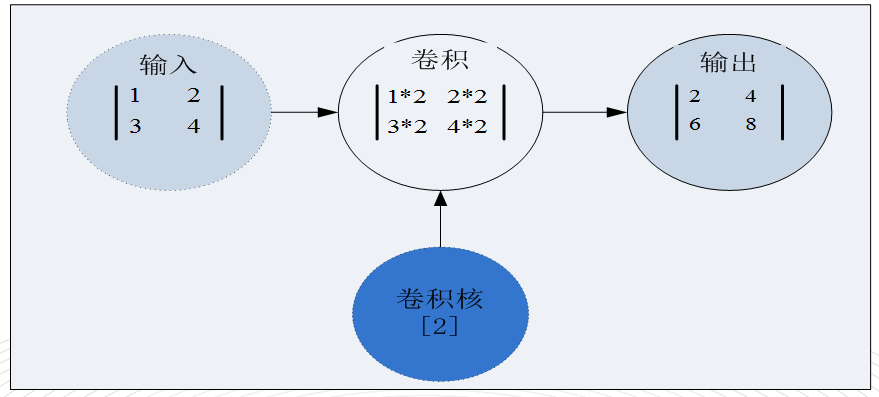
这个二维空间的卷积运算对两个输入张量(即输入和卷积核)进行卷积,并把结果输出。
接下来再看一个二维卷积详细运算过程,以便于大家对卷积运算有个更全面的了解。

图3 卷积运算
该图取自:https://www.zybuluo.com/hanbingtao/note/485480
在以上计算中,输入为一个5x5的矩阵,移动窗口为3x3矩阵,又称为卷积矩阵或卷积核,这个矩阵值为共享参数,移动步长或步幅(stride)为1,当然这个值可以大于1,如2或3等。小窗口移动过程中,其中的值是保持不变的:

图4 卷积核
这就是参数共享的说法,这些参数就决定一个卷积核,每个卷积核能够提取某一部分的特征。一般情况下,只有一个卷积核是不够的,在实际处理中,往往通过多个卷积核来提取多重特征,每一个卷积核与原始输入数据执行卷积操作后得到一个特征映射,如下图:

上图中,最右边,特征映射矩阵中的4,具体计算公式如下:


上图中,最右边特征映射矩阵中的3,具体计算公式如下:
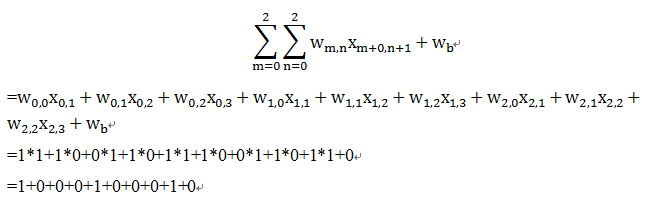
其他以此类推,最后输出结果为:
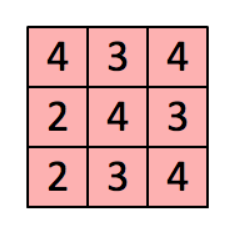
图5 输出结果
以上介绍了一个输入,通过一个卷积核后,得到一个特征映射。如果输入有多个,卷积核也有多个情况又如何呢?另外,步幅也可以是大于1的整数,如为2,如果原来的输入为5*5的矩阵,卷积核还是3*3的矩阵,那么卷积核小窗口按步幅2从左到右,从上到下移动过程中,可能导致卷积核窗口部分在输入矩阵之外,如下图:
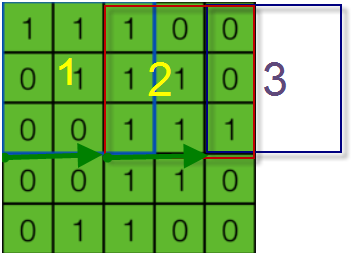
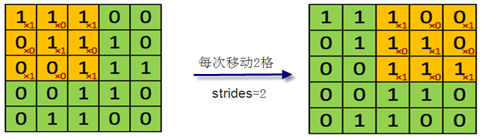
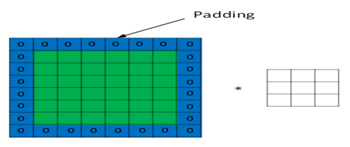
当卷积窗口在3这个位置时,它只覆盖输入矩阵的一列,这个时候该如何处理呢?为防止信息丢失,我们采用边界外面补0(Zero padding)策略。下面的动画显示了包含两个卷积核的卷积层的计算。我们可以看到7*7*3输入,经过两个3*3*3的卷积(步幅为2),得到了3*3*2的输出。另外我们也会看到下图的Zero padding是1,也就是在输入元素的周围补了一圈0。Zero padding对于图像边缘部分的特征提取是很有帮助的,可以防止信息丢失。

图6 多个输入及卷积核的卷积计算
以上就是卷积层的计算方法。这里面体现了局部连接和权值共享:每层神经元只和上一层部分神经元相连(卷积计算规则),且卷积核的权值对于上一层所有神经元都是一样的。对于包含两个3*3*3的卷积核的卷积层来说,其参数数量仅有(3*3*3+1)*2=56个,且参数数量与上一层神经元个数无关。与全连接神经网络相比,其参数数量大大减少了。
这是通常的卷积运算,此外,还有多种卷积运算,如空洞卷积、分离卷积等等,这里我们介绍一下空洞卷积(atrous convolutions),空洞卷积又称为扩张卷积(dilated convolutions),向卷积层引入了一个称为 “扩张率(dilation rate)”的新参数,该参数定义了卷积核处理数据时各值的间距。

卷积核为3、扩张率为2和无边界扩充的二维空洞卷积
一个扩张率为2的3×3卷积核,感受野与5×5的卷积核相同,而且仅需要9个参数。你可以把它想象成一个5×5的卷积核,每隔一行或一列删除一行或一列。
在相同的计算条件下,空洞卷积提供了更大的感受野。空洞卷积经常用在实时图像分割中。当网络层需要较大的感受野,但计算资源有限而无法提高卷积核数量或大小时,可以考虑空洞卷积。
卷积核,从这个名字可以看出它的重要性,它是整个卷积过程的核心。比较简单的卷积核或过滤器有Horizontalfilter、Verticalfilter、Sobel filter等。这些过滤器能够检测图像的水平边缘、垂直边缘、增强图片中心区域权重等。

12.4 卷积网络结构
卷积神经网络到底啥样?为获取一个感性认识,我们先看一下卷积神经网络的示意图。

图7 卷积神经网络
由图7可知,一个卷积神经网络由若干卷积层(Convolution)、池化层(Pooling)、全连接层(fully connected)组成。
从图7我们可以发现卷积神经网络的层结构和全连接神经网络的层结构有很大不同。全连接神经网络每层的神经元是按照一维排列的,也就是排成一条线的样子;而卷积神经网络每层的神经元是按照三维排列的,也就是排成一个长方体的样子,有宽度、高度和深度。
对于图7展示的神经网络,我们看到输入层的宽度和高度对应于输入图像的宽度和高度,而它的深度为1。接着,第一个卷积层对这幅图像进行了卷积操作,得到了三个特征映射。这里的"3"可能是让很多初学者迷惑的地方,实际上,就是这个卷积层包含三个卷积核,也就是三套参数(或共享参数),每个卷积核都可以把原始输入图像卷积得到一个特征映射,三个卷积核就可以得到三个特征映射。至于一个卷积层可以有多少个卷积核,那是可以自由设定的。也就是说,卷积层的卷积核个数也是一个超参数。我们可以把特征映射可以看做是通过卷积变换提取到的图像特征,三个卷积核就对原始图像提取出三组不同的特征,也就是得到了三个特征映射,也称做三个通道(channel)。
继续观察图7,在第一个卷积层之后,Pooling层对三个特征映射做了下采样,得到了三个更小的特征映射。接着,是第二个卷积层,它有5个卷积核。每个卷积核都把前面下采样之后的3个**特征映射卷积在一起,得到一个新的特征映射。这样,5个卷积核就得到了5个特征映射。接着,是第二个Pooling,继续对5个特征映射进行下采样,得到了5个更小的特征映射。
图7所示网络的最后两层是全连接层。第一个全连接层的每个神经元,和上一层5个特征映射中的每个神经元相连,第二个全连接层(也就是输出层)的每个神经元,则和第一个全连接层的每个神经元相连,这样得到了整个网络的输出。
至此,我们对卷积神经网络有了最基本的感性认识。接下来,我们将介绍卷积神经网络中各种层的计算和训练。
12.4.1卷积层
我们知道一般神经网络没有卷积层,深度学习中的卷积层能解决哪些问题?
神经网络在处理图像时数据量太大,例如一个输入1000*1000像素的图片(一百万像素,现在已经不能算大图了),输入层有1000*1000=100万节点。假设第一个隐藏层有100个节点(这个数量并不多),那么仅这一层就有(1000*1000+1)*100=1亿参数,这实在是太多了!神经网络训练本来就慢,这么多数据是不合理的。我们看卷积如何解决这个问题。
主要从三个方面:
局部连接
这个是最容易想到的,每个神经元不再和上一层的所有神经元相连,而只和一小部分神经元相连。这样就减少了很多参数。
权值共享
一组连接可以共享同一个权重,而不是每个连接有一个不同的权重,这样又减少了很多参数。
池化或下采样
可以使用Pooling来减少每层的样本数,进一步减少参数数量,同时还可以提升模型的鲁棒性。
对于图像识别任务来说,卷积神经网络通过尽可能保留重要的参数,去掉大量不重要的参数,来达到更好的学习效果
卷积核对图片进行卷积操作就得到的卷积层的输出,卷积核的大小是人为设定的,比如可以设置成3×3或其他尺寸,卷积核的个数也是人为设定,太多太少都不合适,卷积核的内容是训练的时候学习得来的,学习方法一般也是梯度下降法。
由上节内容可知,卷积操作,其实就是卷积核在输入的二维数据面上每次移动一个步长,进行乘法运算再除以卷积核的元素个数。
我们通常会使用多层卷积层来得到更深层次的特征图。如下:

12.4.2激活函数
为增强各层的表现力,各层的输出往往使用激活函数来生成特征映射或特征图,并以此来加入非线性因素的,因为线性模型的表达力不够。
在具体处理图像的时候,如何处理呢?我们知道在神经网络中,对于图像,我们主要采用了卷积的方式来处理,也就是对每个像素点赋予一个权值,这个操作显然就是线性的。但是样本不一定是线性可分的,为了解决这个问题,我们可以进行线性变化,或者我们引入非线性因素,解决线性模型所不能解决的问题。
在选择激活函数时应该满足注意哪些方面呢?
首先,我们知道神经网络的数学基础是处处可微的,所以选取的激活函数要能保证数据输入与输出也是可微的,运算特征是不断进行循环计算,所以在每代循环过程中,每个神经元的值也是在不断变化的。 这就导致了tanh特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果显示出来,但有时,在特征相差比较复杂或是相差不是特别大时,需要更细微的分类判断的时候,sigmoid效果就好了。
其次,sigmoid 和 tanh作为激活函数的话,一定要注意一定要对 input 进行归一话,否则激活后的值都会进入平坦区,使隐层的输出全部趋同,但是 ReLU 并不需要输入归一化来防止它们达到饱和。
此外,对稀疏矩阵,也就是大多数为0的稀疏矩阵来表示。这个特性矩阵比较适合采用于Relu激活函数,Relu就是取的max(0,x),因为神经网络是不断反复计算,实际上变成了它在尝试不断试探如何用一个大多数为0的矩阵来尝试表达数据特征,结果因为稀疏特性的存在,反而这种方法变得运算得又快效果又好了。所以我们可以看到目前大部分的卷积神经网络中,基本上都是采用了ReLU 函数。
常用的激活函数
激活函数应该具有的性质:
(1)非线性。线性激活层对于深层神经网络没有作用,因为其作用以后仍然是输入的各种线性变换。。
(2)连续可微。梯度下降法的要求。
(3)范围最好不饱和,当有饱和的区间段时,若系统优化进入到该段,梯度近似为0,网络的学习就会停止。
(4)单调性,当激活函数是单调时,单层神经网络的误差函数是凸的,好优化。
(5)在原点处近似线性,这样当权值初始化为接近0的随机值时,网络可以学习的较快,不用可以调节网络的初始值。
目前常用的激活函数都只拥有上述性质的部分,没有一个拥有全部。
下面介绍几种常用的激活函数。

目前已被淘汰 ,其主要缺点:
饱和时梯度值非常小。由于BP算法反向传播的时候后层的梯度是以乘性方式传递到前层,因此当层数比较多的时候,传到前层的梯度就会非常小,网络权值得不到有效的更新,即梯度消失。如果该层的权值初始化使得f(x) 处于饱和状态时,网络基本上权值无法更新。
Tanh函数
Tanh和Sigmoid是有异曲同工之妙的,它的图形如上图右所示,不同的是它把实值得输入压缩到-1~1的范围,因此它基本是0均值的,也就解决了上述Sigmoid缺点中的第二个,所以实际中tanh会比sigmoid更常用。但是它还是存在梯度饱和的问题。Tanh是sigmoid的变形:
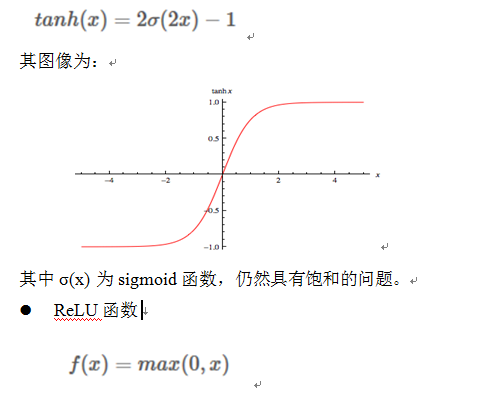

Alex在2012年提出的一种新的激活函数。该函数的提出很大程度的解决了BP算法在优化深层神经网络时的梯度耗散问题 。
优点:
(1) x>0 时,梯度恒为1,无梯度耗散问题,收敛快;
(2)增大了网络的稀疏性。当x (3)运算量很小;
缺点:
如果后层的某一个梯度特别大,导致W更新以后变得特别大,导致该层的输入<0,输出为0,这时该层就会‘die’,没有更新。当学习率比较大时可能会有40%的神经元都会在训练开始就‘die’,因此需要对学习率进行一个好的设置。
由优缺点可知max(0,x) 函数为一个双刃剑,既可以形成网络的稀疏性,也可能造成有很多永远处于‘die’的神经元,需要tradeoff。

改善了ReLU的死亡特性,但是也同时损失了一部分稀疏性,且增加了一个超参数,目前来说其好处不太明确

根据一定的概率(可配置)将输出设置为0,当引入少量随机性将有助于训练时,这个层有很好的表现,它是防止过拟合的一种策略,Dropout在训练的时候有,但在测试的时候是不能有Dropout的,毕竟只有在训练学习的时候才才担心过拟合。
简单讲,Dropout就是在按梯度下降法求网络参数的时候,每一次迭代都随机删掉一些隐含神经元,注意删掉之后会再次放回,下次迭代继续在所有隐含神经元存在的情况下随机删除。
解决过拟合的方法还有在代价函数添加正则项的方法,L1是添加绝对值,L2是添加二次方差。这两个正则项在数学上是可以证明的,能防止参数w过大。
那Dropout为什么有助于防止过拟合呢?可以简单地这样解释,运用了dropout的训练过程,相当于训练了很多个只有半数隐层单元的神经网络(后面简称为“半数网络”),每一个这样的半数网络,都可以给出一个分类结果,这些结果有的是正确的,有的是错误的。随着训练的进行,大部分半数网络都可以给出正确的分类结果,那么少数的错误分类结果就不会对最终结果造成大的影响。实际上dropout不一定非要在全连接层隐含层,卷积似乎也可以dropout。
如何选择激活函数?
通常来说,很少会把各种激活函数串起来在一个网络中使用的。
如果使用 ReLU,那么一定要小心设置 learning rate,而且要注意不要让你的网络出现很多 “dead” 神经元,如果这个问题不好解决,那么可以试试 Leaky ReLU、PReLU 或者 Maxout.
最好不要用 sigmoid,可以试试 tanh,不过可以预期它的效果会比不上 ReLU 和 Maxout。
实际使用的时候最常用的还是ReLU函数,注意学习率的设置以及死亡节点所占的比例即可。
12.4.3池化层(Pooling)
池化(Pooling)又称为下采样,通过卷积层获得了图像的特征之后,理论上我们可以直接使用这些特征训练分类器(如softmax),但是这样做将面临巨大的计算量的挑战,而且容易产生过拟合的现象。为了进一步降低网络训练参数及模型的过拟合程度,对卷积层进行池化/采样(Pooling)处理。池化/采样的方式通常有以下两种:
最大池化(Max Pooling: 选择Pooling窗口中的最大值作为采样值;
均值池化(Mean Pooling): 将Pooling窗口中的所有值相加取平均,以平均值作为采样值
高斯池化:借鉴高斯模糊的方法。不常用。
图像经过池化后,得到的是一系列的特征图,而多层感知器接受的输入是一个向量。因此需要将这些特征图中的像素依次取出,排列成一个向量。各种池化方法可用如下图来表示:

12.4.4归一化层
对于归一化我们应该不陌生,在线性回归和逻辑回归中经常使用,而且很有效。因为输入层的输入值的大小变化不剧烈,那么输入也不会。但是,对于一个可能有很多层的深度学习模型来说,情况可能会比较复杂。
举个例子,随着第一层和第二层的参数在训练时不断变化,第三层所使用的激活函数的输入值可能由于乘法效应而变得极大或极小,例如和第一层所使用的激活函数的输入值不在一个数量级上。这种在训练时可能出现的情况会造成模型训练的不稳定性。例如,给定一个学习率,某次参数迭代后,目标函数值会剧烈变化或甚至升高。数学的解释是,如果把目标函数 f根据参数 w迭代进行泰勒展开,有关学习率 η 的高阶项的系数可能由于数量级的原因(通常由于层数多)而不容忽略。然而常用的低阶优化算法(如梯度下降)对于不断降低目标函数的有效性通常基于一个基本假设:在以上泰勒展开中把有关学习率的高阶项通通忽略不计。
为了应对上述这种情况,Sergey Ioffe和Christian Szegedy在2015年提出了批量归一化(Batch Normalization, BN)的方法。简而言之,在训练时给定一个批量输入,批量归一化试图对深度学习模型的某一层所使用的激活函数的输入进行归一化:使批量呈标准正态分布(均值为0,标准差为1)。
批量归一化通常应用于输入层或任意中间层
12.4.5全连接层
全连接层(fully connected layers,FC)在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。在实际使用中,全连接层可由卷积操作实现:对前层是全连接的全连接层可以转化为卷积核为1x1的卷积;而前层是卷积层的全连接层可以转化为卷积核为hxw的全局卷积,h和w分别为前层卷积结果的高和宽。
目前由于全连接层参数冗余(仅全连接层参数就可占整个网络参数80%左右),近期一些性能优异的网络模型如ResNet和GoogLeNet等均用全局平均池化(global average pooling,GAP)取代FC来融合学到的深度特征,最后仍用softmax等损失函数作为网络目标函数来指导学习过程。需要指出的是,用GAP替代FC的网络通常有较好的预测性能。
近期的研究(In Defense of Fully Connected Layers in Visual Representation Transfer)发现,FC可在模型表示能力迁移过程中充当“防火墙”的作用。具体来讲,假设在ImageNet上预训练得到的模型为 ,则ImageNet可视为源域(迁移学习中的source domain)。微调(fine tuning)是深度学习领域最常用的迁移学习技术。针对微调,若目标域(target domain)中的图像与源域中图像差异巨大(如相比ImageNet,目标域图像不是物体为中心的图像,而是风景照,见下图),不含FC的网络微调后的结果要差于含FC的网络。因此FC可视作模型表示能力的“防火墙”,特别是在源域与目标域差异较大的情况下,FC可保持较大的模型capacity从而保证模型表示能力的迁移。
12.4.6几种经典的CNN
这里介绍几种经典的CNN,如LeNet5、AlexNet、VGGNet、Google Inception Net、ResNet等。
12.4.6.1 LeNet5
LeNet5 诞生于 1994 年,是最早的卷积神经网络之一,并且推动了深度学习领域的发展。自从 1988 年开始,在许多次成功的迭代后,这项由 Yann LeCun 完成的开拓性成果被命名为 LeNet5(参见:Gradient-Based Learning Applied to Document Recognition)。

图1
LeNet5 的架构基于这样的观点:(尤其是)图像的特征分布在整张图像上,以及带有可学习参数的卷积是一种用少量参数在多个位置上提取相似特征的有效方式。在那时候,没有 GPU 帮助训练,甚至 CPU 的速度也很慢。因此,能够保存参数以及计算过程是一个关键进展。这和将每个像素用作一个大型多层神经网络的单独输入相反。LeNet5 阐述了那些像素不应该被使用在第一层,因为图像具有很强的空间相关性,而使用图像中独立的像素作为不同的输入特征则利用不到这些相关性。
LeNet5特征能够总结为如下几点:
1)卷积神经网络使用三个层作为一个系列: 卷积,池化,非线性
2) 使用卷积提取空间特征
3)使用映射到空间均值下采样(subsample)
4)双曲线(tanh)或S型(sigmoid)形式的非线性
5)多层神经网络(MLP)作为最后的分类器
6)层与层之间的稀疏连接矩阵避免大的计算成本
总体看来,这个网络是最近大量神经网络架构的起点,并且也给这个领域带来了许多灵感。
12.4.6.2 AlexNet
2012年,Hinton的学生Alex Krizhevsky提出了深度卷积神经网络模型AlexNet,它可以算是LeNet的一种更深更宽的版本。AlexNet中包含了几个比较新的技术点,也首次在CNN中成功应用了ReLU、Dropout和LRN等Trick。同时AlexNet也使用了GPU进行运算加速,作者开源了他们在GPU上训练卷积神经网络的CUDA代码。AlexNet包含了6亿3000万个连接,6000万个参数和65万个神经元,拥有5个卷积层,其中3个卷积层后面连接了最大池化层,最后还有3个全连接层。AlexNet以显著的优势赢得了竞争激烈的ILSVRC 2012比赛,top-5的错误率降低至了16.4%,相比第二名的成绩26.2%错误率有了巨大的提升。AlexNet可以说是神经网络在低谷期后的第一次发声,确立了深度学习(深度卷积网络)在计算机视觉的统治地位,同时也推动了深度学习在语音识别、自然语言处理、强化学习等领域的拓展。
AlexNet将LeNet的思想发扬光大,把CNN的基本原理应用到了很深很宽的网络中。AlexNet主要使用到的新技术点如下。
(1)成功使用ReLU作为CNN的激活函数,并验证其效果在较深的网络超过了Sigmoid,成功解决了Sigmoid在网络较深时的梯度弥散问题。虽然ReLU激活函数在很久之前就被提出了,但是直到AlexNet的出现才将其发扬光大。
(2)训练时使用Dropout随机忽略一部分神经元,以避免模型过拟合。Dropout虽有单独的论文论述,但是AlexNet将其实用化,通过实践证实了它的效果。在AlexNet中主要是最后几个全连接层使用了Dropout。
(3)在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化,AlexNet全部使用最大池化,避免平均池化的模糊化效果。并且AlexNet中提出让步长比池化核的尺寸小,这样池化层的输出之间会有重叠和覆盖,提升了特征的丰富性。
(4)提出了LRN层,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。
(5)使用CUDA加速深度卷积网络的训练,利用GPU强大的并行计算能力,处理神经网络训练时大量的矩阵运算。AlexNet使用了两块GTX 580 GPU进行训练,单个GTX 580只有3GB显存,这限制了可训练的网络的最大规模。因此作者将AlexNet分布在两个GPU上,在每个GPU的显存中储存一半的神经元的参数。因为GPU之间通信方便,可以互相访问显存,而不需要通过主机内存,所以同时使用多块GPU也是非常高效的。同时,AlexNet的设计让GPU之间的通信只在网络的某些层进行,控制了通信的性能损耗。
(6)数据增强,随机地从256 x 256的原始图像中截取224 x 224大小的区域(以及水平翻转的镜像),相当于增加了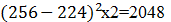 倍的数据量。如果没有数据增强,仅靠原始的数据量,参数众多的CNN会陷入过拟合中,使用了数据增强后可以大大减轻过拟合,提升泛化能力。进行预测时,则是取图片的四个角加中间共5个位置,并进行左右翻转,一共获得10张图片,对他们进行预测并对10次结果求均值。同时,AlexNet论文中提到了会对图像的RGB数据进行PCA处理,并对主成分做一个标准差为0.1的高斯扰动,增加一些噪声,这个Trick可以让错误率再下降1%。
倍的数据量。如果没有数据增强,仅靠原始的数据量,参数众多的CNN会陷入过拟合中,使用了数据增强后可以大大减轻过拟合,提升泛化能力。进行预测时,则是取图片的四个角加中间共5个位置,并进行左右翻转,一共获得10张图片,对他们进行预测并对10次结果求均值。同时,AlexNet论文中提到了会对图像的RGB数据进行PCA处理,并对主成分做一个标准差为0.1的高斯扰动,增加一些噪声,这个Trick可以让错误率再下降1%。
整个AlexNet有8个需要训练参数的层(不包括池化层和LRN层),前5层为卷积层,后3层为全连接层,如图4所示。AlexNet最后一层是有1000类输出的Softmax层用作分类。 LRN层出现在第1个及第2个卷积层后,而最大池化层出现在两个LRN层及最后一个卷积层后。ReLU激活函数则应用在这8层每一层的后面。因为AlexNet训练时使用了两块GPU,因此这个结构图中不少组件都被拆为了两部分。现在我们GPU的显存可以放下全部模型参数,因此只考虑一块GPU的情况即可。
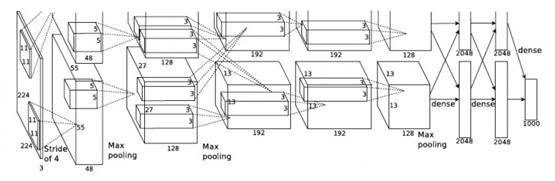
图4
AlexNet每层的超参数如图5所示。其中输入的图片尺寸为224x224,第一个卷积层使用了较大的卷积核尺寸11x11,步长为4,有96个卷积核;紧接着一个LRN层;然后是一个3 x 3的最大池化层,步长为2。这之后的卷积核尺寸都比较小,都是5 x 5或者3 x 3的大小,并且步长都为1,即会扫描全图所有像素;而最大池化层依然保持为3 x 3,并且步长为2。我们可以发现一个比较有意思的现象,在前几个卷积层,虽然计算量很大,但参数量很小,都在1M左右甚至更小,只占AlexNet总参数量的很小一部分。这就是卷积层有用的地方,可以通过较小的参数量提取有效的特征。而如果前几层直接使用全连接层,那么参数量和计算量将成为天文数字。虽然每一个卷积层占整个网络的参数量的1%都不到,但是如果去掉任何一个卷积层,都会使网络的分类性能大幅地下降。

图5
12.4.6.3 VGGNet
VGGNet是牛津大学计算机视觉组(Visual Geometry Group)和Google DeepMind公司的研究员一起研发的的深度卷积神经网络。VGGNet探索了卷积神经网络的深度与其性能之间的关系,通过反复堆叠3x3的小型卷积核和2x2的最大池化层,VGGNet成功地构筑了16~19层深的卷积神经网络。VGGNet相比之前state-of-the-art的网络结构,错误率大幅下降,并取得了ILSVRC 2014比赛分类项目的第2名和定位项目的第1名。同时VGGNet的拓展性很强,迁移到其他图片数据上的泛化性非常好。VGGNet的结构非常简洁,整个网络都使用了同样大小的卷积核尺寸(3x3)和最大池化尺寸(2x2)。到目前为止,VGGNet依然经常被用来提取图像特征。VGGNet训练后的模型参数在其官方网站上开源了,可用来在domain specific的图像分类任务上进行再训练(相当于提供了非常好的初始化权重),因此被用在了很多地方。
VGGNet论文中全部使用了3x3的卷积核和2x2的池化核,通过不断加深网络结构来提升性能。图6所示为VGGNet各级别的网络结构图,图7所示为每一级别的参数量,从11层的网络一直到19层的网络都有详尽的性能测试。虽然从A到E每一级网络逐渐变深,但是网络的参数量并没有增长很多,这是因为参数量主要都消耗在最后3个全连接层。前面的卷积部分虽然很深,但是消耗的参数量不大,不过训练比较耗时的部分依然是卷积,因其计算量比较大。这其中的D、E也就是我们常说的VGGNet-16和VGGNet-19。C很有意思,相比B多了几个1x1的卷积层,1x1卷积的意义主要在于线性变换,而输入通道数和输出通道数不变,没有发生降维。

图6

图7
VGGNet拥有5段卷积,每一段内有2~3个卷积层,同时每段尾部会连接一个最大池化层用来缩小图片尺寸。每段内的卷积核数量一样,越靠后的段的卷积核数量越多:64 – 128 – 256 – 512 – 512。其中经常出现多个完全一样的3x3的卷积层堆叠在一起的情况,这其实是非常有用的设计。如图8所示,两个3x3的卷积层串联相当于1个5x5的卷积层,即一个像素会跟周围5x5的像素产生关联,可以说感受野大小为5x5。而3个3x3的卷积层串联的效果则相当于1个7x7的卷积层。除此之外,3个串联的3x3的卷积层,拥有比1个7x7的卷积层更少的参数量,只有后者的。最重要的是,3个3x3的卷积层拥有比1个7x7的卷积层更多的非线性变换(前者可以使用三次ReLU激活函数,而后者只有一次),使得CNN对特征的学习能力更强。

图8
VGGNet在训练时有一个小技巧,先训练级别A的简单网络,再复用A网络的权重来初始化后面的几个复杂模型,这样训练收敛的速度更快。在预测时,VGG采用Multi-Scale的方法,将图像scale到一个尺寸Q,并将图片输入卷积网络计算。然后在最后一个卷积层使用滑窗的方式进行分类预测,将不同窗口的分类结果平均,再将不同尺寸Q的结果平均得到最后结果,这样可提高图片数据的利用率并提升预测准确率。同时在训练中,VGGNet还使用了Multi-Scale的方法做数据增强,将原始图像缩放到不同尺寸S,然后再随机裁切224x224的图片,这样能增加很多数据量,对于防止模型过拟合有很不错的效果。实践中,作者令S在[256,512]这个区间内取值,使用Multi-Scale获得多个版本的数据,并将多个版本的数据合在一起进行训练。图9所示为VGGNet使用Multi-Scale训练时得到的结果,可以看到D和E都可以达到7.5%的错误率。最终提交到ILSVRC 2014的版本是仅使用Single-Scale的6个不同等级的网络与Multi-Scale的D网络的融合,达到了7.3%的错误率。不过比赛结束后作者发现只融合Multi-Scale的D和E可以达到更好的效果,错误率达到7.0%,再使用其他优化策略最终错误率可达到6.8%左右,非常接近同年的冠军Google Inceptin Net。同时,作者在对比各级网络时总结出了以下几个观点。
(1)LRN层作用不大。
(2)越深的网络效果越好。
(3)1x1的卷积也是很有效的,但是没有3x3的卷积好,大一些的卷积核可以学习更大的空间特征。
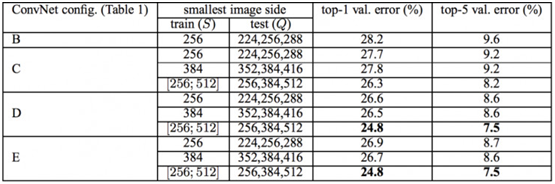
图9
12.4.6.4Google Inception Net
Google Inception Net首次出现在ILSVRC 2014的比赛中(和VGGNet同年),就以较大优势取得了第一名。那届比赛中的Inception Net通常被称为Inception V1,它最大的特点是控制了计算量和参数量的同时,获得了非常好的分类性能——top-5错误率6.67%,只有AlexNet的一半不到。Inception V1有22层深,比AlexNet的8层或者VGGNet的19层还要更深。但其计算量只有15亿次浮点运算,同时只有500万的参数量,仅为AlexNet参数量(6000万)的1/12,却可以达到远胜于AlexNet的准确率,可以说是非常优秀并且非常实用的模型。Inception V1降低参数量的目的有两点,第一,参数越多模型越庞大,需要供模型学习的数据量就越大,而目前高质量的数据非常昂贵;第二,参数越多,耗费的计算资源也会更大。Inception V1参数少但效果好的原因除了模型层数更深、表达能力更强外,还有两点:一是去除了最后的全连接层,用全局平均池化层(即将图片尺寸变为1x1)来取代它。全连接层几乎占据了AlexNet或VGGNet中90%的参数量,而且会引起过拟合,去除全连接层后模型训练更快并且减轻了过拟合。用全局平均池化层取代全连接层的做法借鉴了Network In Network(以下简称NIN)论文。二是Inception V1中精心设计的Inception Module提高了参数的利用效率,其结构如图10所示。这一部分也借鉴了NIN的思想,形象的解释就是Inception Module本身如同大网络中的一个小网络,其结构可以反复堆叠在一起形成大网络。不过Inception V1比NIN更进一步的是增加了分支网络,NIN则主要是级联的卷积层和MLPConv层。一般来说卷积层要提升表达能力,主要依靠增加输出通道数,但副作用是计算量增大和过拟合。每一个输出通道对应一个滤波器,同一个滤波器共享参数,只能提取一类特征,因此一个输出通道只能做一种特征处理。而NIN中的MLPConv则拥有更强大的能力,允许在输出通道之间组合信息,因此效果明显。可以说,MLPConv基本等效于普通卷积层后再连接1x1的卷积和ReLU激活函数。
我们再来看Inception Module的基本结构,其中有4个分支:第一个分支对输入进行1x1的卷积,这其实也是NIN中提出的一个重要结构。1x1的卷积是一个非常优秀的结构,它可以跨通道组织信息,提高网络的表达能力,同时可以对输出通道升维和降维。可以看到Inception Module的4个分支都用到了1x1卷积,来进行低成本(计算量比3x3小很多)的跨通道的特征变换。第二个分支先使用了1x1卷积,然后连接3x3卷积,相当于进行了两次特征变换。第三个分支类似,先是1x1的卷积,然后连接5x5卷积。最后一个分支则是3x3最大池化后直接使用1x1卷积。我们可以发现,有的分支只使用1x1卷积,有的分支使用了其他尺寸的卷积时也会再使用1x1卷积,这是因为1x1卷积的性价比很高,用很小的计算量就能增加一层特征变换和非线性化。Inception Module的4个分支在最后通过一个聚合操作合并(在输出通道数这个维度上聚合)。Inception Module中包含了3种不同尺寸的卷积和1个最大池化,增加了网络对不同尺度的适应性,这一部分和Multi-Scale的思想类似。早期计算机视觉的研究中,受灵长类神经视觉系统的启发,Serre使用不同尺寸的Gabor滤波器处理不同尺寸的图片,Inception V1借鉴了这种思想。Inception V1的论文中指出,Inception Module可以让网络的深度和宽度高效率地扩充,提升准确率且不致于过拟合。
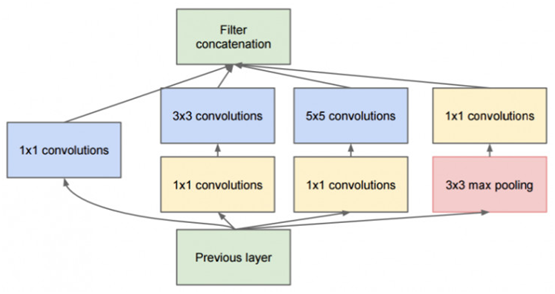
图10
人脑神经元的连接是稀疏的,因此研究者认为大型神经网络的合理的连接方式应该也是稀疏的。稀疏结构是非常适合神经网络的一种结构,尤其是对非常大型、非常深的神经网络,可以减轻过拟合并降低计算量,例如卷积神经网络就是稀疏的连接。Inception Net的主要目标就是找到最优的稀疏结构单元(即Inception Module),论文中提到其稀疏结构基于Hebbian原理,这里简单解释一下Hebbian原理:神经反射活动的持续与重复会导致神经元连接稳定性的持久提升,当两个神经元细胞A和B距离很近,并且A参与了对B重复、持续的兴奋,那么某些代谢变化会导致A将作为能使B兴奋的细胞。总结一下即“一起发射的神经元会连在一起”(Cells that fire together, wire together),学习过程中的刺激会使神经元间的突触强度增加。受Hebbian原理启发,另一篇文章Provable Bounds for Learning Some Deep Representations提出,如果数据集的概率分布可以被一个很大很稀疏的神经网络所表达,那么构筑这个网络的最佳方法是逐层构筑网络:将上一层高度相关(correlated)的节点聚类,并将聚类出来的每一个小簇(cluster)连接到一起,如图11所示。这个相关性高的节点应该被连接在一起的结论,即是从神经网络的角度对Hebbian原理有效性的证明。

图11
因此一个“好”的稀疏结构,应该是符合Hebbian原理的,我们应该把相关性高的一簇神经元节点连接在一起。在普通的数据集中,这可能需要对神经元节点聚类,但是在图片数据中,天然的就是临近区域的数据相关性高,因此相邻的像素点被卷积操作连接在一起。而我们可能有多个卷积核,在同一空间位置但在不同通道的卷积核的输出结果相关性极高。因此,一个1x1的卷积就可以很自然地把这些相关性很高的、在同一个空间位置但是不同通道的特征连接在一起,这就是为什么1x1卷积这么频繁地被应用到Inception Net中的原因。1x1卷积所连接的节点的相关性是最高的,而稍微大一点尺寸的卷积,比如3x3、5x5的卷积所连接的节点相关性也很高,因此也可以适当地使用一些大尺寸的卷积,增加多样性(diversity)。最后Inception Module通过4个分支中不同尺寸的1x1、3x3、5x5等小型卷积将相关性很高的节点连接在一起,就完成了其设计初衷,构建出了很高效的符合Hebbian原理的稀疏结构。
在Inception Module中,通常1x1卷积的比例(输出通道数占比)最高,3x3卷积和5x5卷积稍低。而在整个网络中,会有多个堆叠的Inception Module,我们希望靠后的Inception Module可以捕捉更高阶的抽象特征,因此靠后的Inception Module的卷积的空间集中度应该逐渐降低,这样可以捕获更大面积的特征。因此,越靠后的Inception Module中,3x3和5x5这两个大面积的卷积核的占比(输出通道数)应该更多。
Inception Net有22层深,除了最后一层的输出,其中间节点的分类效果也很好。因此在Inception Net中,还使用到了辅助分类节点(auxiliary classifiers),即将中间某一层的输出用作分类,并按一个较小的权重(0.3)加到最终分类结果中。这样相当于做了模型融合,同时给网络增加了反向传播的梯度信号,也提供了额外的正则化,对于整个Inception Net的训练很有裨益。
当年的Inception V1还是跑在TensorFlow的前辈DistBelief上的,并且只运行在CPU上。当时使用了异步的SGD训练,学习速率每迭代8个epoch降低4%。同时,Inception V1也使用了Multi-Scale、Multi-Crop等数据增强方法,并在不同的采样数据上训练了7个模型进行融合,得到了最后的ILSVRC 2014的比赛成绩——top-5错误率6.67%。
同时,Google Inception Net还是一个大家族,包括:
— 2014年9月的论文Going Deeper with Convolutions提出的Inception V1(top-5错误率6.67%)。
— 2015年2月的论文Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate提出的Inception V2(top-5错误率4.8%)。
— 2015年12月的论文Rethinking the Inception Architecture for Computer Vision提出的Inception V3(top-5错误率3.5%)。
— 2016年2月的论文Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning提出的Inception V4(top-5错误率3.08%)。
12.4.6.5 ResNet
2015 年 12 月又出现了新的变革,这和 Inception V3 出现的时间一样。ResNet 有着简单的思路:供给两个连续卷积层的输出,并分流(bypassing)输入进入下一层(参见论文:Deep Residual Learning for Image Recognition)。

图12
这和之前的一些旧思路类似。但 ResNet 中,它们分流两个层并被应用于更大的规模。在 2 层后分流是一个关键直觉,因为分流一个层并未给出更多的改进。通过 2 层可能认为是一个小型分类器,或者一个 Network-In-Network。
这是第一次网络层数超过一百,甚至还能训练出 1000 层的网络。
有大量网络层的 ResNet 开始使用类似于 Inception 瓶颈层的网络层:

图13
这种层通过首先是由带有更小输出(通常是输入的 1/4)的 1×1 卷积较少特征的数量,然后使用一个 3×3 的层,再使用 1×1 的层处理更大量的特征。类似于 Inception 模块,这样做能保证计算量低,同时提供丰富的特征结合。
ResNet 在输入上使用相对简单的初始层:一个带有两个池的 7×7 卷基层。可以把这个与更复杂、更少直觉性的 Inception V3、V4 做下对比。
ResNet 也使用一个池化层加上 softmax 作为最后的分类器。
关于 ResNet 的其他洞见每天都有发生:
ResNet 可被认为既是平行模块又是连续模块,把输入输出(inout)视为在许多模块中并行,同时每个模块的输出又是连续连接的。
ResNet 也可被视为并行模块或连续模块的多种组合(参见论文:Residual Networks are Exponential Ensembles of Relatively Shallow Networks)。
已经发现 ResNet 通常在 20-30 层的网络块上以并行的方式运行。而不是连续流过整个网络长度。
当 ResNet 像 RNN 一样把输出反馈给输入时,该网络可被视为更好的生物上可信的皮质模型(参见论文:Bridging the Gaps Between Residual Learning, Recurrent Neural Networks and Visual Cortex)。
12.4.6.6 CNN发展趋势
以上,我们简单回顾了卷积神经网络的历史,下图所示大致勾勒出最近几十年卷积神经网络的发展方向。
Perceptron(感知机)于1957年由Frank Resenblatt提出,而Perceptron不仅是卷积网络,也是神经网络的始祖。Neocognitron(神经认知机)是一种多层级的神经网络,由日本科学家Kunihiko Fukushima于20世纪80年代提出,具有一定程度的视觉认知的功能,并直接启发了后来的卷积神经网络。LeNet-5由CNN之父Yann LeCun于1997年提出,首次提出了多层级联的卷积结构,可对手写数字进行有效识别。
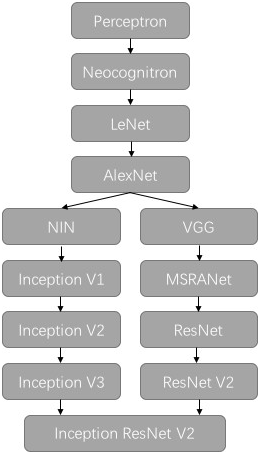
图14
可以看到前面这三次关于卷积神经网络的技术突破,间隔时间非常长,需要十余年甚至更久才出现一次理论创新。而后于2012年,Hinton的学生Alex依靠8层深的卷积神经网络一举获得了ILSVRC 2012比赛的冠军,瞬间点燃了卷积神经网络研究的热潮。AlexNet成功应用了ReLU激活函数、Dropout、最大覆盖池化、LRN层、GPU加速等新技术,并启发了后续更多的技术创新,卷积神经网络的研究从此进入快车道。
在AlexNet之后,我们可以将卷积神经网络的发展分为两类,一类是网络结构上的改进调整(图14左侧分支),另一类是网络深度的增加(图14右侧分支)。
2013年,颜水成教授的Network in Network工作首次发表,优化了卷积神经网络的结构,并推广了1x1的卷积结构。在改进卷积网络结构的工作中,后继者还有2014年的Google Inception Net V1,提出了Inception Module这个可以反复堆叠的高效的卷积网络结构,并获得了当年ILSVRC比赛的冠军。2015年初的Inception V2提出了Batch Normalization,大大加速了训练过程,并提升了网络性能。2015年年末的Inception V3则继续优化了网络结构,提出了Factorization in Small Convolutions的思想,分解大尺寸卷积为多个小卷积乃至一维卷积。
而另一条分支上,许多研究工作则致力于加深网络层数,2014年,ILSVRC比赛的亚军VGGNet全程使用3x3的卷积,成功训练了深达19层的网络,当年的季军MSRA-Net也使用了非常深的网络。2015年,微软的ResNet成功训练了152层深的网络,一举拿下了当年ILSVRC比赛的冠军,top-5错误率降低至3.46%。其后又更新了ResNet V2,增加了Batch Normalization,并去除了激活层而使用Identity Mapping或Preactivation,进一步提升了网络性能。此后,Inception ResNet V2融合了Inception Net优良的网络结构,和ResNet训练极深网络的残差学习模块,集两个方向之长,取得了更好的分类效果。
我们可以看到,自AlexNet于2012年提出后,深度学习领域的研究发展极其迅速,基本上每年甚至每几个月都会出现新一代的技术。新的技术往往伴随着新的网络结构,更深的网络的训练方法等,并在图像识别等领域不断创造新的准确率记录。至今,ILSVRC比赛和卷积神经网络的研究依然处于高速发展期,CNN的技术日新月异。当然其中不可忽视的推动力是,我们拥有了更快的GPU计算资源用以实验,以及非常方便的开源工具(比如TensorFlow)可以让研究人员快速地进行探索和尝试。在以前,研究人员如果没有像Alex那样高超的编程实力能自己实现cuda-convnet,可能都没办法设计CNN或者快速地进行实验。现在有了TensorFlow,研究人员和开发人员都可以简单而快速地设计神经网络结构并进行研究、测试、部署乃至实用。
参考:http://blog.csdn.net/app_12062011/article/details/62886113
12.5 卷积网络TensorFlow实例
在梯度下降和最优化部分我们用传统的神经网络在MNIST数据集上得到了90%左右的测试准确率。这个结果其实并不太理想。
在本章中,我们将使用卷积神经网络来得到一个准确率更高的模型,接近99%。卷积神经网络使用共享的卷积核对图像进行卷积操作,以提取图像深层特征。这些深层特征然后组合成特征向量输入全连接的神经网络中,再使用类似传统神经网络的方法进行分类。
12.5.1 网络架构图
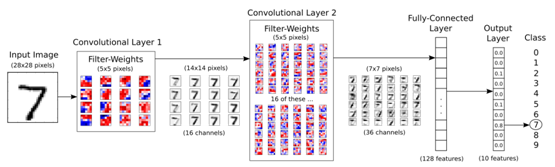
输入为原始的28x28的图像,它首先进入第一个拥有16个5x5卷积核的卷积层,得到16张28x28的卷积后的图像,再进入降采样层(图中省略)最终得到16张14x14的图像(可称为16个通道)。为了保证卷积前后图像的像素不变,在卷积过后,对图像边框采取补零的操作(在TensorFlow中的conv2d的padding参数为’SAME’,如果不采取补零而是缩小像素值,padding参数值设置为’VALID’)。降采样层使用max pooling操作,将2x2的像素块取最大值合并为一个像素点,这个操作会将图像缩小1倍。
对于得到的16通道的14x14图像,进入第二个拥有36个卷积核的卷积层,得到36张14x14的卷积后图像,再进入降采样层得到36张7x7的图像。在这里包括了一些隐含的操作,对于16张原始图像,每一张图像使用36个卷积核卷积,应该得到16x36张新的图像,但是为了减少模型的参数量,降低复杂度,卷积层对每个卷积核得到的16张图像相加,最后得到36张卷积后图像。
经过两层卷积后,将36张7x7的图像展平,得到一个7x7x36的向量,输入到一个128维的全连接层,最后输入到10维的softmx层进行分类。
这里层数较多,但关键是卷积层,下节我们重点介绍一下卷积层的运算逻辑。
12.5.2卷积层
卷积层使用多个卷积核作用于同一幅图像,以得到多个卷积后的图像。如下图所示:
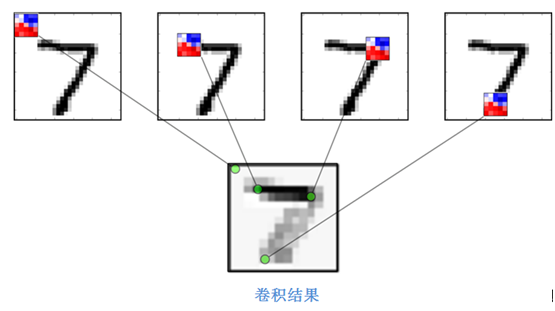
对于原始的图像7,使用一个5x5的卷积核,从左到右从上到下滑动。滑动的过程称为stride,卷积核分别从上到下,从左到右,步长一般设定为1或2。对卷积核覆盖的区域于卷积核进行点乘操作得到一个值作为该区域的中心点的像素。在上图中,红色代表这部分的像素对原始图像存在一个正的影响,而蓝色表示负的影响,在这个样例中卷积核似乎在识别图像中的横线部分,因为从结果看来7的那一横具有更强烈的反应。
此外,对于每一个卷积层的输出,一般会经过一个relu层或激活层,以保证全部的像素值都为正(因为所有为负的像素值都被设定为0),同时增强模型的泛化能力。
12.5.3导入需要的包
|
1 2 3 4 5 6 7 8 9 10 11 |
import tensorflow as tf import matplotlib.pyplot as plt import numpy as np from sklearn.metrics import confusion_matrix # 混淆矩阵,分析模型误差 import time # 计时 from datetime import timedelta import math #使用notebook在线画图 %matplotlib inline |
12.5.4 定义网络参数
|
1 2 3 4 5 6 7 8 9 10 |
# 卷积层 1 filter_size1 = 5 # 5 x 5 卷积核 num_filters1 = 16 # 共 16 个卷积核 # 卷积层 2 filter_size2 = 5 # 5 x 5 卷积核 num_filters2 = 36 # 共 36 个卷积核 # 全连接层. fc_size = 128 # 全连接层神经元个数. |
12.5.5 导入数据
TensorFlow在样例教程中已经做了下载并导入MNIST数字手写体识别数据集的实现,可以直接使用。但运行时经常发生断网或无法下载的情况,所以这里我们采用先从http://yann.lecun.com/exdb/mnist/下载,然后把下载的4个文件放在本地当前运行目录的data/mnist目录下,具体实现请看如下代码。其中load_mnist函数请参考梯度下降及优化部分。
|
1 2 3 4 5 6 7 8 9 |
X_train, y_train = load_mnist('./data/mnist', kind='train') print('Rows: %d, columns: %d' % (X_train.shape[0], X_train.shape[1])) X_test, y_test = load_mnist('./data/mnist', kind='t10k') print('Rows: %d, columns: %d' % (X_test.shape[0], X_test.shape[1])) print(y_train[:5],y_test[:5]) Rows: 60000, columns: 784 Rows: 10000, columns: 784 [5 0 4 1 9] [7 2 1 0 4] |
12.5.6 把标签转换为one-hot格式
从以上结果我们可以看出,目前标签值是0-9之间的数字,在机器学习或深度学习中,为提高分类的性能,一般会把类别转换one-hot的格式,这种格式把每个数字或类别转换为一个长度为类别总数的向量,一行只有一个1其余都是0。这里类别总数为10(共有10个不同的数字),7这个数字one-hot后就变成:[0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ],具体实现如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
def dense_to_one_hot(labels_dense, num_classes=10): """把类标签转换 one-hot向量.""" num_labels = labels_dense.shape[0] index_offset = np.arange(num_labels) * num_classes labels_one_hot = np.zeros((num_labels, num_classes)) labels_one_hot.flat[index_offset + labels_dense.ravel()] = 1 return labels_one_hot y_train01=dense_to_one_hot(y_train, num_classes=10) y_test01=dense_to_one_hot(y_test, num_classes=10) print(y_train01[:5]) print(y_test01[:5]) [[ 0. 0. 0. 0. 0. 1. 0. 0. 0. 0.] [ 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.] [ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]] [[ 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.] [ 0. 0. 1. 0. 0. 0. 0. 0. 0. 0.] [ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [ 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]] |
在one-hot编码中,只有对应类别的那个位置为1,其余都为0,我们可以使用以下代码将其转换为真实类别:
|
1 2 3 |
test=np.argmax(y_test01, axis=1) print(test[:5]) [7 2 1 0 4] |
12.5.7 数据维度
在MNIST数据集中,原始的28*28像素的黑白图片被展平为784维的向量。
|
1 2 3 4 |
print("样本维度:", X_train.shape) print("标签维度:", y_train01.shape) 样本维度: (60000, 784) 标签维度: (60000, 10) |
为使得网络结构更加清晰,在这里对这些固定维度做如下定义:
|
1 2 3 4 5 6 |
img_size = 28 # 图片的高度和宽度 img_size_flat = img_size * img_size # 展平为向量的尺寸 img_shape = (img_size, img_size) # 图片的二维尺寸 num_channels = 1 # 输入为单通道灰度图像 num_classes = 10 # 类别数目 |
12.5.8打印部分样例图片
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
def plot_images(images, cls_true, cls_pred=None): """ 绘制图像,输出真实标签与预测标签 images: 图像(9张) cls_true: 真实类别 cls_pred: 预测类别 """ assert len(images) == len(cls_true) == 9 # 保证存在9张图片 fig, axes = plt.subplots(3, 3) # 创建3x3个子图的画布 fig.subplots_adjust(hspace=0.3, wspace=0.3) # 调整每张图之间的间隔 for i, ax in enumerate(axes.flat): # 绘图,将一维向量变为二维矩阵,黑白二值图像使用 binary ax.imshow(images[i].reshape(img_shape), cmap='binary') if cls_pred is None: # 如果未传入预测类别 xlabel = "True: {0}".format(cls_true[i]) else: xlabel = "True: {0}, Pred: {1}".format(cls_true[i], cls_pred[i]) ax.set_xlabel(xlabel) # 删除坐标信息 ax.set_xticks([]) ax.set_yticks([]) plt.show() # 随机取9张图片 indices = np.arange(len(test)) np.random.shuffle(indices) indices = indices[:9] images = X_test[indices] cls_true = test[indices] plot_images(images, cls_true) |
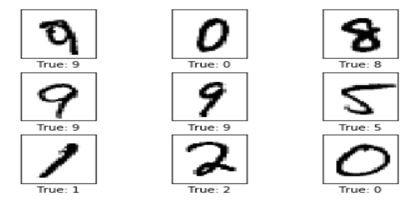
12.5.9 CNN的Tensorflow实现
TensorFlow使用计算图模型来构建神经网络。其主要流程是先建立好整个网络的计算图模型,然后再导入数据进行计算。
一个TensorFlow计算图包含以下几个部分:
Placeholder: 占位符,用来读取用户输入与输出;
Variable: 模型的变量,也称为参数,在计算过程中逐步优化;
Model: 使用的神经网络模型,也可以使用一些简单的计算;
Cost Function: 代价函数,也称损失函数,如何计算模型的误差;
Optimizer: 优化器,使用哪种优化策略来降低损失。
12.5.9.1 创建变量
卷积神经网络中有两类变量,权重和偏置项。以下为初始化这两种变量的函数,其中对权重参数采用随机生成其符合正态分布的随机值,对偏置项初始化为常量0.05。
|
1 2 3 4 5 |
def new_weights(shape): return tf.Variable(tf.truncated_normal(shape, stddev=0.05)) # 初始化为随机值 def new_biases(length): return tf.Variable(tf.constant(0.05, shape=[length])) # 初始化为常数 |
12.5.9.2 创建卷积
这个函数创建了一个卷积层。输入为4维的tensor,维度如下:
图像数量
图像高度
图像宽度
通道数
输出同样是一个4维的tensor,维度如下:
图像数量,与输入相同
图像高度,如果使用2x2 pooling,高宽都除以2
图像宽度,同上
由卷积层生成的通道数
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
def new_conv_layer(input, # 前一层. num_input_channels, # 前一层通道数 filter_size, # 卷积核尺寸 num_filters, # 卷积核数目 use_pooling=True): # 使用 2x2 max-pooling. # 卷积核权重的形状,由TensorFlow API决定 shape = [filter_size, filter_size, num_input_channels, num_filters] # 根据跟定形状创建权重 weights = new_weights(shape=shape) # 创建新的偏置,每个卷积核一个偏置 biases = new_biases(length=num_filters) # 创建卷积层。注意stride全设置为1。 # 第1个和第4个必须是1,因为第1个是图像的数目,第4个是图像的通道。 # 第2和第3指定和左右、上下的步长。 # padding设置为'SAME' 意味着给图像补零,以保证前后像素相同。 layer = tf.nn.conv2d(input=input, filter=weights, strides=[1, 1, 1, 1], padding='SAME') # 给卷积层的输出添加一个偏置,每个卷积通道一个偏置值 layer += biases # 是否使用pooling if use_pooling: # 这是 2x2 max-pooling, 表明使用 2x2 的窗口,选择每一窗口的最大值作为该窗口的像素, # 然后移动2格到下一窗口。 layer = tf.nn.max_pool(value=layer, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME') # Rectified Linear Unit (ReLU). # 对每个输入像素x,计算 max(x, 0),把负数的像素值变为0. # 这一步为原输出添加了一定的非线性特性,允许我们学习更加复杂的函数。 layer = tf.nn.relu(layer) # 注意 relu 通常在pooling前执行,但是由于 relu(max_pool(x)) == max_pool(relu(x)), # 我们可以通过先max_pooling再relu省去75%的计算。 # 返回结果层和权重,结果层用于下一层输入,权重用于显式输出 return layer, weights |
12.5.9.3 展平操作
一个卷积层的输出为4维度的tensor。我们需要在卷积层后添加一个全连接层,首先得将4为的tensor展平为2维的tensor,这样才能直接输入到全连接层。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
def flatten_layer(layer): # 获取输入层的形状, # layer_shape == [num_images, img_height, img_width, num_channels] layer_shape = layer.get_shape() # 特征数量: img_height * img_width * num_channels # 可以使用TensorFlow内建操作计算. num_features = layer_shape[1:4].num_elements() # 将形状重塑为 [num_images, num_features]. # 注意只设定了第二个维度的尺寸为num_filters,第一个维度为-1,保证第一个维度num_images不变 # 展平后的层的形状为: # [num_images, img_height * img_width * num_channels] layer_flat = tf.reshape(layer, [-1, num_features]) return layer_flat, num_features |
12.5.9.4 创建全连接层
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
def new_fc_layer(input, # 前一层. num_inputs, # 前一层输入维度 num_outputs, # 输出维度 use_relu=True): # 是否使用RELU # 新的权重和偏置,与第一章一样. weights = new_weights(shape=[num_inputs, num_outputs]) biases = new_biases(length=num_outputs) # 计算 y = wx + b,同第一章 layer = tf.matmul(input, weights) + biases # 是否使用RELU if use_relu: layer = tf.nn.relu(layer) return layer |
12.5.9.5 定义占位符
占位符(Placeholder)为输入与输出占据位置,这些输入输出一般在不同的轮次都会有所变化。由于TensorFlow先构图再计算,所以需要使用占位符为输入和输出预留位置。
|
1 2 3 4 |
x = tf.placeholder(tf.float32, shape=[None, img_size_flat], name='x') # 原始输入 x_image = tf.reshape(x, [-1, img_size, img_size, num_channels]) # 转换为2维图像 y_true = tf.placeholder(tf.float32, shape=[None, num_classes], name='y_true') # 原始输出 y_true_cls = tf.argmax(y_true, axis=1) # 转换为真实类别,与之前的使用placeholder不同 |
12.5.9.6 定义卷积层1
|
1 2 3 4 5 6 7 8 |
layer_conv1, weights_conv1 = \ new_conv_layer(input=x_image, # 输入图像 num_input_channels=num_channels, # 输入通道数 filter_size=filter_size1, # 卷积核尺寸 num_filters=num_filters1, # 卷积核数目 use_pooling=True) print(layer_conv1) Tensor("Relu:0", shape=(?, 14, 14, 16), dtype=float32) |
输入为(?, 28, 28, 1)的图像,其中?为图像数量。可以看到,第一个卷积层的输入为(?, 14, 14, 16)的tensor,即14x14像素的16通道图像。
12.5.9.7 定义卷积层2
|
1 2 3 4 5 6 7 8 |
layer_conv2, weights_conv2 = \ new_conv_layer(input=layer_conv1, num_input_channels=num_filters1, filter_size=filter_size2, num_filters=num_filters2, use_pooling=True) print(layer_conv2) Tensor("Relu_1:0", shape=(?, 7, 7, 36), dtype=float32) |
12.5.9.8 定义展平层
展平层将第二个卷积层展平为二维tensor。
|
1 2 3 |
layer_flat, num_features = flatten_layer(layer_conv2) print(layer_flat) Tensor("Reshape_1:0", shape=(?, 1764), dtype=float32) |
12.5.9.9 定义全连接层1
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
layer_fc1 = new_fc_layer(input=layer_flat, # 展平层输出 num_inputs=num_features, # 输入特征维度 num_outputs=fc_size, # 输出特征维度 use_relu=True) print(layer_fc1) Tensor("Relu_2:0", shape=(?, 128), dtype=float32) <h3>12.5.9.9 定义全连接层2</h3> layer_fc2 = new_fc_layer(input=layer_fc1, # 上一全连接层 num_inputs=fc_size, # 输入特征维度 num_outputs=num_classes, # 输出类别数 use_relu=False) print(layer_fc2) Tensor("add_4:0", shape=(?, 10), dtype=float32) |
输出为(?, 10)的二维tensor,意在判定输入图像属于哪一类, 注意该层未使用relu,因为将要输入到后续的softmax中。
12.5.9.10 预测类别
第二个全连接层估计输入的图像属于某一类别的程度,这个估计有些粗糙,需要添加一个softmax层归一化为概率表示。
|
1 2 3 4 5 6 7 8 |
y_pred = tf.nn.softmax(layer_fc2) # softmax归一化 y_pred_cls = tf.argmax(y_pred, axis=1) # 真实类别 [/cceN_python] <h3>12.5.9.11 定义代价函数</h3> 这里以交叉熵为代价函数或损失函数。 <pre class="lang:default decode:true " > cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=layer_fc2,labels=y_true) cost = tf.reduce_mean(cross_entropy) |
12.5.9.12 选择优化方法
使用自适应的梯度下降优化法,Adam。
|
1 |
optimizer = tf.train.AdamOptimizer(learning_rate=1e-4).minimize(cost) |
12.5.9.13 模型性能度量
|
1 2 3 4 5 6 7 8 9 |
correct_prediction = tf.equal(y_pred_cls, y_true_cls) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) [/cceN_python] <h3>12.5.10运行TensorFlow计算图</h3> <h3>12.5.10.1创建Session以及变量初始化</h3> TensorFlow计算图运行在一个session中,计算之前需要先创建这个session,并初始化其中的一些变量(w 和 b),TensorFlow使用session.run()来运行计算图。 <pre class="lang:default decode:true " > session = tf.Session() # 创建session session.run(tf.global_variables_initializer()) # 变量初始化 |
12.5.10.2执行优化的帮助函数
定义批处理函数,该函数在优化算法中被调用。
|
1 2 3 4 5 6 7 8 9 10 11 |
def next_batch(num, data, labels): ''' Return a total of `num` random samples and labels. ''' idx = np.arange(0 , len(data)) np.random.shuffle(idx) idx = idx[:num] data_shuffle = [data[ i] for i in idx] labels_shuffle = [labels[ i] for i in idx] return np.asarray(data_shuffle), np.asarray(labels_shuffle) |
定义优化算法,调用批处理函数、Adam优化器等,并增加部分状态输出的代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
train_batch_size = 64 # 计算目前执行的总迭代次数 total_iterations = 0 def optimize(num_iterations): # 保证更新全局变量. global total_iterations # 用来输出用时. start_time = time.time() for i in range(total_iterations, total_iterations + num_iterations): # 获取一批数据,放入dict #x_batch, y_true_batch = data.train.next_batch(train_batch_size) x_batch, y_true_batch = next_batch(train_batch_size, X_train, y_train01) #x_batch = X_train.next_batch(train_batch_size) #y_true_batch = y_test01.next_batch(train_batch_size) feed_dict_train = {x: x_batch, y_true: y_true_batch} # 运行优化器 session.run(optimizer, feed_dict=feed_dict_train) # 每100轮迭代输出状态 if i % 100 == 0: # 计算训练集准确率. acc = session.run(accuracy, feed_dict=feed_dict_train) msg = "迭代轮次: {0:>6}, 训练准确率: {1:>6.1%}" print(msg.format(i + 1, acc)) total_iterations += num_iterations end_time = time.time() time_dif = end_time - start_time # 输出用时. print("用时: " + str(timedelta(seconds=int(round(time_dif))))) |
12.5.10.3执行优化的帮助函数
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
def plot_example_errors(cls_pred, correct): # 计算错误情况 incorrect = (correct == False) images = X_test[incorrect] cls_pred = cls_pred[incorrect] cls_true = test[incorrect] # 随机挑选9个 indices = np.arange(len(images)) np.random.shuffle(indices) indices = indices[:9] plot_images(images[indices], cls_true[indices], cls_pred[indices]) def plot_confusion_matrix(cls_pred): cls_true = test # 真实类别 # 使用scikit-learn的confusion_matrix来计算混淆矩阵 cm = confusion_matrix(y_true=cls_true, y_pred=cls_pred) # 打印混淆矩阵 print(cm) # 将混淆矩阵输出为图像 plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues) # 调整图像 plt.tight_layout() plt.colorbar() tick_marks = np.arange(num_classes) plt.xticks(tick_marks, range(num_classes)) plt.yticks(tick_marks, range(num_classes)) plt.xlabel('Predicted') plt.ylabel('True') plt.show() |
12.5.10.4显示性能的帮助函数
用来输出测试准确率的的函数。计算所有图像的分类需要一定的时间,因此我们在上面定义的一些函数中重用了分类结果。这个函数会占据大量的内存,所以将测试集分成了多个小的批次。如果你的机器内存太小,你可以尝试减小batch_size。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
# 将测试集分成更小的批次 test_batch_size = 256 def print_test_accuracy(show_example_errors=False, show_confusion_matrix=False): # 测试集图像数量. num_test = len(X_test) # 为预测结果申请一个数组. cls_pred = np.zeros(shape=num_test, dtype=np.int) # 数据集的起始id为0 i = 0 while i < num_test: # j为下一批次的截止id j = min(i + test_batch_size, num_test) # 获取i,j之间的图像 images = X_test[i:j, :] # 获取相应标签. labels = y_test01[i:j, :] # 创建feed_dict feed_dict = {x: images, y_true: labels} # 计算预测结果 cls_pred[i:j] = session.run(y_pred_cls, feed_dict=feed_dict) # 设定为下一批次起始值. i = j cls_true = test # 正确的分类 correct = (cls_true == cls_pred) # 正确分类的数量 correct_sum = correct.sum() # 分类准确率 acc = float(correct_sum) / num_test # 打印准确率. msg = "测试集准确率: {0:.1%} ({1} / {2})" print(msg.format(acc, correct_sum, num_test)) # 打印部分错误样例. if show_example_errors: print("Example errors:") plot_example_errors(cls_pred=cls_pred, correct=correct) # 打印混淆矩阵. if show_confusion_matrix: print("Confusion Matrix:") plot_confusion_matrix(cls_pred=cls_pred) [/cceN_python] <h3>12.5.10.4优化前的性能测试</h3> [cceN_python theme="blackboard"] print_test_accuracy() 测试集准确率: 10.2% (1022 / 10000) |
可以看到,测试的准确率极低,但是函数的功能正常。
12.5.10.5执行一轮优化后的性能
|
1 2 3 4 5 6 7 8 9 10 |
optimize(num_iterations=1) print_test_accuracy() [/cceN_python] 迭代轮次: 1, 训练准确率: 12.5% 用时: 0:00:00 测试集准确率: 10.8% (1076 / 10000) <h3>12.5.10.6 100轮优化后的性能</h3> <pre class="lang:default decode:true " > optimize(num_iterations=99) print_test_accuracy() |
用时: 0:00:14
测试集准确率: 80.1% (8010 / 10000)
可以看到,执行100轮迭代后,性能存在大幅度提升。
12.5.10.7 1000轮优化后的性能
|
1 2 |
optimize(num_iterations=900) print_test_accuracy(show_example_errors=True) |
迭代轮次: 101, 训练准确率: 76.6%
迭代轮次: 201, 训练准确率: 76.6%
迭代轮次: 301, 训练准确率: 93.8%
迭代轮次: 401, 训练准确率: 87.5%
迭代轮次: 501, 训练准确率: 90.6%
迭代轮次: 601, 训练准确率: 96.9%
迭代轮次: 701, 训练准确率: 93.8%
迭代轮次: 801, 训练准确率: 98.4%
迭代轮次: 901, 训练准确率: 96.9%
用时: 0:02:07
测试集准确率: 95.6% (9563 / 10000)
Example errors:
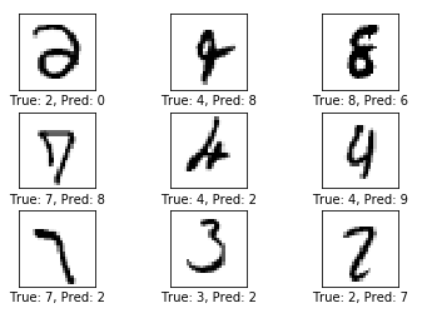
可以发现,测试集的准确率为95.6%,已经比传统的90.9%要高。输出的部分错误样例显示,部分形状相似的数字仍然难以区分。
12.5.10.8 10000轮优化后的性能
|
1 2 3 |
optimize(num_iterations=9000) print_test_accuracy(show_example_errors=True, show_confusion_matrix=True) |
迭代轮次: 8701, 训练准确率: 100.0%
迭代轮次: 8801, 训练准确率: 100.0%
迭代轮次: 8901, 训练准确率: 100.0%
迭代轮次: 9001, 训练准确率: 100.0%
迭代轮次: 9101, 训练准确率: 98.4%
迭代轮次: 9201, 训练准确率: 100.0%
迭代轮次: 9301, 训练准确率: 95.3%
迭代轮次: 9401, 训练准确率: 100.0%
迭代轮次: 9501, 训练准确率: 100.0%
迭代轮次: 9601, 训练准确率: 100.0%
迭代轮次: 9701, 训练准确率: 100.0%
迭代轮次: 9801, 训练准确率: 100.0%
迭代轮次: 9901, 训练准确率: 100.0%
用时: 0:21:04
测试集准确率: 98.3% (9833 / 10000)
Example errors:

Confusion Matrix:
[[ 977 0 2 0 0 0 0 1 0 0]
[ 0 1129 5 0 0 0 0 1 0 0]
[ 0 1 1028 0 1 0 0 2 0 0]
[ 0 0 4 996 0 9 0 0 0 1]
[ 0 1 2 0 973 0 0 0 0 6]
[ 1 0 0 4 0 886 1 0 0 0]
[ 6 2 2 1 3 8 935 0 1 0]
[ 1 2 14 2 0 0 0 1002 2 5]
[ 12 0 17 5 5 9 1 2 914 9]
[ 2 0 2 2 3 6 0 1 0 993]]
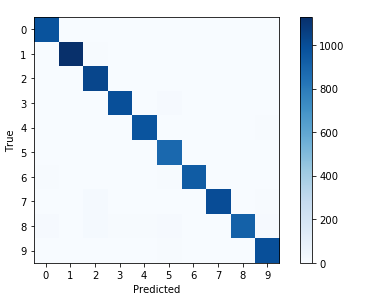
经过10000轮迭代后,测试集的准确率达到了98.3%的准确率。在分错的样本中,部分用肉眼也难以分辨。而混淆矩阵表明绝大部分的样本都分类正确。这是一个非常好的模型。
12.5.11权重和层的可视化
为了更好的理解卷积神经网络为何能识别手写体数字,我来来可视化部分权重和层输出。
12.5.11.1卷积权重可视化
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
def plot_conv_weights(weights, input_channel=0): # weights_conv1 or weights_conv2. # 运行weights以获得权重 w = session.run(weights) # 获取权重最小值最大值,这将用户纠正整个图像的颜色密集度,来进行对比 w_min = np.min(w) w_max = np.max(w) # 卷积核树木 num_filters = w.shape[3] # 需要输出的卷积核 num_grids = math.ceil(math.sqrt(num_filters)) fig, axes = plt.subplots(num_grids, num_grids) for i, ax in enumerate(axes.flat): # 只输出有用的子图. if i<num_filters: # 获得第i个卷积核在特定输入通道上的权重 img = w[:, :, input_channel, i] ax.imshow(img, vmin=w_min, vmax=w_max, interpolation='nearest', cmap='seismic') # 移除坐标. ax.set_xticks([]) ax.set_yticks([]) plt.show() |
12.5.11.2卷积层输出可视化
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
def plot_conv_layer(layer, image): # layer_conv1 or layer_conv2. # feed_dict只需要x,标签信息在此不需要. feed_dict = {x: [image]} # 获取该层的输出结果 values = session.run(layer, feed_dict=feed_dict) # 卷积核树木 num_filters = values.shape[3] # 每行需要输出的卷积核网格数 num_grids = math.ceil(math.sqrt(num_filters)) fig, axes = plt.subplots(num_grids, num_grids) for i, ax in enumerate(axes.flat): # 只输出有用的子图. if i<num_filters: # 获取第i个卷积核的输出 img = values[0, :, :, i] ax.imshow(img, interpolation='nearest', cmap='binary') # 移除坐标. ax.set_xticks([]) ax.set_yticks([]) plt.show() |
12.5.11.3打印输入图像
|
1 2 3 4 5 6 7 8 9 |
def plot_image(image): plt.imshow(image.reshape(img_shape), interpolation='nearest', cmap='binary') plt.show() image1 = X_test[0] plot_image(image1) |

12.5.11.4显示卷积层1的权重
|
1 |
plot_conv_weights(weights=weights_conv1) |
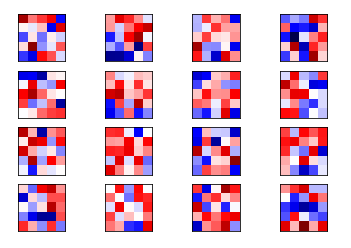
以上就是16个卷积核在第一个通道的权重情况。其中红色为正的权重,蓝色为负的权重。在这里我们很难判别这些权重是如何起作用的。
将image1输入卷积层1,得到使用不同卷积后得到的图像,这些图像的棱角更加分明,而且在不同的边的突出情况也不同:
|
1 |
plot_conv_layer(layer=layer_conv1, image=image1) |

将image2输入卷积层1,得到如下图像,在不同部位的突出情况不同
|
1 2 |
image2 = X_test[3] plot_conv_layer(layer=layer_conv1, image=image2) |

12.5.11.5显示卷积层2的权重
现在输出第二个卷积层的权重。
由于卷积层1有16个输出通道,这意味着卷积层2有16个输入通道,每个通道的输入又对应36个输出通道,因此总共有16x36个通道的卷积核。我们先输出第一个通道的卷积核
|
1 |
plot_conv_weights(weights=weights_conv2, input_channel=0) |

这些权重相对与卷积层1的权重更加抽象,无法用语言来解释。接下来输出第二个通道的卷积核。
|
1 |
plot_conv_weights(weights=weights_conv2, input_channel=1) |

可以说明,不同输入通道对应的卷积核是不同的。将image1在卷积层1的输出再次输入卷积层2,得到如下输出:
[cceN_python theme="blackboard"]
plot_conv_layer(layer=layer_conv1, image=image2)

所输出的图像达到了一个更高的层次,卷积核试图提取一些边缘化的特征,这些特征对于同类图像的变化并不敏感。
在运行完整个计算图后,需要将它关闭,否则将一直占用资源:
|
1 |
session.close() |
参考:https://gaussic.github.io/2017/08/14/tensorflow-cnn/
潜心学习,认真拜读!
Pingback引用通告: Python与人工智能 – 飞谷云人工智能