第10章 K-means聚类算法及实例
10.1 K-means简介
机器学习中有两类的大问题，一个是分类，一个是聚类。
分类是根据一些给定的已知类别标识的样本，训练某种学习机器，使它能够对未知类别的样本进行分类。这属于监督学习。而聚类指事先并不知道任何样本的类别标识，希望通过某种算法来把一组未知类别的样本划分成若干类别，这在机器学习中被称作无监督学习。在本章，我们关注其中一个比较简单的聚类算法：k-means算法。
10.2 K-means 算法
k-means算法是一种很常见的聚类算法，它的基本思想是：
(1)适当选择k个类的初始中心
(2)在第i次迭代中，对任意一个样本，求其到K个中心的距离，将该样本归到距离 最短的中心所在的类
(3)利用均值等方法更新该类的中心值
(4)对于所有的K个聚类中心，如果利用（2）（3）的迭代法更新后，值保持不变， 则迭代结束，否则继续迭代。
最后结果是同一类簇中的对象相似度极高，不同类簇中的数据相似度极低。
10.3 K-means简单实例
假定我们有如下9个点：
A1(2, 10) A2(2, 5) A3(8, 4) A4(5, 8) A5(7, 5) A6(6, 4) A7(1, 2) A8(4, 9)
现希望分成3个聚类（即k=3）
初始化选择 A1(2, 10), A4(5, 8) ，A7(1, 2)为聚类中心点，假设两点距离定义为ρ(a, b) = |x2 – x1| + |y2 – y1| . （当然也可以定义为其它格式，如欧氏距离）
第一步：选择3个聚类中，分别为A1，A4，A7
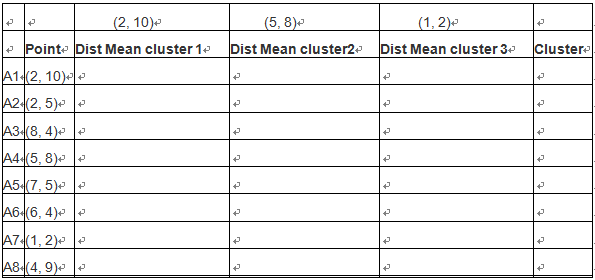
这些点的分布图如下：
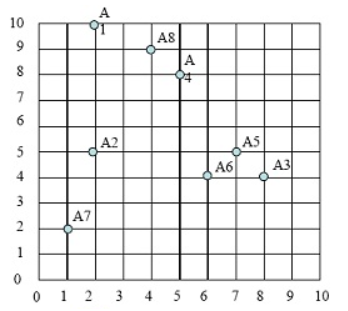
第二步：计算各点到3个类中心的距离，那个点里类中心最近，就把这个样本点
划归到这个类。选定3个类中心（即:A1，A4，A7），如下图：
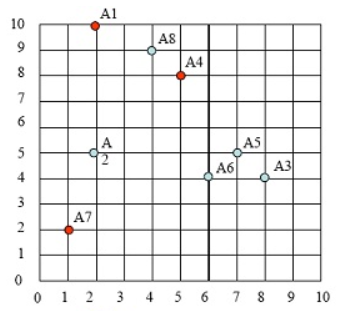
对A1点，计算其到每个cluster 的距离
A1->class1 = |2-2|+|10-10}=0
A1->class2 = |2-5|+|10-8|=5
A1->class3 = |2-1|+|10-2|=9
因此A1 属于cluster1，如下图：
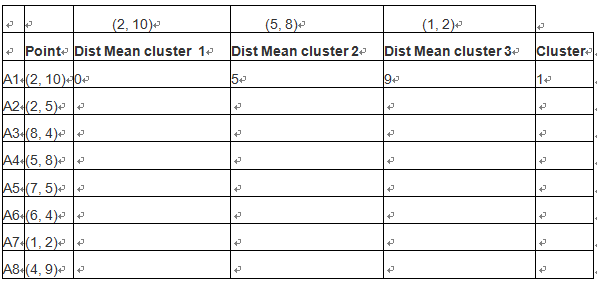
按照类似方法，算出各点到聚类中心的距离，然后按照最近原则，把样本点放在那个族中。如下表格：
根据距离最短原则，样本点的第一次样本划分，如下图：
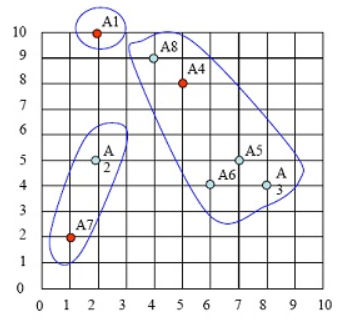
第三步：求出各类中样本点的均值，并以此为类的中心。
cluster1只有1个点，因此A1为中心点
cluster2的中心点为 ( (8+5+7+6+4)/5,(4+8+5+4+9)/5 )=（6,6）。注意：这个点并非样本点。
cluster3的中心点为( (2+1)/2, (5+2)/2 )= (1.5, 3.5)，
新族的具体请看下图中x点：
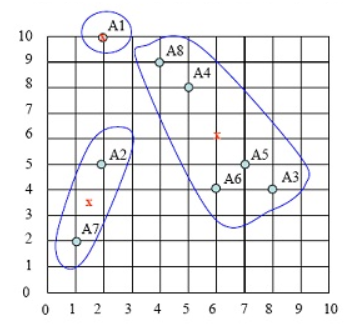
第四步：计算各样本点到各聚类中心的距离，重复以上第二、第三步，把样本划分到新聚类中，如下图：
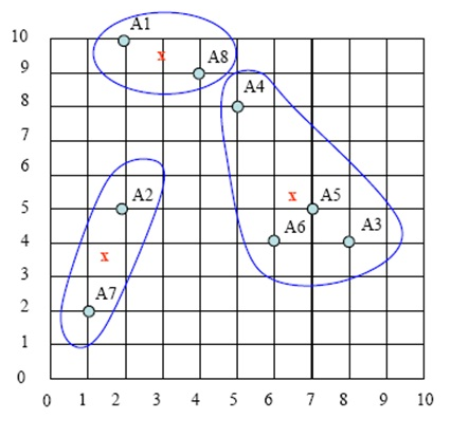持续迭代，直到前后两次迭代不发生变化为止，如下：
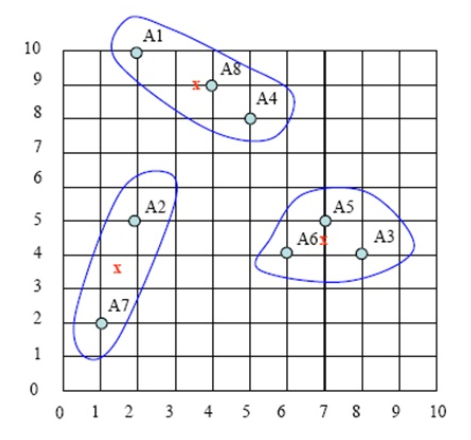
10.4 sklearn.K-means的实例
初始化聚类中心比较有讲究，上面这个实例我们是人工指定，A1、A4、A7为初始化的聚类中心；如果K值选择不当或聚类中心选择不当，则可能导致聚类效果不佳。因此，在实际项目中往往采用随机选择K个聚类中心，另外，K的选取也是很重要的，K的选取我们也有比较好的方法,如肘（elbow）方法、轮廓图（silhouette plot）方法等，这里就不展开来说，有兴趣的读者可以查阅相关资料。
import numpy as np #科学计算包
import matplotlib.pyplot as plt #python画图包
from sklearn.cluster import KMeans #导入K-means算法包
from sklearn.datasets import make_blobs
import matplotlib.font_manager as fm ###便于中文显示
myfont = fm.FontProperties(fname='/home/hadoop/anaconda3/lib/python3.6/site-packages/matplotlib/mpl-data/fonts/ttf/simhei.ttf')
plt.figure(figsize=(12, 12))
'''''
make_blobs函数是为聚类产生数据集
产生一个数据集和相应的标签
n_samples:表示数据样本点个数,默认值100
n_features:表示数据的维度，默认值是2
centers:产生数据的聚类中心点，默认值3
init:采用随机还是k-means++等（可使聚类中心尽可能的远的一种方法）
cluster_std：数据集的标准差，浮点数或者浮点数序列，默认值1.0
center_box：中心确定之后的数据边界，默认值(-10.0, 10.0)
shuffle ：洗乱，默认值是True
random_state:随机生成器的种子
'''
n_samples = 1500
random_state = 10
X, y = make_blobs(n_samples=n_samples, random_state=random_state)
# Incorrect number of clusters
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X)
plt.subplot(221) #在2图里添加子图1
plt.scatter(X[:, 0], X[:, 1], c=y_pred) #scatter绘制散点
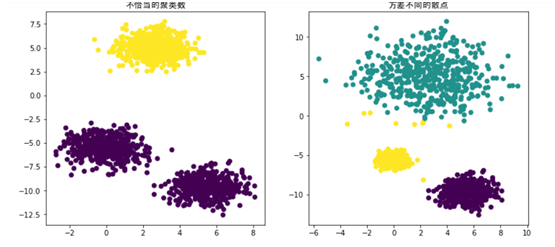
plt.title("不恰当的聚类数",fontproperties=myfont,size=12) #加标题
# Different variance
X_varied, y_varied = make_blobs(n_samples=n_samples,
cluster_std=[1.0, 2.5, 0.5],
random_state=random_state)
y_pred = KMeans(n_clusters=3, init='random',random_state=random_state).fit_predict(X_varied)
plt.subplot(222)#在2图里添加子图3
plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("方差不同的散点",fontproperties=myfont,size=12)
plt.show()
10.5 Mini Batch K-Means算法
对K-means算法，如果原数据很多，其计算量非常大，对于大数据是否有更好的方法呢？在计算梯度时，我们用整个数据集计算，如果数据量大的话，我们可以采用随机梯度的方法。同理，我们在处理聚类算法时，也有类似的方法，这就是scikit-learn提供的Mini Batch K-Means算法，其具体方法如下：
Mini Batch K-Means算法是K-Means算法的变种，采用小批量的数据子集减小计算时间，同时仍试图优化目标函数，这里所谓的小批量是指每次训练算法时所随机抽取的数据子集，采用这些随机产生的子集进行训练算法，大大减小了计算时间，与其他算法相比，减少了k-均值的收敛时间，小批量k-均值产生的结果，一般只略差于标准算法。
该算法的迭代步骤有两步：
1：从数据集中随机抽取一些数据形成小批量，把他们分配给最近的质心
2：更新质心
与K均值算法相比，数据的更新是在每一个小的样本集上。对于每一个小批量，通过计算平均值得到更新质心，并把小批量里的数据分配给该质心，随着迭代次数的增加，这些质心的变化是逐渐减小的，直到质心稳定或者达到指定的迭代次数，停止计算
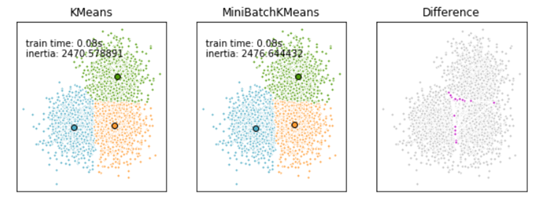
Mini Batch K-Means比K-Means有更快的 收敛速度，但同时也降低了聚类的效果，但是在实际项目中却表现得不明显，这是一张k-means和mini batch k-means的实际效果对比图。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import MiniBatchKMeans, KMeans
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.datasets.samples_generator import make_blobs
##############################################################################
# Generate sample data
np.random.seed(0)
batch_size = 45
centers = [[1, 1], [-1, -1], [1, -1]] #初始化三个中心
n_clusters = len(centers) #聚类的数目为3
#产生3000组两维的数据，以上边三个点为中心，以（-10,10）为边界，数据集的标准差是0.7
X, labels_true = make_blobs(n_samples=3000, centers=centers, cluster_std=0.7)
##############################################################################
# Compute clustering with Means
k_means = KMeans(init='k-means++', n_clusters=3, n_init=10)
t0 = time.time() #当前时间
k_means.fit(X)
#使用K-Means 对 3000数据集训练算法的时间消耗
t_batch = time.time() - t0
##############################################################################
# Compute clustering with MiniBatchKMeans
mbk = MiniBatchKMeans(init='k-means++', n_clusters=3, batch_size=batch_size,
n_init=10, max_no_improvement=10, verbose=0)
t0 = time.time()
mbk.fit(X)
#使用MiniBatchKMeans 对 3000数据集训练算法的时间消耗
t_mini_batch = time.time() - t0
##############################################################################
# Plot result
#创建一个绘图对象, 并设置对象的宽度和高度, 如果不创建直接调用plot, Matplotlib会直接创建一个绘图对象
'''''
当绘图对象中有多个轴的时候，可以通过工具栏中的Configure Subplots按钮，
交互式地调节轴之间的间距和轴与边框之间的距离。
如果希望在程序中调节的话，可以调用subplots_adjust函数，
它有left, right, bottom, top, wspace, hspace等几个关键字参数，
这些参数的值都是0到1之间的小数，它们是以绘图区域的宽高为1进行正规化之后的坐标或者长度。
'''
fig = plt.figure(figsize=(8, 3))
fig.subplots_adjust(left=0.02, right=0.98, bottom=0.05, top=0.9)
colors = ['#4EACC5', '#FF9C34', '#4E9A06']
# We want to have the same colors for the same cluster from the
# MiniBatchKMeans and the KMeans algorithm. Let's pair the cluster centers per
# closest one.
k_means_cluster_centers = np.sort(k_means.cluster_centers_, axis=0)
mbk_means_cluster_centers = np.sort(mbk.cluster_centers_, axis=0)
k_means_labels = pairwise_distances_argmin(X, k_means_cluster_centers)
mbk_means_labels = pairwise_distances_argmin(X, mbk_means_cluster_centers)
order = pairwise_distances_argmin(k_means_cluster_centers,
mbk_means_cluster_centers)
# KMeans
ax = fig.add_subplot(1, 3, 1) #add_subplot 图像分给为 一行三列，第一块
for k, col in zip(range(n_clusters), colors):
my_members = k_means_labels == k
cluster_center = k_means_cluster_centers[k]
ax.plot(X[my_members, 0], X[my_members, 1], 'w',
markerfacecolor=col, marker='.')
ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=6)
ax.set_title('KMeans')
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, 'train time: %.2fs\ninertia: %f' % (
t_batch, k_means.inertia_))
# MiniBatchKMeans
ax = fig.add_subplot(1, 3, 2)#add_subplot 图像分给为 一行三列，第二块
for k, col in zip(range(n_clusters), colors):
my_members = mbk_means_labels == order[k]
cluster_center = mbk_means_cluster_centers[order[k]]
ax.plot(X[my_members, 0], X[my_members, 1], 'w',
markerfacecolor=col, marker='.')
ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=6)
ax.set_title('MiniBatchKMeans')
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, 'train time: %.2fs\ninertia: %f' %
(t_mini_batch, mbk.inertia_))
# Initialise the different array to all False
different = (mbk_means_labels == 4)
ax = fig.add_subplot(1, 3, 3)#add_subplot 图像分给为 一行三列，第三块
for k in range(n_clusters):
different += ((k_means_labels == k) != (mbk_means_labels == order[k]))
identic = np.logical_not(different)
ax.plot(X[identic, 0], X[identic, 1], 'w',
markerfacecolor='#bbbbbb', marker='.')
ax.plot(X[different, 0], X[different, 1], 'w',
markerfacecolor='m', marker='.')
ax.set_title('Difference')
ax.set_xticks(())
ax.set_yticks(())
plt.show()
参考网站：http://blog.csdn.net/gamer_gyt/article/details/51244850
不止一次的来，不止一次的去，来来去去，这就是这个博客的魅力！
Pingback引用通告： Python与人工智能 – 飞谷云人工智能