第11章 神奇的SVM及实例分析
11.1 SVM简介
支持向量机(SupportVector Machines),在处理线性数据集、非线性数据集都有较好效果,在机器学习或者模式识别领域可是无人不知,无人不晓。八九十年代的时候,和神经网络一决雌雄,独领风骚几十年,甚至有人把神经网络八九年代的再度沉寂归功于它。
它的强大或神奇与它采用的相关技术不无关系,如最大类间隔、松弛变量、核函数等等(这些技术本章都会介绍),使用这些技术使其在众多机器学习方法中脱颖而出。虽然几十年过去了,但风采依旧,究其原因:与其高效、简洁、易用的特点分不开,其中一些处理思想与当今深度学习技术有很大关系,如其用核方法解决非线性数据集分类问题,很像带隐含层的神经网络,可以说两者有同工异曲之妙。
分类的方法有很多,如线性回归、逻辑回归、决策树、贝叶斯等等,分类的目的是学会一个分类函数或分类模型(或者叫做分类器),该模型能把数据集中的数据项映射到给定类别中的某一个,对新数据通过这个映射,预测其类别。
支持向量机进行分类,目的也是一样:得到一个分类器或分类模型,不过它的分类器一个超平面(如果数据集是二维,这个超平面就是直线,三维数据集,就是平面,以此类推),这个超平面把样本一分为二,当然,这种划分不是简单划分,需要使正例和反例之间的间隔最大。间隔最大,其泛化能力就最强。如何得到这样一个超平面?下级我们通过用一个二维空间例子来说明。
11.2 分类间隔最大的超平面
何为超平面?哪种超平面是我们需要?,我们首先看下图的几个超平面或直线。

如何获取最大化分类间隔?分类算法优化目标通常是最小化分类误差,但对SVM而言,我们的优化的目标是最大化分类间隔。所谓间隔是指两个分离的超平面间的距离,其中最靠近超平面的训练样本又称为支持向量(support vector)。以下我们通过一个二维空间的简单实例来进一步说明。
假设在一个二维空间,分布下例这些点(有些是圆点,有些是方块)。



所以我们的问题就变成:

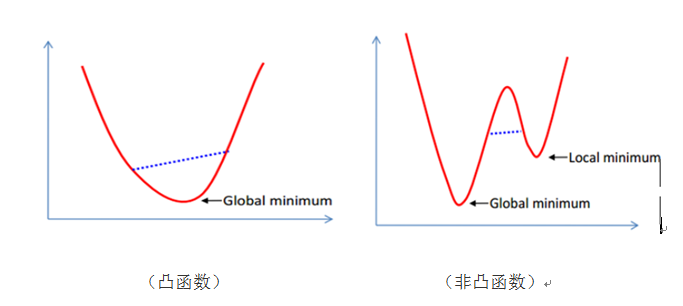
这是个凸二次规划问题。什么叫凸?凸集是指这样一些点的集合,其中任取两个点连一条直线,这条线上的点仍然在这个集合内部,因此说“凸”。例如下图,对于凸函数(在数学表示上,满足约束条件是仿射函数,也就是线性的Ax+b的形式)来说,局部最优就是全局最优,但对非凸函数来说就不是了。二次表示目标函数是自变量的二次函数。
既然是凸二次规划问题,就可以通过一些现成的 QP (Quadratic Programming) 的优化工具来得到最优解。所以,我们的问题到此为止就算全部解决了。虽然这个问题确实是一个标准的 QP 问题,但是它也有它的特殊结构,通过 Lagrange Duality 变换到对偶变量 (dual variable) 的优化问题之后,可以找到一种更加有效的方法来进行求解,而且通常情况下这种方法比直接使用通用的 QP 优化包进行优化要高效得多。也就说,除了用解决QP问题的常规方法之外,还可以应用拉格朗日对偶性,通过求解对偶问题得到最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:一是对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。至于对偶问题及其优化这里就不展开来说了,有兴趣的读者可以参考有关资料。
11.3使用松弛向量解决非线性可分问题
实际数据集往往很难找到一条直线或一个超平面就可一分为二,或者这些数据集是线性可分的。如果出现非线性数据集,我们该如何处理呢?这里我们介绍一种所谓软间隔的分类方法,这种方法由Vladimir Vapnik在1995年引入,其基本思想是引入一个松弛系数ξ,放松线性约束的条件,以便在适当的罚项成本下,对错误分类的情况优化时也能收敛。
为了处理这种情况,我们允许数据点在一定程度上偏离超平面。也就是允许一些点跑到H1和H2之间,也就是他们到分类面的间隔会小于1。如下图:
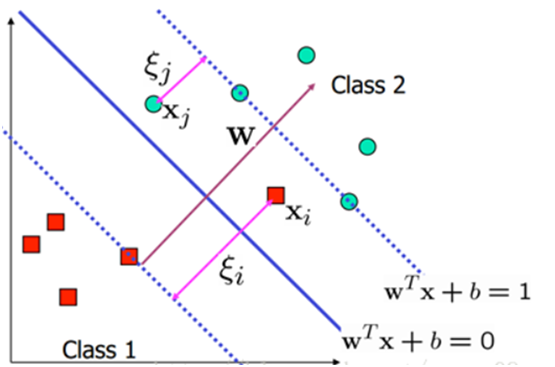

其中C是离群点的权重,引入非负参数ξi后(称为松弛变量),就允许某些样本点的函数间隔小于1,即在最大间隔区间里面,或者函数间隔是负数,即样本点在对方的区域中。而放松限制条件后,我们需要重新调整目标函数,以对离群点进行处罚,目标函数后面加上的第二项就表示离群点越多,目标函数值越大,而我们要求的是尽可能小的目标函数值。通过变量C我们可以控制对错误分类的惩罚程度。C越大表明离群点对目标函数影响越大,也就是越不希望看到离群点。这时候,间隔也会很小。我们看到,目标函数控制了离群点的数目和程度,使大部分样本点仍然遵守限制条件,如下图所示:

至此,我们已经了解了线性SVM的基本概念,主要原理,接下来我们通过一个实例来演示一个SVM模型对鸢尾花数据集中的样本进行分类。
11.4 SVM分类实例
接下来我们以鸢尾花卉数据集(lris)样本,使用SVM对其进行分类,lris是一类多重变量分析的数据集。通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类。
1)导入数据
使用sklearn中导入数据的库(datasets)进行数据的导入,为方便可视化起见,这里我们花瓣长度,花瓣宽度为两个特征,并由此构建一个特征矩阵X,同时将对应花的类标赋给向量Y,具体实现如下:
import numpy as np
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
2)对数据进行标准化处理
sc = StandardScaler()
sc.fit(X)
X_std = sc.transform(X)
4)为更好的显示划分后的效果,这里我们先定义几个函数,用来图形化数据。
import matplotlib.pyplot as plt
import warnings
def versiontuple(v):
return tuple(map(int, (v.split("."))))
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=cmap(idx),
marker=markers[idx], label=cl)
5)利用SVM对对数据集进行分类,这里使用了松弛变量来处理非线性数据集。
from sklearn.svm import SVC
import matplotlib.font_manager as fm ###便于中文显示
myfont = fm.FontProperties(fname='/home/hadoop/anaconda3/lib/python3.6/site-packages/matplotlib/mpl-data/fonts/ttf/simhei.ttf')
svm = SVC(kernel='linear', C=1.0, random_state=0)
svm.fit(X_std, y)
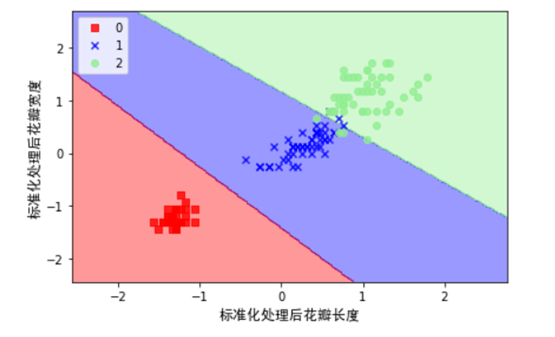
plot_decision_regions(X_std, y,classifier=svm)
plt.xlabel("标准化处理后花瓣长度",fontproperties=myfont,size=12)
plt.ylabel("标准化处理后花瓣宽度",fontproperties=myfont,size=12)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
11.5在 SVM中应用核函数
上节我们介绍了使用松弛变量处理非线性数据集(含有一些离群点)问题,效果还不错。但有些数据集其分布就是非线性可分的,如比较典型的“异或”问题,遇到这种数据集,我们该如何处理呢?显然使用松弛变量难以达到满意效果,不过没有关系,此时,我们可以使用SVM的一种强大而神奇的核函数法。通过核函数我们可以把线性不可分数据集转换为线性可分(在更高维度空间中)。
接下来我们简单介绍一下核函数或核方法。
我们先通过一个图及一个简单实例,先来大致了解一下SVM的核威力。我们先一个图,给大家一点感性认识:
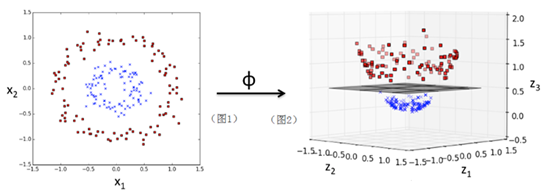
图1是一个二维空间上的一些散点分布图,通过一个核函数ϕ:
ϕ(x1,x2)=(z1,z2,z3)=(x1,x2,〖x1〗^2+〖x2〗^2)
把一个在二维空间线性不可分的数据集映射到三维空间(图2)后,就可以线性可分了(其中超平面可以把数据分成上下两部分)。
这是核方法的一个直观认识,下面我们使用scikit-learn包的SVM类,具体实现一个核方法。
1)在二维空间,生成一个类似‘异或’的数据集
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(0)
X_xor = np.random.randn(200, 2)
y_xor = np.logical_xor(X_xor[:, 0] > 0,
X_xor[:, 1] > 0)
y_xor = np.where(y_xor, 1, -1)
plt.scatter(X_xor[y_xor == 1, 0],
X_xor[y_xor == 1, 1],
c='b', marker='x',
label='1')
plt.scatter(X_xor[y_xor == -1, 0],
X_xor[y_xor == -1, 1],
c='r',
marker='s',
label='-1')
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.legend(loc='best')
plt.tight_layout()
plt.show()
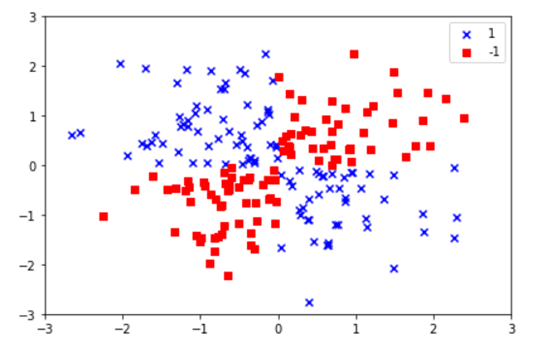
显然,对这个数据集是线性不可分的,即无法找到一条直线或超平面,把这个数据集划分为两类。
接下来我们采用SVM类中一个高斯核或径向基函数核(Radial Basis Function Kernel,RBF Kernel ),把数据映射到一个高维空间,然后利用SVM对其进行分类或划分。
svm.fit(X_xor, y_xor)
plot_decision_regions(X_xor, y_xor,
classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()

从以上图可以看到,SVM比较完美的把不同类型的点划分成了两部分。
核函数我们可以把它理解为把低维数据集映射为高维数据集的映射或相似函数。接下来我们看一下核函数一般形式及特点、常用核函数。
设xi,xj∈X,X属于R(n)空间,非线性函数Φ实现输入空间X到特征空间F的映射,其中F属于R(m),n<<m。根据核函数技术有:
K(xi,xj) =<Φ(xi),Φ(xj) >
其中:<, >为内积,K(xi,xj)为核函数。从上式可以看出,核函数将m维高维空间的内积运算转化为n维低维输入空间的核函数计算,从而巧妙地解决了在高维特征空间中计算的“维数灾难”等问题,从而为在高维特征空间解决复杂的分类或回归问题奠定了理论基础。
特点编辑
核函数方法的广泛应用,与其特点是分不开的:
(1)核函数的引入避免了“维数灾难”,大大减小了计算量。而输入空间的维数n对核函数矩阵无影响,因此,核函数方法可以有效处理高维输入。
(2)无需知道非线性变换函数Φ的形式和参数.
(3)核函数的形式和参数的变化会隐式地改变从输入空间到特征空间的映射,进而对特征空间的性质产生影响,最终改变各种核函数方法的性能。
(4)核函数方法可以和不同的算法相结合,形成多种不同的基于核函数技术的方法,且这两部分的设计可以单独进行,并可以为不同的应用选择不同的核函数和算法。
常见分类编辑
核函数的确定并不困难,满足Mercer定理的函数都可以作为核函数。常用的核函数有:线性核函数,多项式核函数,径向基核函数,Sigmoid核函数等,这些核函数的表达式如下:

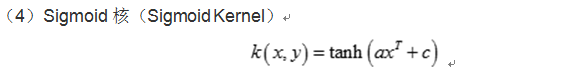
参考网站:http://blog.csdn.net/zouxy09/article/details/17291543
参考书:Python机器学习
学海无涯,博客有道!拜读咯!
Pingback引用通告: Python与人工智能 – 飞谷云人工智能