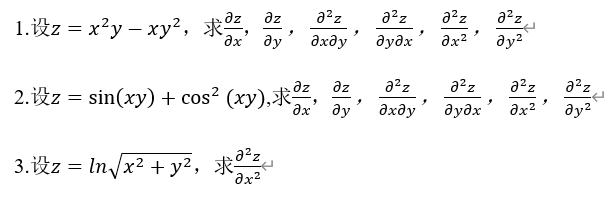第2章 多元函数微积分

2.1一阶偏导数

前面主要介绍了一元函数，在机器学习中，要处理的函数大多是多元函数（如函数y=f(x_1,x_2,\cdots,x_n)）。因此，我们需要把导数、微分拓展到多元函数上。
对多元函数如何求导呢？最简单有效的方法就是把多元微分转换为一元微分，具体实现方法就是每次只改变一个变量，其他变量的值固定不变，由此得到偏导数。
偏导数是多元函数对每个自变量的求导，对于多元函数y=f(x_1,x_2,\cdots,x_n)，它在(x_1,x_2,\cdots,x_n)点处对x_i的偏导数定义为下式的极限。
\frac{\partial y}{\partial x}=\underset{\Delta x_i \to 0}{lim}\frac{f(x_1,\cdots,x_i+\Delta x_i,\cdots,x_n)-f(x_1,\cdots,x_i,\cdots,x_n)}{\Delta x_i} \tag{2.1}
这与导数的定义相同，其中\partial为偏导数符合。为计算\frac{\partial y}{\partial x_i}，我们可以简单把变量x_i外的变量x_1,\cdots,x_{i-1},x_{i+1}\cdots,x_n作为常量，并计算y关于x_i的导数。对于偏导数的表示，以下几个表示方式是等价的：
\frac{\partial y}{\partial x_i}=\frac{\partial f}{\partial x_i}=f_{x_i}=f_i=D_i f
偏导数的几何意义，如图2-1所示，这里以一个二元函数为例，假设z=f(x,y),
则偏导\frac{\partial}{\partial x}f(x,y_0) 在点(x_0,y_0)值就是曲线z=f(x,y_0)在点(x_0,y_0)的切线斜率。

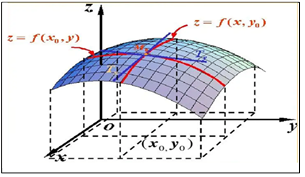
图2-1 偏导数的几何意义
例1 求函数z=x^2+3xy+y-1，求\frac{\partial z}{\partial x}和\frac{\partial z}{\partial y}在点（4，-5）的值。
解：求\frac{\partial z}{\partial x}，把y看作常量，然后对x求导。
\frac{\partial z}{\partial x}=\frac{\partial}{\partial x} (x^2+3xy+y-1)=2x+3y
\frac{\partial z}{\partial x}在点（4，-5）的值为：2\times4+3\times(-5)=-7
同理可得，\frac{\partial z}{\partial y}在点（4，-5）的值为：13

2.2 高阶偏导数

对偏导数继续求偏导数可以得到高阶偏导数，比一元函数的高阶导数复杂，每次求导时可以对多个变量进行求导，因此有多种组合。对多元函数y=f(x_1,x_2,\cdots,x_n)的二阶导数，可以先对x_i求偏导数，得到\frac{\partial y}{\partial x_i}，然后将此一阶偏导数对x_j继续求偏导数。
\frac{\partial^2 y}{\partial x_j\partial x_i}=\frac{\partial}{\partial x_j}(\frac{\partial y}{\partial x_i})
如果二阶混合偏导数连续，则与求导顺序无关，即有：
\frac{\partial^2 y}{\partial x_j\partial x_i}=\frac{\partial^2 y}{\partial x_i\partial x_j}
例2：求函数f(x,y)=x^2+xy-y^2
（1）一阶偏导
（2）二阶偏导
解：（1）一阶偏导有：
\frac{\partial f}{\partial x}=2x+y
\frac{\partial f}{\partial y}=x-2y
（2）二阶偏导有：
\frac{\partial^2 f}{\partial x^2}=\frac{\partial}{\partial x}(2x+y)=2
\frac{\partial^2 f}{\partial x\partial y}=\frac{\partial}{\partial y}(2x+y)=1
\frac{\partial^2 f}{\partial y\partial x}=\frac{\partial}{\partial x}(x-2y)=1
\frac{\partial^2 f}{\partial y^2}=\frac{\partial}{\partial y}(x-2y)=-2
如果二阶混合偏导数连续，则与求导次序无关，即有：
\frac{\partial^2 f}{\partial x\partial y}=\frac{\partial^2 f}{\partial y\partial x}

2.3多元复合函数的链式法则

多元复合函数求导的链式法则是一元函数链式法则的推广。首先，我们看二元函数的情况，注意需要对相关的全部中间变量（如下例中u和v）应用链式法则。假设z=f(u,v),u=g(x,y),v=h(x,y),则z对x，y的偏导导数为：
\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u} \frac{\partial u}{\partial x} +\frac{\partial z}{\partial v} \frac{\partial v}{\partial x}
同理
\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u} \frac{\partial u}{\partial y} +\frac{\partial z}{\partial v} \frac{\partial v}{\partial y}
\frac{\partial z}{\partial x}的求导过程如图2-2所示。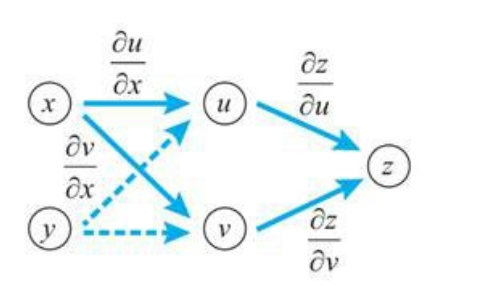

图2-2 多元复合函数的链式法则
练习：