第7章 矩阵分解的应用
矩阵分解的过程是对数据的压缩,期间通过点积运算,把数据之间的关系,通过几个更简单的矩阵来呈现,因此可以得到更加精炼的表示并去除掉一些干扰和异常。其中SVD在信息检索(隐性语义索引)、图像压缩、推荐系统、目标检测、金融服务等领域都有应用
7.1 SVD应用于推荐系统
推荐系统中往往需要计算物品之间(或用户之间)的相似度,然后把相似度最大值给用没有评分的物品,以此作为对用户对新物品的喜爱程度。
但物品与用户构成的矩阵通常较大而且稀疏,直接基于原矩阵计算物品或用户相似度,效率和效果都不很理想,所以很多专家开始寻找其他方法,其中SVD或改进版本,经实践检验,不失为一个较好方法。具体做法如下:
(1)假设物品-用户矩阵为A
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
import numpy as np from numpy import linalg as la #假设行表示用户,列表示物品 A=np.array([[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5], [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3], [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0], [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0], [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0], [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0], [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1], [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4], [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2], [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0], [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0], [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]) |
(2)对A进行SVD
|
1 2 3 4 5 6 7 8 |
#对矩阵A进行SVD U,D,VT=np.linalg.svd(A) #计算前4个奇异值的得分 total=np.sum(D**2) score_4=np.sum(D[:4]**2)/total print("前4奇异值得分:{:.2f}".format(score_4)) #前4奇异值得分:0.96 |
(3)定义计算物品之间相似度的函数
|
1 2 3 4 5 6 7 8 9 10 11 |
def ecludSim(inA,inB): return 1.0/(1.0 + la.norm(inA - inB)) def pearsSim(inA,inB): if len(inA) < 3 : return 1.0 return 0.5+0.5*np.corrcoef(inA, inB, rowvar = 0)[0][1] def cosSim(inA,inB): num = np.dot(inA.T,inB) denom = la.norm(inA)*la.norm(inB) return 0.5+0.5*(num/denom) |
(4)计算压缩后的V(该矩阵对应物品信息),并计算物品2与其它物品之间的相似度。
由 可得
可得
|
1 2 3 4 5 6 7 8 9 |
#压缩后的V V=np.dot(np.dot(A.T,U[:,:4]),np.eye(4)*D[:4]) #计算物品2与其它物品之间的相似度 n = A.shape[1] for j in range(n): if j==2: continue similarity = cosSim(V[2,:].T,V[j,:].T) print("物品2与物品{:}的相似度:{:}".format(j,similarity)) |
运行结果:
物品2与物品0的相似度:0.9999996158310511
物品2与物品1的相似度:0.999999886642839
物品2与物品3的相似度:0.5092740977256969
物品2与物品4的相似度:0.5100370458545834
物品2与物品5的相似度:0.5109165651201468
物品2与物品6的相似度:0.5053846892190899
物品2与物品7的相似度:0.999381759332992
物品2与物品8的相似度:0.9999915344456692
物品2与物品9的相似度:0.5111029802612934
物品2与物品10的相似度:0.5691678300499748
采用SVD方法计算物品之间的相似度简单高效,特别适合一些大又稀疏的矩阵。如果要计算用户之间的相似度,可以利用U矩阵。
7.2 SVD应用于图像压缩
利用公式:

对原图进行压缩,选择 实现对图像的压缩。具体步骤如下:
实现对图像的压缩。具体步骤如下:
(1)导入需要的库
|
1 2 3 4 |
import numpy as np from numpy.linalg import svd from PIL import Image import matplotlib.pyplot as plt |
(2)可视化原图(大家可用自己的图替换)
|
1 2 3 4 5 6 7 8 |
#定义图像存放路径 image_path='./data/cat/' image = Image.open(image_path+"cat.1.jpg") image = np.array(image) print(np.shape(image)) plt.title("原图像") plt.imshow(image) |
运行结果:
(414, 500, 3)

(3)对图像进行压缩
该图片的通道数为3,说明是一张彩色图像。对彩色图像进行SVD时,分别对R、G、B三个通道进行。
|
1 2 3 4 5 6 7 8 9 10 |
def compression(image,k): image2 = np.zeros_like(image) rat3=0 for i in range(image.shape[2]): U, S, Vt = svd(image[:,:,i]) image2[:,:,i] = U[:,:k].dot(np.diag(S[:k])).dot(Vt[:k,:]) rat=np.sum(S[:k]**2)/np.sum(S[:]**2) rat3+=rat plt.imshow(image2) plt.title('压缩后的图像,k = %s,rat=%d'% (k,rat3*100/3)) |
(4)运行
|
1 |
compression(image,10) |
运行结果
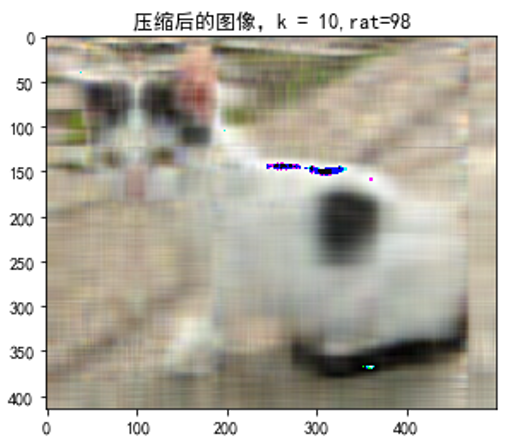
这里取前10个奇异值,得到保留原图像的信息量达98%。
7.3 SVD目标检测中
在Fast R-CNN目标检测或图像处理中,输入或输出图像像素一般较大,而且要处理的图像很多,如果用全连接,则参数量将非常大。这时我们可以采用矩阵压缩技术,这种压缩,既能保留原图像的巨大部分信息,又可大大降维矩阵的维度,从而大大降低计算量。如下图所示。
其中
对y=Wx中权重参数矩阵W用UΣV^T替换,即:

从上式可以很容易的看出,用两个全连接层近似替代一个全连接层,两个全连接层的参数分别为 和U,如下图所示:
和U,如下图所示: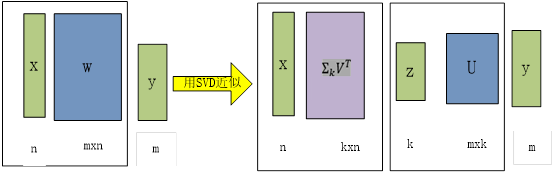
当k比较小时,如 ,替换后的参数将由
,替换后的参数将由 降低到k(m+n),计算量也降低不少。
降低到k(m+n),计算量也降低不少。
SVD应用非常广泛,如利用视频中背景与前景变化情况,可用SVD从视频中删除背景
在NLP领域,可用上下词生成的共现矩阵,实现Wword Embedding功能等等。

![X=[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_193e348a7f28c1809cf3be796d9e2409.gif)










![Q=[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_93938b91da7f312a1d0f1d659df6d89a.gif)
![[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_5b24c69c53879fbd5f252ac017989773.gif)
![x=[x_1,x_2,\cdots,x_n][a_1,a_2,\cdots,a_n ]^T](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_54da61aa5df5c2c65fb17bb909f55636.gif)
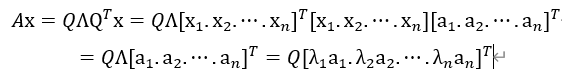
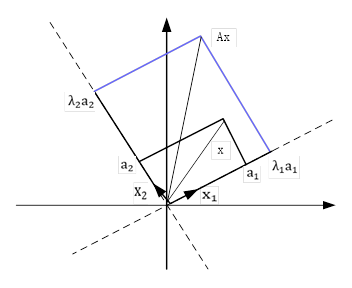
![[v_1,v_2,\cdots,v_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_7b34aa5991785b3ab206ef9057dc99b9.gif)
![[Av_1,Av_2,\cdots,Av_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_3d5b0cb07ab9017032eed69d58a5addb.gif)

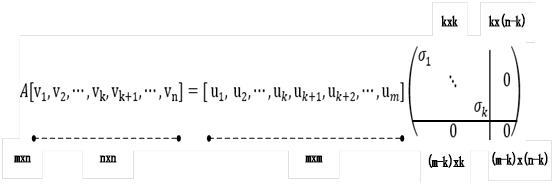








![[u_1,u_2,\cdots,u_k]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_8b50705cfc07cea81ceb9a5d7b6e41b5.gif)
![[v_1,v_2,\cdots,v_k]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_03a5b82985c7a666ebaf3df2f688baea.gif)





![[v^1,v^2,\cdots,v^n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_33046d9a881830901d8dbd465bc032f1.gif)
![[\lambda_1,\lambda_2,\cdots,\lambda_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_bfaa2482f208825de2d1fa0ba296ae8d.gif)
![V=[v^1,v^2,\cdots,v^n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_2700ee472dbfa152766c8bacee1f685c.gif)





















![\left[\left(\begin{matrix}1&2 \\ 0 &{-1} \end{matrix}\right)-\lambda \left(\begin{matrix}1&0 \\ 0&1 \end{matrix}\right)\right]=0](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_b046ef3b8842d01335033942f3be0e6a.gif)
![\left[\left(\begin{matrix}1&2 \\ 0 &{-1} \end{matrix}\right)-\left(\begin{matrix}\lambda &0 \\ 0&\lambda\end{matrix}\right)\right]=0](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_13aaa58fe526c17fb8e388c3f2701a67.gif)
![\left[\begin{matrix}{1-\lambda}&2 \\ 0 &{-1-\lambda} \end{matrix}\right]=0](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_a6409c423536da595e2dfd4575c97ba7.gif)




![a=[a_1,a_2,\cdots,a_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_7580eb047fc7e8965f7cf6ade12c1f28.gif)
![b=[b_1,b_2,\cdots,b_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_97b19c4c617a7c377e1b76947d977621.gif)



![e=[e_1,e_2,\cdots,e_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_939995464ea64eaf49dfc487d512ea3e.gif)

![a=[a_1,a_2,\cdots,a_n ]=a\cdot e](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_ff16788a3c01e200e1fd1746f678d9e5.gif)
























![X=\left[\begin{matrix} 1&0\\0&2\\0&0\end{matrix}\right]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_d2f59da831f63960df062b81d88c92dd.gif)
![diag(v)=diag([v_1,v_2,\cdots,v_n]^T) \tag{2.14}](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_7b808bdff924076375dc309e9167972c.gif)
![v=[v_1,v_2,\cdots,v_n]^T](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_f97782776ea99bbeabed0b72a74c97ed.gif)
![v=[v_1,v_2,\cdots,v_n]^T,x=[x_1,x_2,\cdots,x_n]^T](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_a80954bbcbbf9ed04dbcb7c68cdfef7a.gif)

![diag(v)^{-1}=diag([1/v_1,1/v_2,\cdots,1/v_n]^T)](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_8499f5b16280c8e74d3147804496857b.gif)









