第5章 特征值和特征向量
特征值(Eigenvalue,又称为本征值)与特征向量(Eigenvector,又称为本征向量)决定了矩阵的很多特性。
5.1 特征值和特征向量的定义
设A是一个n阶方阵,如果存在实数λ和n维的非零向量x,满足

那么把数λ称为方阵A的特征值,向量x称为属于特征值λ的特征向量。
对式(5.1)进行恒等变换,把 移到左边,得到下式:
移到左边,得到下式:

为便于计算,把 写成
写成 ,其中E是n阶单位矩阵。式(5.2)可写成:
,其中E是n阶单位矩阵。式(5.2)可写成:

提取向量x,可得下式:

其中 称为A的特征矩阵,要使式(5.3)有非零解,特征矩阵的行列式为0(如果行列式不等于0,x只要0解)
称为A的特征矩阵,要使式(5.3)有非零解,特征矩阵的行列式为0(如果行列式不等于0,x只要0解)
令特征矩阵构成的行列式等于0得:

式(5.4)称为特征方程。通过特征方程可以求出特征值,把求出的特征值代入式(5.3)可以求出特征值对应的特征向量。
5.2 求特征值与特征向量的实例
例1:求矩阵A的特征值、特征向量。

解:
(1)生成特征方程,即: ,代入矩阵A的值,得:
,代入矩阵A的值,得:
![\left[\left(\begin{matrix}1&2 \\ 0 &{-1} \end{matrix}\right)-\lambda \left(\begin{matrix}1&0 \\ 0&1 \end{matrix}\right)\right]=0](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_b046ef3b8842d01335033942f3be0e6a.gif)
化简得:
![\left[\left(\begin{matrix}1&2 \\ 0 &{-1} \end{matrix}\right)-\left(\begin{matrix}\lambda &0 \\ 0&\lambda\end{matrix}\right)\right]=0](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_13aaa58fe526c17fb8e388c3f2701a67.gif)
![\left[\begin{matrix}{1-\lambda}&2 \\ 0 &{-1-\lambda} \end{matrix}\right]=0](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_a6409c423536da595e2dfd4575c97ba7.gif)
由此可得:

解上式方程,可得:特征值 或
或
(2)把特征值 ,代入下式:
,代入下式:
用python实现以上计算过程:
|
1 2 3 4 5 6 7 8 9 |
import numpy as np a = np.array([[1,2],[0,-1]]) # 示例矩阵 A1 = np.linalg.eigvals(a) # 得到特征值 A2,V1 = np.linalg.eig(a) # 其中A2也是特征值,V1为特征向量 print("特征值:",A1) print("特征值:",A2) print("特征向量构成的矩阵:") print(V1) |
运行结果:
特征值: [ 1. -1.]
特征值: [ 1. -1.]
特征向量构成的矩阵:
[[ 1. -0.70710678]
[ 0. 0.70710678]]
【说明】
在numpy.linalg模块中:
eigvals() 计算矩阵的特征值
eig() 返回包含特征值和对应特征向量的元组
5.3 点积的几何意义
这里矩阵A的功能有点特殊,竟然把一个向量变为一个仅相差一个乘数λ的向量。
矩阵与向量相乘(或矩阵与矩阵相乘)的具体功能或其几何意义是什么?
其实不管是向量和向量的点积,还是矩阵与向量的点积都是点积运算。只要理解了点积运算的本质,其它都如此。为此我们先看点积运算的几何意义。
1)向量与向量点积运算几何意义
假设有两个向量a,b:
![a=[a_1,a_2,\cdots,a_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_7580eb047fc7e8965f7cf6ade12c1f28.gif)
![b=[b_1,b_2,\cdots,b_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_97b19c4c617a7c377e1b76947d977621.gif)
在欧几里得空间中,向量a、b的点积可以直观地定义为

这里|a|表示a的长度,θ为a与b之间的夹角。其相应的几何表示为:
如果b为单位向量,即|b|=1,则

此时a与b的内积就是a在b上投影。
实际上我们的向量a表示就是它在对应正交基上的投影。假设![e=[e_1,e_2,\cdots,e_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_939995464ea64eaf49dfc487d512ea3e.gif) 为
为 空间中一个标准正交基。则有
空间中一个标准正交基。则有
![a=[a_1,a_2,\cdots,a_n ]=a\cdot e](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_ff16788a3c01e200e1fd1746f678d9e5.gif)
其中 就是a在
就是a在 上的投影。
上的投影。
如果向量a、b互相垂直,那么它们的内积为0,如果它们在一条直线上且同方向,它们的内积最大(假设a、b的模都为1)。由此可知,向量的内积实际上说明了这两个向量之间的相似程度。
【说明】点积的几何解释通常只适用于 。在高维空间,其他的域或模中,点积只有一个定义,那就是:
。在高维空间,其他的域或模中,点积只有一个定义,那就是:

2)矩阵与向量点积的几何意义
(1)如果 ,
, , 矩阵A与向量x的点积,通过矩阵A作用后,X变为
, 矩阵A与向量x的点积,通过矩阵A作用后,X变为 ,为:
,为:

相当于把特征向量X在 方向上进行了拉伸,拉伸了2倍,
方向上进行了拉伸,拉伸了2倍, 方向不变。如下图所示。
方向不变。如下图所示。

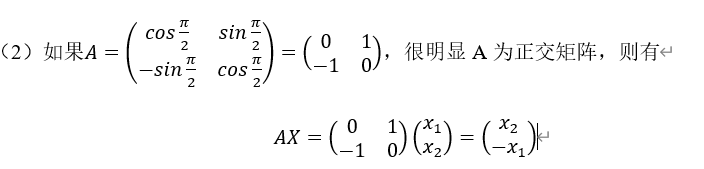
相当于把向量X进行顺时针旋转 度,如下图所示。
度,如下图所示。

这里是旋转 ,实际上可以选择任何角度
,实际上可以选择任何角度 ,这时只有把矩阵A定义为
,这时只有把矩阵A定义为
 。
。
由上可知,作为n阶矩阵这里就相当于一个线性变换(拉伸或旋转),矩阵这种作用在机器学习中非常普遍。
回到特征值的定义:Ax=λx可以看出,特征向量通过矩阵A的线性变换之后仍然处于同一条直线上,只是对特征向量x的进行拉伸,拉伸比例就是特征值λ。
5.4 内积的内涵
根据特征向量的定义,如果x为矩阵A的特征向量,则有:
Ax=λx
Ax是内积运算,而内积运算实际上反映了它们之间一种相似程度,而这个相似程度实际已经用特征值λ表示了。所以我们可以说,正是因为正在内积运算才能使特征值和特征向量揭示矩阵A本身的很多特性,这或许就是特征(Eigen,其含义为本身的意思)来描述这种情况的原因之一。通过矩阵A的特征值,我们可以发现很多有趣的情况,如对特征值进行降序,特征值较大可代表矩阵A的信息量就大,信息量还可进行量化。
其实在机器学习领域,很多数据集都可以看成是矩阵,如一张图像、一份结构化数据、一篇文章等等,通过数字化后,实际都是一个矩阵。而特征值或特征向量能很好代表矩阵的特征,所以,研究矩阵的特征值就显得非常有意义了。如何找出矩阵的特征值呢?方法很多,其中矩阵分解是常用方法之一。