用简单方法学会—-参数估计 | Python技术交流与分享

4.6 参数估计

参数估计（parameter estimation）是根据从总体中抽取的样本估计总体分布中包含的未知参数的方法。人们常常需要根据手中的数据，分析或推断数据反映的本质规律。即根据样本数据如何选择统计量去推断总体的分布或数字特征等。统计推断是数理统计研究的核心问题。所谓统计推断是指根据样本对总体分布或分布的数字特征等作出合理的推断。它是统计推断的一种基本形式，是数理统计学的一个重要分支。
参数估计有最大似然估计和EM算法，他们都是在已知样本数据下，如何确定未知参数的值，才能使样本值最大。而他们的区别是EM是带隐变量的似然估计，当有部分数据缺失或者无法观察到时，EM算法提供了一个高效的迭代程序用来计算这些数据的最大似然估计。

4.6.1极大似然估计

4.6.1.1极大似然估计简介

极大似然估计是一种参数估计的方法。
先验概率是知因求果，后验概率是知果求因，极大似然是知果求最可能的原因。
即它的核心思想是：找到参数 θ的一个估计值，使得当前样本出现的可能性最大。

例如，当其他条件一样时，抽烟者患肺癌的概率是不抽烟者的 5 倍，那么当我们已知现在有个人是肺癌患者，问这个人是抽烟还是不抽烟？大多数人都会选择抽烟，因为这个答案是“最有可能”得到“肺癌”这样的结果。

4.6.1.2 为什么要有参数估计

当模型已定，但是参数未知时。
例如我们知道全国人民的身高服从正态分布，这样就可以通过采样，观察其结果，然后再用样本数据的结果推出正态分布的均值与方差的大概率值，就可以得到全国人民的身高分布的函数。

4.6.1.3为什么要用似然函数取最大

极大似然估计是频率学派最经典的方法之一，认为真实发生的结果的概率应该是最大的，那么相应的参数，也应该是能让这个状态发生的概率最大的参数。

4.6.1.4何为似然函数

统计学中，似然（likelihood）函数是一种关于统计模型参数的函数。给定输出x时，关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ后变量X的概率：L(θ|x)=P(X=x|θ)。
如果有n个样本,似然函数为：
设总体X服从分布P(x；θ)（当X是连续型随机变量时为概率密度，当X为离散型随机变量时为概率分布），θ为待估参数，X1,X2,…Xn是来自于总体X的样本，x1,x2…xn为样本X1,X2,…Xn的一个观察值，则样本的联合分布（当X是连续型随机变量时为概率密度，当X为离散型随机变量时为概率分布）　L(θ)=L(x1,x2,…,xn;θ)=ΠP(xi;θ)称为似然函数.

4.6.1.5极大似然估计的计算过程

(1)写出似然函数：

其中 x1,x2,..,xn 为样本，θ 为要估计的参数。

(2) 一般对似然函数取对数

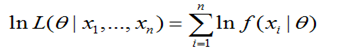
为何要两边取对数？因为 f(xi|θ) 一般比较小，n 比较大，如果连乘容易造成浮点运算下溢。
(3) 求出使得对数似然函数取最大值的参数值
对对数似然函数求导，令导数为0，得出似然方程，
求解似然方程，得到的参数就是对概率模型中参数值的极大似然估计。
（4）示例
假如一个罐子里有黑白两种颜色的球，数目和比例都不知道。
假设进行一百次有放回地随机采样，每次取一个球，有七十次是白球。
问题是要求得罐中白球和黑球的比例？

假设罐中白球的比例是 p，那么黑球的比例就是 1-p。
第1步：定义似然函数：

第2步：对似然函数对数化

第3步：求似然方程
即对参数p求导，并令导数为0。

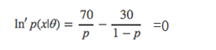
第4步解方程
最后求得 p=0.7

4.6.2 EM算法

EM（Expectation Maximization）算法是 Dempster,Laind,Rubin 于 1977 年提出的求参数极大似然估计的一种方法，它可以从非完整数据集中对参数进行 MLE 估计，是一种非常简单实用的学习算法。这种方法可以广泛地应用于处理缺损数据，截尾数据，带有噪声等所谓的不完全数据。
EM的主要原理可以用一个比较形象的比喻说法。比如说食堂的大师傅炒了一份菜，要等分成两份给两个人吃，显然没有必要拿来天平一点的精确的去称分量，最简单的办法是先随意的把菜分到两个碗中，然后观察是否一样多，把比较多的那一份取出一点放到另一个碗中，这个过程一直迭代地执行下去，直到大家看不出两个碗所容纳的菜有什么分量上的不同为止。
EM算法就是这样，假设我们估计知道A和B两个参数，在开始状态下二者都是未知的，并且知道了A的信息就可以得到B的信息，反过来知道了B也就得到了A。可以考虑首先赋予A某种初值，以此得到B的估计值，然后从B的当前值出发，重新估计A的取值，这个过程一直持续到收敛为止。

4.6.2.1简单回顾最大似然估计

极大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。最大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

4.6.2.2求最大似然函数估计值的一般步骤

（1）写出似然函数；
（2）对似然函数取对数，并整理；
（3）求导数，令导数为0，得到似然方程；
（4）解似然方程，得到的参数即为所求；

4.6.2.3生活中EM原型

在上面那个身高分布估计中。男生的身高服从高斯分布、女生身高也服从高斯分布，只是他们的参数可能不相同，那么通过抽取得到的那100个男生的身高和已知的其身高服从高斯分布，我们通过最大化其似然函数，就可以得到了对应高斯分布的参数θ=[u, ∂]T了。那么，对于我们学校的女生的身高分布也可以用同样的方法得到了。
上面这个例子，我们知道抽取的男生还是女生，即知道其分布（都是高斯分布，虽然不知分布的具体参数），现在假如我们从这200个人中，这200人，由于化妆的原因，我们无法确定这个人（的身高）是男生（的身高）还是女生（的身高）。也就是说你不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的，还是女生的那个身高分布抽取的。用数学的语言就是，抽取得到的每个样本都不知道是从哪个分布抽取的。
这个时候，对于每一个样本或者你抽取到的人，就有两个东西需要猜测或者估计的了，一是这个人是男的还是女的？二是男生和女生对应的身高的高斯分布的参数是多少？
只有当我们知道了哪些人属于同一个高斯分布的时候，我们才能够对这个分布的参数作出靠谱的预测，例如刚开始的最大似然所说的，但现在两种高斯分布的人混在一块了，我们又不知道哪些人属于第一个高斯分布，哪些属于第二个，所以就没法估计这两个分布的参数。反过来，只有当我们对这两个分布的参数作出了准确的估计的时候，才能知道到底哪些人属于第一个分布，那些人属于第二个分布。
如何这类互相依赖问题呢？这有点像先有鸡还是先有蛋的问题了。鸡说，没有我，谁把你生出来的啊。蛋不服，说，没有我，你从哪蹦出来啊。为了解决这个你依赖我，我依赖你的循环依赖问题，总得有一方要先打破僵局，说，不管了，我先随便整一个值出来，看你怎么变，然后我再根据你的变化调整我的变化，然后如此迭代着不断互相推导，最终就会收敛到一个解。这就是EM算法的基本思想了。
EM的意思是“Expectation Maximization”，在我们上面这个问题里面，我们是先随便猜一下男生（身高）的正态分布的参数：如均值和方差是多少。例如男生的均值是1米7，方差是0.1米（当然了，刚开始肯定没那么准），然后计算出每个人更可能属于第一个还是第二个正态分布中的（例如，这个人的身高是1米8，那很明显，他最大可能属于男生的那个分布），这个是属于Expectation一步。有了每个人的归属，或者说我们已经大概地按上面的方法将这200个人分为男生和女生两部分，我们就可以根据之前说的最大似然那样，通过这些被大概分为男生的n个人来重新估计第一个分布的参数，女生的那个分布同样方法重新估计。这个是Maximization。然后，当我们更新了这两个分布的时候，每一个属于这两个分布的概率又变了，那么我们就再需要调整E步……如此往复，直到参数基本不再发生变化为止。
这里把每个人（样本）的完整描述看做是三元组yi={xi,zi1,zi2}，其中，xi是第i个样本的观测值，也就是对应的这个人的身高，是可以观测到的值。zi1和zi2表示男生和女生这两个高斯分布中哪个被用来产生值xi，就是说这两个值标记这个人到底是男生还是女生（的身高分布产生的）。这两个值我们是不知道的，是隐含变量。确切的说，zij在xi由第j个高斯分布产生时值为1，否则为0。例如一个样本的观测值为1.8，然后他来自男生的那个高斯分布，那么我们可以将这个样本表示为{1.8, 1, 0}。如果zi1和zi2的值已知，也就是说每个人我已经标记为男生或者女生了，那么我们就可以利用上面说的最大似然算法来估计他们各自高斯分布的参数。但是它们未知，因此我们只能用EM算法。
咱们现在不是因为那个恶心的隐含变量（抽取得到的每个样本都不知道是从哪个分布抽取的）使得本来简单的可以求解的问题变复杂了，求解不了吗。那怎么办呢？人类解决问题的思路都是想能否把复杂的问题简单化。好，那么现在把这个复杂的问题逆回来，我假设已经知道这个隐含变量了，哎，那么求解那个分布的参数是不是很容易了，直接按上面说的最大似然估计就好了。那你就问我了，这个隐含变量是未知的，你怎么就来一个假设说已知呢？你这种假设是没有根据的。呵呵，我知道，所以我们可以先给这个给分布弄一个初始值，然后求这个隐含变量的期望，当成是这个隐含变量的已知值，那么现在就可以用最大似然求解那个分布的参数了吧，那假设这个参数比之前的那个随机的参数要好，它更能表达真实的分布，那么我们再通过这个参数确定的分布去求这个隐含变量的期望，然后再最大化，得到另一个更优的参数，……迭代，就能得到一个皆大欢喜的结果了。
这时候你就不服了，说你老迭代迭代的，你咋知道新的参数的估计就比原来的好啊？为什么这种方法行得通呢？有没有失效的时候呢？什么时候失效呢？用到这个方法需要注意什么问题呢？呵呵，一下子抛出那么多问题，搞得我适应不过来了，不过这证明了你有很好的搞研究的潜质啊。呵呵，其实这些问题就是数学家需要解决的问题。在数学上是可以稳当的证明的或者得出结论的。那咱们用数学来把上面的问题重新描述下。（在这里可以知道，不管多么复杂或者简单的物理世界的思想，都需要通过数学工具进行建模抽象才得以使用并发挥其强大的作用，而且，这里面蕴含的数学往往能带给你更多想象不到的东西，这就是数学的精妙所在啊）。

4.6.2.4 EM算法推导

假设我们有一个样本集{x(1),…,x(m)}，包含m个独立的样本。但每个样本i对应的类别z(i)是未知的（如，不知道它属于哪种分布），也即隐含变量。故我们需要估计概率模型p(x,z)的参数θ，但是由于里面包含隐含变量z，所以很难用最大似然求解，但如果z知道了，那我们就很容易求解了。
对于参数估计，我们本质上还是想获得一个使似然函数最大化的那个参数θ，现在与最大似然不同的只是似然函数式中多了一个未知的变量z，见下式（1）。也就是说我们的目标是找到适合的θ和z让L(θ)最大。那我们也许会想，你就是多了一个未知的变量而已啊，我也可以分别对未知的θ和z分别求偏导，再令其等于0，求解出来不也一样吗？

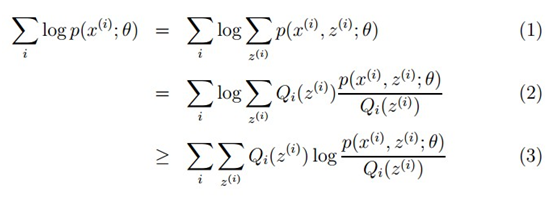
本质上我们是需要最大化（1）式（对（1）式，我们回忆下联合概率密度下某个变量的边缘概率密度函数的求解，注意这里z也是随机变量。对每一个样本i的所有可能类别z求等式右边的联合概率密度函数和，也就得到等式左边为随机变量x的边缘概率密度），也就是似然函数，但是可以看到里面有“和的对数”，求导后形式会非常复杂（自己可以想象下log(f1(x)+ f2(x)+ f3(x)+…)复合函数的求导），所以很难求解得到未知参数z和θ。那OK，我们可否对（1）式做一些改变呢？我们看（2）式，（2）式只是分子分母同乘以一个相等的函数，还是有“和的对数”啊，还是求解不了，那为什么要这么做呢？咱们先不管，看（3）式，发现（3）式变成了“对数的和”，那这样求导就容易了。我们注意点，还发现等号变成了不等号，为什么能这么变呢？这就是Jensen不等式的大显神威的地方。

4.6.2.5Jensen不等式

设f是定义域为实数的函数，如果对于所有的实数x。如果对于所有的实数x，f(x)的二次导数大于等于0，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的，那么f是凸函数。如果只大于0，不等于0，那么称f是严格凸函数。
Jensen不等式表述如下：
如果f是凸函数，X是随机变量，那么：E[f(X)]>=f(E[X])
特别地，如果f是严格凸函数，当且仅当X是常量时，上式取等号。
如果用图表示会很清晰：

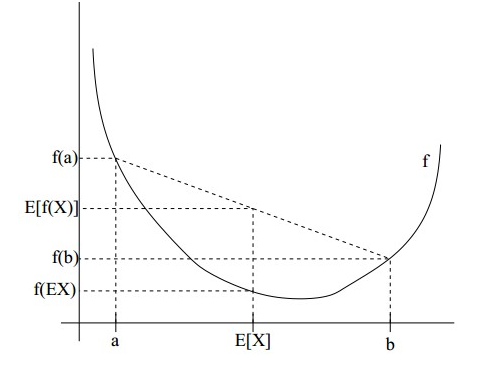
图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。（就像掷硬币一样）。X的期望值就是a和b的中值了，图中可以看到E[f(X)]>=f(E[X])成立。
当f是（严格）凹函数当且仅当-f是（严格）凸函数。
Jensen不等式应用于凹函数时，不等号方向反向。
回到公式（2），因为f(x)=log x为凹函数（其二次导数为-1/x2<0）。（2）式中

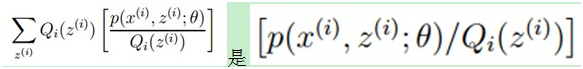
的期望，（考虑到E(X)=∑x*p(x)，f(X)是X的函数，则E(f(X))=∑f(x)*p(x)），又，所以就可以得到公式（3）的不等式了。

4.6.2.6 EM算法运算步骤4.6.2.7代码实现

4.6.2.7.1 双硬币模型

假设有两枚硬币A、B，以相同的概率随机选择一个硬币，进行如下的抛硬币实验：共做5次实验，每次实验独立的抛十次，结果如图中a所示，例如某次实验产生了H、T、T、T、H、H、T、H、T、H，H代表正面朝上。
假设试验数据记录员可能是实习生，业务不一定熟悉，造成a和b两种情况
a表示实习生记录了详细的试验数据，我们可以观测到试验数据中每次选择的是A还是B
b表示实习生忘了记录每次试验选择的是A还是B，我们无法观测实验数据中选择的硬币是哪个。问在两种情况下分别如何估计两个硬币正面出现的概率？

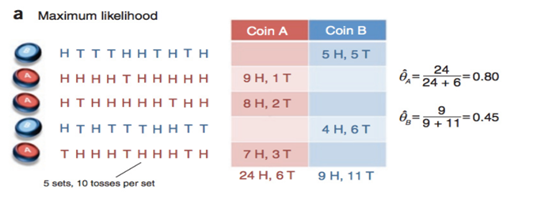
这是实习生a记录的情况，由于这里数据的背后参考模型已知（已分好类），因此用极大似然估计方法就能分别求出θ ̂_A和θ ̂_B的概率来。与上文第一节中的例子完全类似。

上图为实习生b记录的情况，令人遗憾的是数据的背后参考模型混淆在了一起，我们无法得知它们这几组实验数据是由A抛的还是由B抛的，因为这里隐含了一个该组数据是A还是B的分类问题。抛开数学对隐含变量的复杂求解过程，我们可以先给出一个思路来解决上述问题。
第一，既然我们不清楚是A类还是B类，但假定我们初始化了A类硬币抛正面的概率和B类硬币抛正面的概率，这两者的概率是随意定的，但由于两者概率可以存在差异，假设P(y=H;θA)>P(y=H;θB)，那么一个明显的特征就是，由于能观察到10次硬币中有几次是成功的，我们可以基于这次观察，给出P(z=A|Y;θA,θB)的概率，上式的含义是可以根据两个参数的初值求出，在给定观察序列的情况下，它属于A类还是B类的概率。用公式可以表示为：

其中，z表示单个观察到的随机变量，此处z=A or B（属于分类问题），Y表示观察序列，即Y=(y1,y2,...,y10)T。由此，给定观察序列后，我们可以算出属于A类的概率和属于B类的概率，那么很显然CoinA 和CoinB 不再是属于你有我没有，你没有我有的敌对关系，因为我自己都还不是很清楚是不是A类，由此10个硬币，我们就根据概率进行一次平均分配咯，这样CoinA 和CoinB 在一次观察结果时，都能得到属于自己的那一份，非常的和谐。这一部分便是求期望的过程，即对于第一个观察序列中，10次抛硬币过程中5次为正面朝上，令yj=5，由此可以得到关于隐含变量的数学期望E(z)=0.45*5+0.55*5，其中0.45*5表示CoinA的分配; 0.55*5表示CoinB的分配。分配的份额根据z函数的分布给定，z函数的分布规则根据缺失的信息进行建模，解由初始参数求出。
因此分类问题，给出了每个CoinA 和CoinB 的分配额，有了所有观察值CoinA和CoinB的分配额，我们就可以单独的对CoinA和CoinB进行最大似然估计方法。求出来的新参数，再求z函数，求期望，求参数，如此迭代下去，直到收敛到某一结果。

4.6.2.7.2导入必要的库

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
from ipywidgets import interact, FloatSlider
%matplotlib inline

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt

import seaborn as sns

from ipywidgets import interact, FloatSlider

%matplotlib inline

4.6.2.7.2编写伯努利分布函数

在双硬币模型中，对某个种类硬币投掷10次中成功n次概率模型

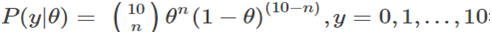
符合伯努利分布

a=range(11)
def plot_binomial(p=0.5):
    fig, ax = plt.subplots(figsize=(4,3))
    y = [0]*11
    for i in a:
        y[i] =  stats.binom.pmf(i, 10, p)
    ax.bar(a,y,label="$p = %.1f$" % p)
    ax.set_ylabel('PMF of $k$ heads')
    ax.set_xlabel('$k$')
    ax.set_ylim((0,0.5))
    ax.set_xlim((0,10))
    ax.legend()
    return fig

a=range(11)

def plot_binomial(p=0.5):

fig, ax = plt.subplots(figsize=(4,3))

y = [0]*11

for i in a:

y[i] = stats.binom.pmf(i, 10, p)

ax.bar(a,y,label="$p = %.1f$" % p)

ax.set_ylabel('PMF of $k$ heads')

ax.set_xlabel('$k$')

ax.set_ylim((0,0.5))

ax.set_xlim((0,10))

ax.legend()

return fig

可视化伯努利分布

interact(plot_binomial, p=FloatSlider(min=0.0,max=1.0,step=0.1,value=0.2))

1	interact(plot_binomial, p=FloatSlider(min=0.0,max=1.0,step=0.1,value=0.2))

运行结果如下：

这是在p=0.2的情况下的伯努利分布函数，代回双硬币模型中去，当观察到10次实验中只有2次成功了，那么该θ参数便是0.2。因为只有当θ=0.2时，10次实验中出现成功次数为2次的概率最大

4.6.2.7.3 定义观察矩阵

由数据可得观察矩阵为

observations = np.array([[1,0,0,0,1,1,0,1,0,1],
                         [1,1,1,1,0,1,1,1,1,1],
                         [1,0,1,1,1,1,1,0,1,1],
                         [1,0,1,0,0,0,1,1,0,0],
                         [0,1,1,1,0,1,1,1,0,1]])

observations = np.array([[1,0,0,0,1,1,0,1,0,1],

[1,1,1,1,0,1,1,1,1,1],

[1,0,1,1,1,1,1,0,1,1],

[1,0,1,0,0,0,1,1,0,0],

[0,1,1,1,0,1,1,1,0,1]])

有实习生a记录的信息可知，实际每组观察数据属于A类，B类的隐藏状态为：

coins_id = np.array([False,True,True,False,True])

1	coins_id = np.array([False,True,True,False,True])

那么在观察数组中，属于A类的数组为：

observations[coins_id]

1	observations[coins_id]

运行结果为：
array([[1, 1, 1, 1, 0, 1, 1, 1, 1, 1],
[1, 0, 1, 1, 1, 1, 1, 0, 1, 1],
[0, 1, 1, 1, 0, 1, 1, 1, 0, 1]])
在所有属于A类的数组中，总的实验成功次数为：

np.sum(observations[coins_id])

1	np.sum(observations[coins_id])

运行结果为：24
所以说，针对属于A类的硬币，它的参数θ_A：

1.0*np.sum(observations[coins_id])/observations[coins_id].size

1	1.0*np.sum(observations[coins_id])/observations[coins_id].size

运行结果为：0.80000000000000004

同理，对于属于B类的硬币，它的参数为θ_B:

1.0*np.sum(observations[~coins_id])/observations[~coins_id].size

1	1.0*np.sum(observations[~coins_id])/observations[~coins_id].size

运行结果为：0.45000000000000001

4.6.2.7.4 EM算法步骤

（1）首先来看看，针对第一组观察数据，每一步的数据是如何求出的。
# 对于实验成功率为0.6的情况，10次中成功5次的概率

coin_A_pmf_observation_1= stats.binom.pmf(5,10,0.6)
coin_A_pmf_observation_1

# 均是针对第一组观察数据的情况
coin_B_pmf_observation_1= stats.binom.pmf(5,10,0.5)
coin_B_pmf_observation_1

# 针对第一组观察数据中，属于A类硬币投掷的概率p(z=A|Y,theta)
normalized_coin_A_pmf_observation_1 = coin_A_pmf_observation_1/(coin_A_pmf_observation_1+coin_B_pmf_observation_1)
print ("%0.2f" %normalized_coin_A_pmf_observation_1)

# 针对第一组观察数据中，属于B类硬币投掷的概率p(z=B|Y,theta)
normalized_coin_B_pmf_observation_1 = coin_B_pmf_observation_1/(coin_A_pmf_observation_1+coin_B_pmf_observation_1)
print ("%0.2f" %normalized_coin_B_pmf_observation_1)

#求期望过程
weighted_heads_A_obervation_1 = 5*normalized_coin_A_pmf_observation_1
print ("Coin A Weighted count for heads in observation 1: %0.2f" %weighted_heads_A_obervation_1)
weighted_tails_A_obervation_1 = 5*(1-normalized_coin_A_pmf_observation_1)
print ("Coin A Weighted count for tails in observation 1: %0.2f" %weighted_tails_A_obervation_1)
weighted_heads_B_obervation_1 = 5*normalized_coin_B_pmf_observation_1
print ("Coin B Weighted count for heads in observation 1: %0.2f" %weighted_heads_B_obervation_1)
weighted_tails_B_obervation_1 = 5*(1-normalized_coin_B_pmf_observation_1)
print ("Coin B Weighted count for tails in observation 1: %0.2f" %weighted_tails_B_obervation_1)

coin_A_pmf_observation_1= stats.binom.pmf(5,10,0.6)

coin_A_pmf_observation_1

# 均是针对第一组观察数据的情况

coin_B_pmf_observation_1= stats.binom.pmf(5,10,0.5)

coin_B_pmf_observation_1

# 针对第一组观察数据中，属于A类硬币投掷的概率p(z=A|Y,theta)

normalized_coin_A_pmf_observation_1 = coin_A_pmf_observation_1/(coin_A_pmf_observation_1+coin_B_pmf_observation_1)

print ("%0.2f" %normalized_coin_A_pmf_observation_1)

# 针对第一组观察数据中，属于B类硬币投掷的概率p(z=B|Y,theta)

normalized_coin_B_pmf_observation_1 = coin_B_pmf_observation_1/(coin_A_pmf_observation_1+coin_B_pmf_observation_1)

print ("%0.2f" %normalized_coin_B_pmf_observation_1)

#求期望过程

weighted_heads_A_obervation_1 = 5*normalized_coin_A_pmf_observation_1

print ("Coin A Weighted count for heads in observation 1: %0.2f" %weighted_heads_A_obervation_1)

weighted_tails_A_obervation_1 = 5*(1-normalized_coin_A_pmf_observation_1)

print ("Coin A Weighted count for tails in observation 1: %0.2f" %weighted_tails_A_obervation_1)

weighted_heads_B_obervation_1 = 5*normalized_coin_B_pmf_observation_1

print ("Coin B Weighted count for heads in observation 1: %0.2f" %weighted_heads_B_obervation_1)

weighted_tails_B_obervation_1 = 5*(1-normalized_coin_B_pmf_observation_1)

print ("Coin B Weighted count for tails in observation 1: %0.2f" %weighted_tails_B_obervation_1)

（2）单步EM算法，迭代一次算法实现步骤。

def em_single(priors,observations):
    """
    performs a single Em step
    Arguments
    ---------
    priors:[theta_A,theta_B]
    observations:[m X n matrix]

    Returns
    -------
    new_priors:[new_theta_A,new_theta_B]
    """
    counts ={'A':{'H':0,'T':0},'B':{'H':0,'T':0}}
    theta_A = priors[0]
    theta_B = priors[1]

    # E setp
    for observation in observations:
        len_observation = len(observation)
        # 对数组求和 head =1，tail =0
        num_heads = observation.sum()
        num_tails = len_observation - num_heads
        # 如果属于A类，A的分布概率 和属于B类的分布概率
        contribution_A = stats.binom.pmf(num_heads,len_observation,theta_A)
        contribution_B = stats.binom.pmf(num_heads,len_observation,theta_B)
        # z分布概率
        weight_A = contribution_A /(contribution_A+contribution_B)
        weight_B = contribution_B /(contribution_A+contribution_B)

        # Incrementing counts
        counts['A']['H'] += weight_A*num_heads
        counts['A']['T'] += weight_A*num_tails
        counts['B']['H'] += weight_B*num_heads
        counts['B']['T'] += weight_B*num_tails

    # M setp
    new_theta_A = counts['A']['H']/(counts['A']['H']+counts['A']['T'])
    new_theta_B = counts['B']['H']/(counts['B']['H']+counts['B']['T'])

    return [new_theta_A, new_theta_B]

def em_single(priors,observations):

"""

performs a single Em step

Arguments

---------

priors:[theta_A,theta_B]

observations:[m X n matrix]

Returns

-------

new_priors:[new_theta_A,new_theta_B]

"""

counts ={'A':{'H':0,'T':0},'B':{'H':0,'T':0}}

theta_A = priors[0]

theta_B = priors[1]

# E setp

for observation in observations:

len_observation = len(observation)

# 对数组求和 head =1，tail =0

num_heads = observation.sum()

num_tails = len_observation - num_heads

# 如果属于A类，A的分布概率和属于B类的分布概率

contribution_A = stats.binom.pmf(num_heads,len_observation,theta_A)

contribution_B = stats.binom.pmf(num_heads,len_observation,theta_B)

# z分布概率

weight_A = contribution_A /(contribution_A+contribution_B)

weight_B = contribution_B /(contribution_A+contribution_B)

# Incrementing counts

counts['A']['H'] += weight_A*num_heads

counts['A']['T'] += weight_A*num_tails

counts['B']['H'] += weight_B*num_heads

counts['B']['T'] += weight_B*num_tails

# M setp

new_theta_A = counts['A']['H']/(counts['A']['H']+counts['A']['T'])

new_theta_B = counts['B']['H']/(counts['B']['H']+counts['B']['T'])

return [new_theta_A, new_theta_B]

（3）迭代一次输出结果为：

em_single([0.6,0.5],observations)

1	em_single([0.6,0.5],observations)

运行结果为：[0.71301223540051617, 0.58133930831366265]

4.6.2.7.5 EM主循环

给定循环的两个终止条件：模型参数变化小于阈值；循环达到最大次数，就可以写出EM算法的主循环了。

def em(observations,prior,tol=1e-6,iterations=1000):
    import math
    iteration = 0
    while iteration

def em(observations,prior,tol=1e-6,iterations=1000):

import math

iteration = 0

while iteration

最终结果为：

em(observations, [0.6,0.5])

1	em(observations, [0.6,0.5])

运行结果为：
[[0.79678875938310978, 0.51958393567528027], 14]
我们可以改变初值，试验初值对EM算法的影响。

em(observations, [0.9,0.2])

1	em(observations, [0.9,0.2])

运行结果为：
[[0.79678843908109542, 0.51957953211429142], 11]
EM算法对于参数的改变还是有一定的健壮性的。

最终实习生b的EM算法得出的结果，跟实习生a得出的参数还是非常相近的，但EM算法跟初始值的设置有着很大的关系，不信，修改[06,0.5]多尝试尝试。

em(observations, [0.5,0.6])

1	em(observations, [0.5,0.6])

运行结果为：
[[0.51958345063012845, 0.79678895444393927], 15]

参考：
http://blog.csdn.net/u014688145/article/details/53073266
http://blog.csdn.net/zouxy09/article/details/8537620
http://blog.csdn.net/lilynothing/article/details/64443563

Python技术交流与分享

分享技术平台