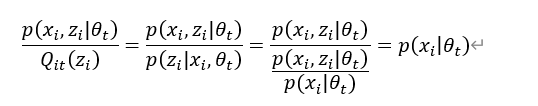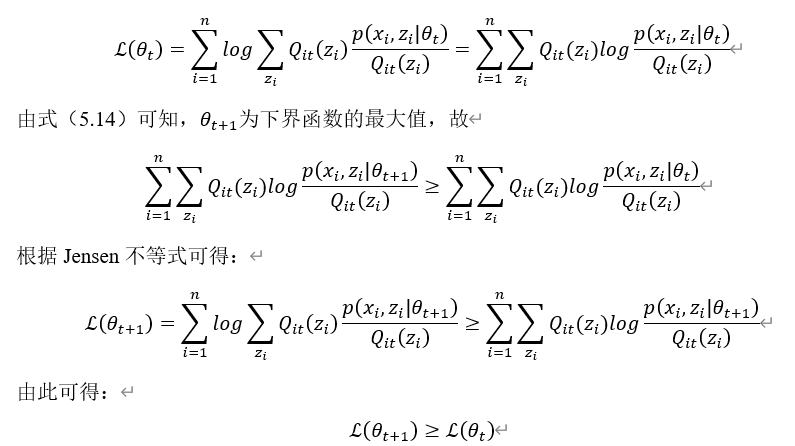有关AIGC的三个问题
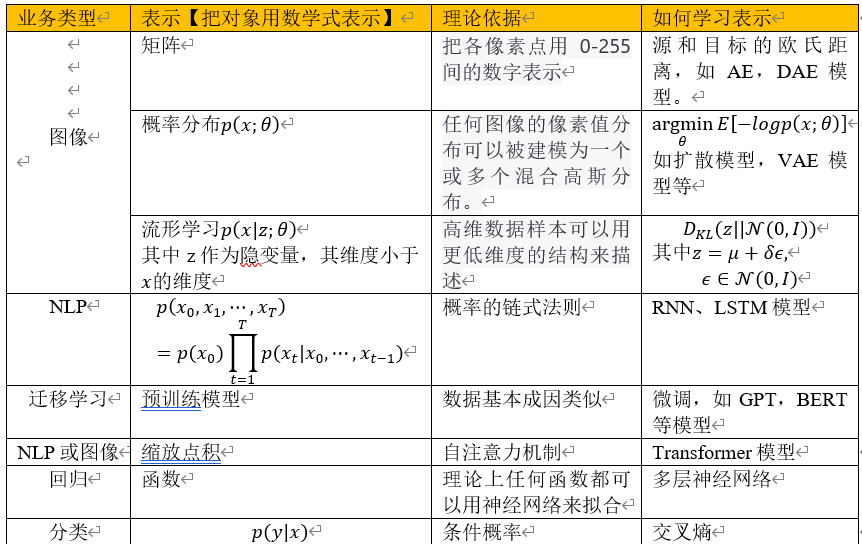
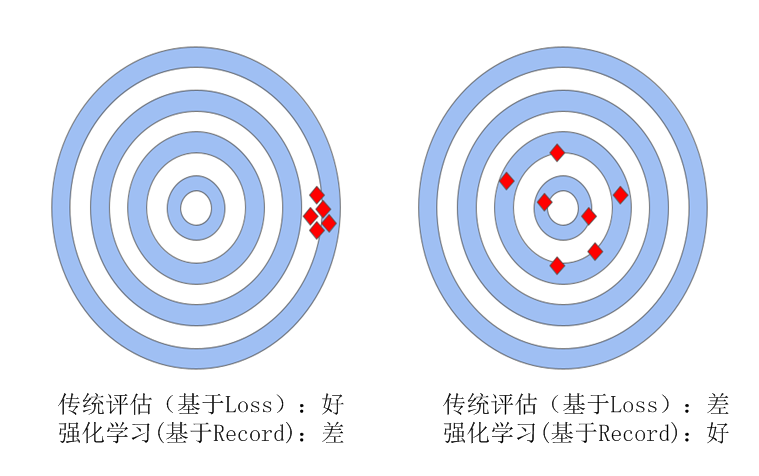
1.如何科学表示机器学习的目标?什么样表示效率更高?如何学习表示?
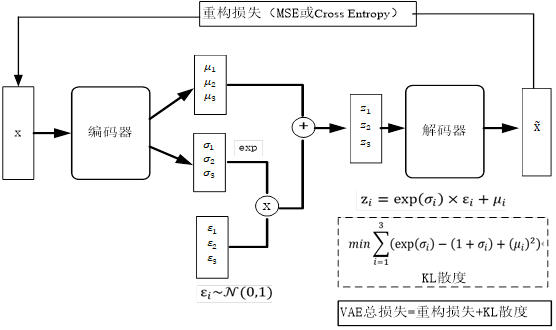
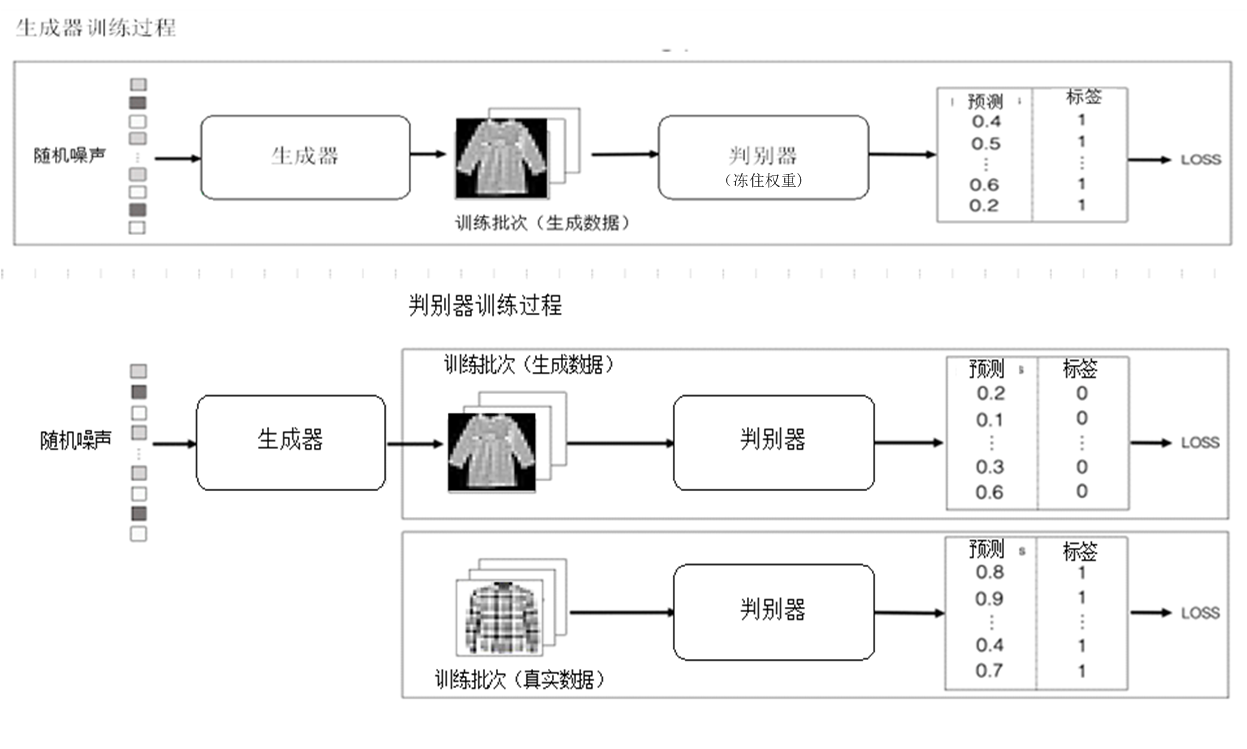
2.生成模型大都采样编码器-解码器的架构(如AE,VAE,Transformer、Diffusion等等),其优势和不足是什么?
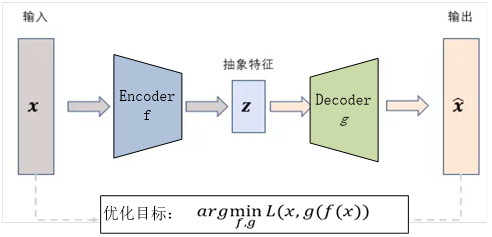
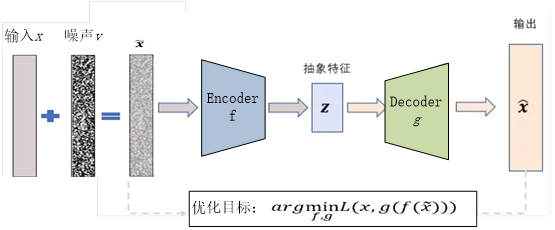
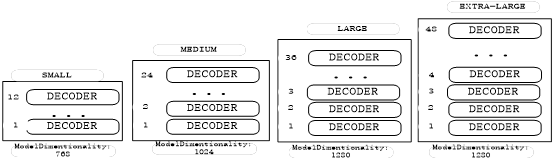
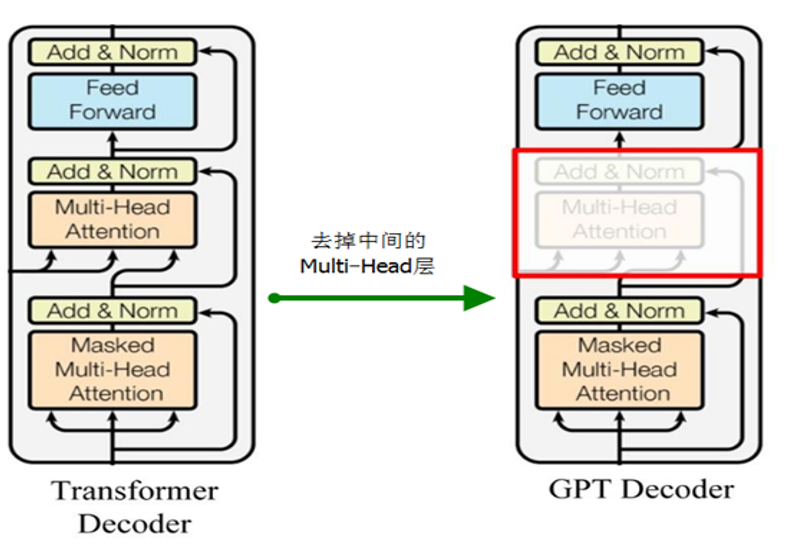
编码器-解码器架构(Encoder-Decoder Architecture)在生成模型中得到了广泛的应用,尤其在自然语言处理(NLP)和序列到序列(Seq2Seq)任务中。这种架构通常由两部分组成:编码器负责将输入序列编码成固定大小的向量,解码器则负责根据这个向量生成输出序列。
(1)优势:
•通用性强:
编码器-解码器架构能够处理不同长度的输入和输出序列,使其在各种序列生成任务中都具有通用性。
•结构灵活:
编码器和解码器可以使用不同的神经网络结构来实现,如循环神经网络(RNN)、长短期记忆网络(LSTM)或Transformer等,这使得该架构能够根据具体任务需求进行定制和优化。
•捕捉序列依赖关系:
编码器能够捕捉输入序列中的依赖关系,并将其编码成固定大小的向量,而解码器则能够利用这个向量生成具有依赖关系的输出序列。编码器-解码器结构通常能够很好地重建输入数据,有利于学习数据的表示形式。
•可解释性强:
编码器产生的潜在表示通常可以用于解释模型的决策过程。
(2)不足:
•信息损失:
将整个输入序列编码成固定大小的向量可能会导致信息损失,特别是当输入序列较长或包含复杂结构时。这种信息损失可能会影响解码器生成准确输出的能力。
•长序列生成问题:
在解码过程中,随着生成序列长度的增加,错误可能会逐渐累积,导致生成的序列质量下降。这尤其是在使用RNN或LSTM等结构时更为明显。
•缺乏并行性:
在训练过程中,编码器和解码器通常需要依次处理输入和输出序列,这使得模型训练难以并行化,从而限制了训练速度的提升。
为了克服这些不足,研究者们提出了一系列改进方法,如注意力机制(Attention Mechanism)、Transformer模型等。这些方法在一定程度上提高了编码器-解码器架构的性能和效率,使其在各种生成任务中取得了更好的表现。
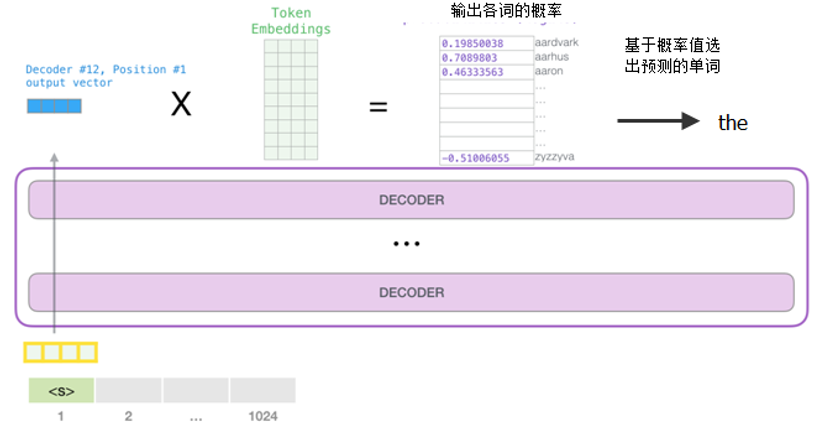
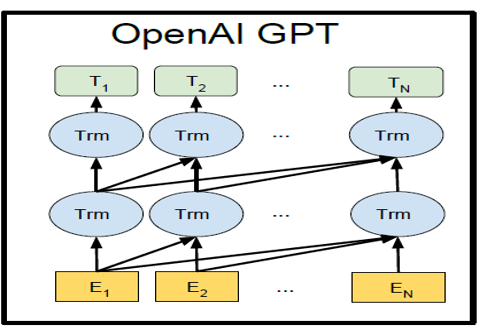
3.Transformer模型具有涌现潜力的几个关键技术是什么?
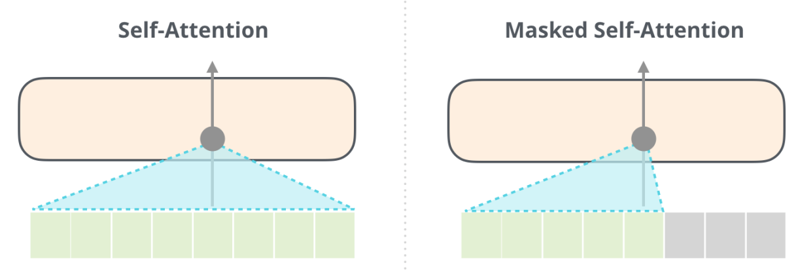
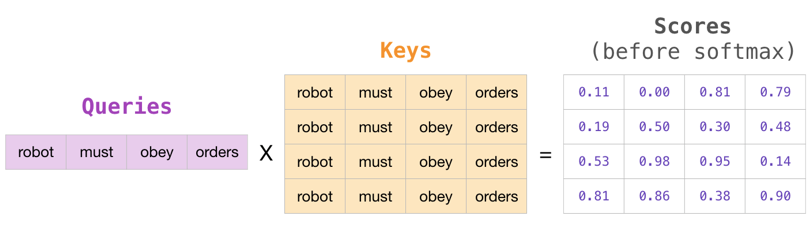
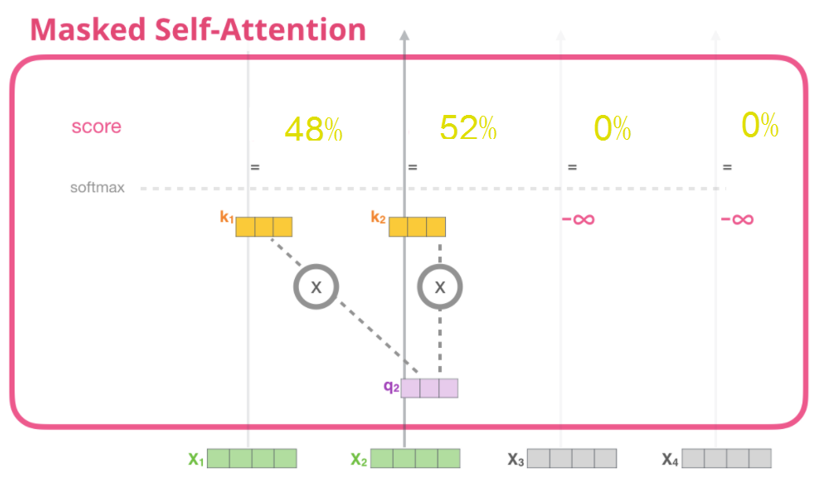
•自注意力机制(Self-Attention):
Transformer 中的自注意力机制使模型能够在不同位置之间建立关联,即同时考虑输入序列中不同位置的信息,有效地捕捉长距离依赖关系。
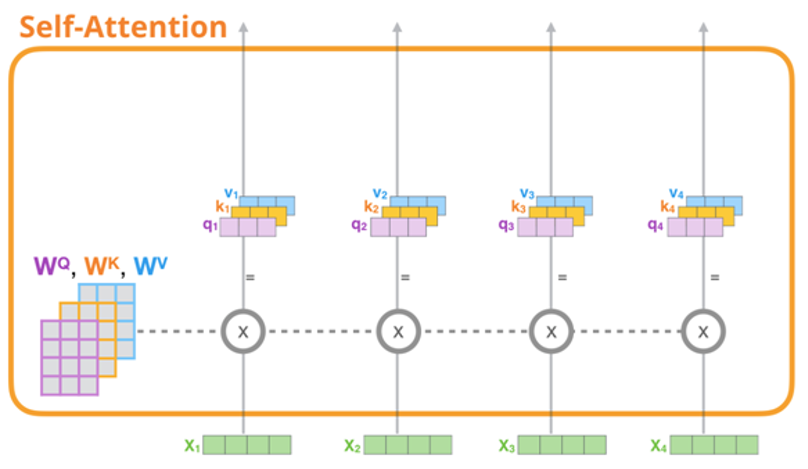
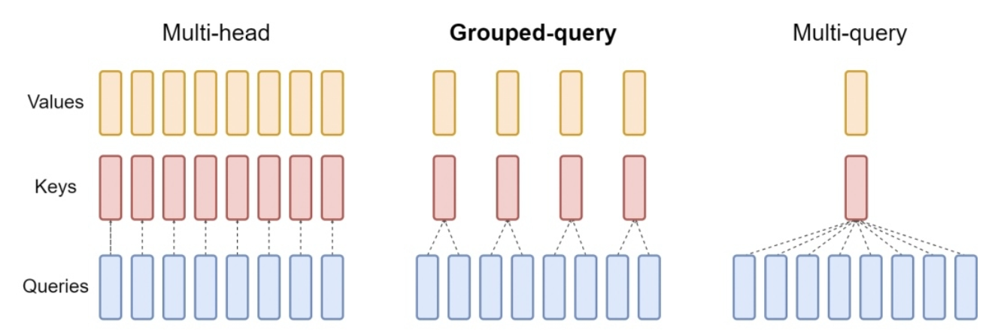
•多头自注意力机制:
这是Transformer模型的核心技术之一。该机制通过多个不同的注意力头,从不同的角度对输入序列进行关注,从而得到对输入序列的抽象表示。每个注意力头都由一个线性变换和一个点积注意力机制组成。这种机制有助于模型在不同位置捕获重要的信息,并且能够自动地捕捉输入序列中的长距离依赖关系。通过将多个注意力头的结果拼接起来,可以得到一个高维的表示向量,该向量可以被用于生成解码器的输出序列。
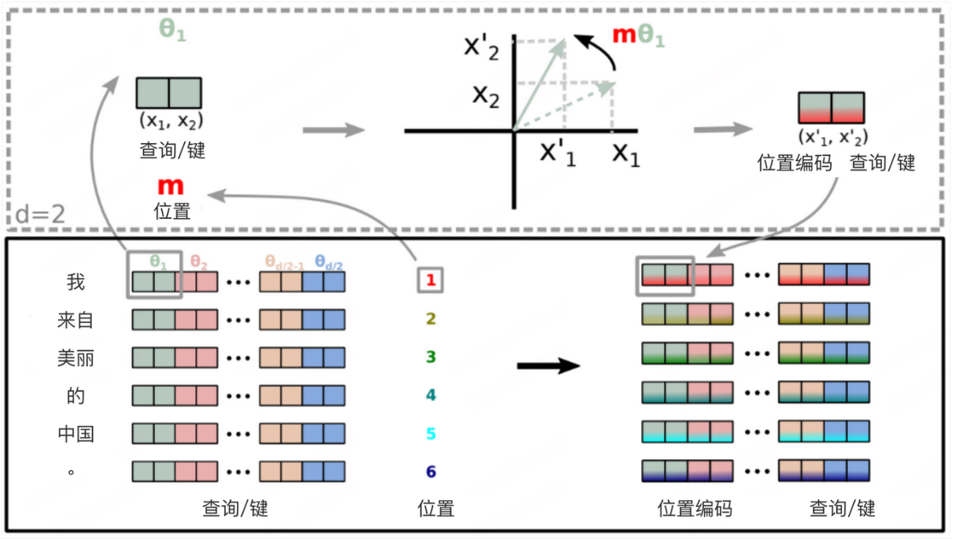
•位置编码:
由于Transformer模型没有明确的语法结构,无法像传统的语言模型那样利用上下文信息来预测当前词。为了解决这个问题,Transformer模型引入了位置编码,将每个单词在序列中的位置信息编码为一种特殊的向量。这种编码有助于模型更好地理解输入序列中的词语顺序和语义信息,从而使得模型可以更好地处理序列数据。
•残差连接和层归一化:
为了缓解深度神经网络中的梯度消失问题,Transformer模型在每个层之后添加了残差连接。此外,层归一化也可以帮助模型更好地学习和泛化。这些技术有效地提高了模型的长期记忆能力,使得模型在处理长序列时能够保留更多的上下文信息。
•基于自回归训练(Autoregressive Training)和无监督预训练(Unsupervised Pre-training):
Transformer 模型通常通过自回归训练或无监督预训练方法进行训练,有助于提升模型的泛化能力和性能。
这些关键技术共同构成了 Transformer 模型的核心思想和成功之处,使其在自然语言处理领域获得了革命性的突破,并在其他序列建模任务中展现了强大的潜力。












![T_i=[C*i]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_804a84d357dd8e2a67e038c9763eb063.gif)
![T_i=[C*i^2]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_fc23122d22fd48c921cd0d431ddda821.gif)







 构
构