6.3 PCA
6.3.1概述
主成分分析方法 (Principal Component Analysis,简称PCA)是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴,大部分方差都包含在前面k个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。事实上,这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,从而实现对数据特征的降维处理。
总之,主成分分析算法的主要目标就是使在新坐标系投影后,各特征的方差最大化,特征之间最小化或为0。如果把各特征进行去中心化之后, 对称矩阵对角线上的值正好是个特征的方差,其它值为协方差。
对称矩阵对角线上的值正好是个特征的方差,其它值为协方差。
如何实现上述目标?级找到一个变换使之变换后的方差最大?根据特征值分解可知,对称矩阵 实现对角化,对角化上的特征值代表
实现对角化,对角化上的特征值代表 的信息量,对这些特征值进行排序后,就可获取较大一些特征值,而我们要找的这个变换就是由对称矩阵
的信息量,对这些特征值进行排序后,就可获取较大一些特征值,而我们要找的这个变换就是由对称矩阵 的特征向量构成的式(6.2)中矩阵Q。
的特征向量构成的式(6.2)中矩阵Q。
6.3.2基于特征值分解协方差矩阵实现PCA算法
输入:数据集![X=[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_193e348a7f28c1809cf3be796d9e2409.gif) ,需要降到k维。
,需要降到k维。
1) 去平均值(即去中心化),即每一位特征减去各自的平均值。这种处理方式不会改变样本的相对分布,其效果就像坐标轴进行了移动。
2) 计算协方差矩阵 ,注:这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。
,注:这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。
3) 用特征值分解方法求协方差矩阵 的特征值与特征向量。
的特征值与特征向量。
4) 对特征值从大到小排序,选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵Q。
5) 将数据转换到k个特征向量构建的新空间中,即Y=QX
例1:设 使用PCA方法进行降维。
使用PCA方法进行降维。
解:
(1)去中心化
对每个特征(这里是x行、y行)去中心化,计算的每个特征的均值都是0.
(2) 计算协方差矩阵
(4)把数据转换到k个特征向量构建的新空间中
这里我们取Q中第1行 乘以原数据得到:
乘以原数据得到: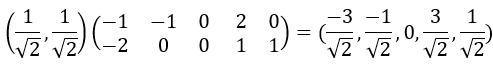
这个变换把原来不一条直线上的5个点,映射到一条直线上,即把2维变为1维,这个变换过程可用下图直观表示:
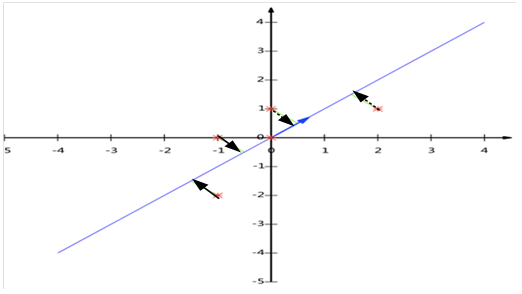
新生成的坐标
 就是原来的5个坐标在单位向量
就是原来的5个坐标在单位向量 上的投影。
上的投影。
6.3.3基于SVD分解协方差矩阵实现PCA算法
当矩阵X维度较大时,计算协方差矩阵 还是比较耗资源,这种情况下是否有更好的方法呢?针对这种情况,我们知道SVD中U(即左奇异矩阵)就是由
还是比较耗资源,这种情况下是否有更好的方法呢?针对这种情况,我们知道SVD中U(即左奇异矩阵)就是由 的特征向量构成的,为此,我们可以使用SVD的方法求协方差矩阵的特征值和特征向量,其它步骤与用特征值方法类似,具体步骤如下:
的特征向量构成的,为此,我们可以使用SVD的方法求协方差矩阵的特征值和特征向量,其它步骤与用特征值方法类似,具体步骤如下:
输入:数据集![X=[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_193e348a7f28c1809cf3be796d9e2409.gif) ,需要降到k维。
,需要降到k维。
1) 去平均值,即每一位特征减去各自的平均值。
2) 计算协方差矩阵。
3) 通过SVD计算协方差矩阵的特征值与特征向量。实际上,PCA仅仅使用了我们SVD的左奇异矩阵。
4) 对特征值从大到小排序,选择其中最大的k个。然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
5) 将数据转换到k个特征向量构建的新空间中。
例2:用SVD方法解例1.
为方便起见,这里我们使用Python来实现这个过程。
|
1 2 3 4 5 6 7 8 |
import numpy as np X=np.array([[-1,-1,0,2,0.],[-2.,0,0.,1,1.]]) U,d,V = np.linalg.svd(X, full_matrices=True) print('X:',X) print('U:',U) U1=U[0,:] print('U1:',U1) np.dot(U1,X) |
运行结果:
X: [[-1. -1. 0. 2. 0.]
[-2. 0. 0. 1. 1.]]
U: [[-0.70710678 -0.70710678]
[-0.70710678 0.70710678]]
U1: [-0.70710678 -0.70710678
Out[23]:
array([2.12132034,0.70710678,0.,-2.12132034,-0.70710678])
这里相当于使用基向量 与X进行内积,得到结果为:
与X进行内积,得到结果为:
array([2.12132034,0.70710678,0.,-2.12132034,-0.70710678])
如果把小数用平方根表示这个结果就是:

X与基向量 的映射关系如下图所示。与例1相比,只是新轴的方向相反而已。
的映射关系如下图所示。与例1相比,只是新轴的方向相反而已。
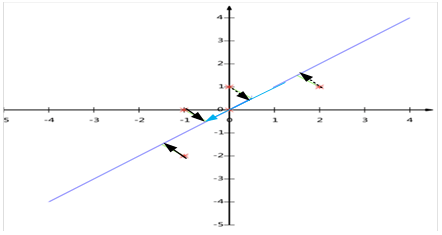
从例1和例2来看,这两种方法可谓异曲同工!
【注意】
左奇异矩阵可以用于对行数的压缩;右奇异矩阵可以用于对列(即特征维度)的压缩。我们用SVD分解协方差矩阵实现PCA可以得到两个方向的PCA降维(即行和列两个方向)。