3.2离散型随机变量及分布
如果随机变量X的取值是有限的或者是可数无穷尽的值,如:

则称 X为离散随机变量。
3.2.1 离散型随机变量及分布概述
设 是随机变量X的所有可能取值,对每个取值
是随机变量X的所有可能取值,对每个取值 是其样本空间S上的一个事件,为描述随机变量X,还需知道这些事件发生的可能性(概率)。
是其样本空间S上的一个事件,为描述随机变量X,还需知道这些事件发生的可能性(概率)。
设离散型随机变量X的所有可能取值为 。
。

称之为X的概率分布或分布律,也称概率函数。
常用表格形式来表示X的概率分布:
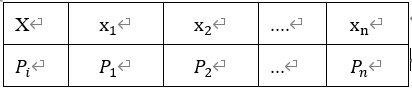
由概率的定义, 必然满足:
必然满足:
(1) 
(2) 
例1:某篮球运动员投中篮圈的概率是0.8,求他两次独立投篮投中次数X的概率分布。
解 X可取0,1,2为值,记 ={第i次投中篮圈},i=1,2,则
={第i次投中篮圈},i=1,2,则
由此不难得到下列各情况的概率:
投了两次没一次投中,即:

投了两次只投中一次,即:

投了两次两次都投中,即:

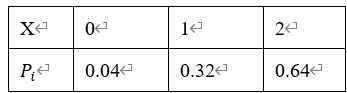
且

于是随机变量X的概率分布可表示为:
若已知一个离散型随机变量X的概率分布:

则由概率的可列可加性,可得随机变量X的累加值为:

例如,设X的概率分布由例1给出,则

3.2.2 伯努利分布
伯努利分布又称为二点分布或0-1分布,服从伯努利分布的随机变量X取值为0或1两种情况,且它的分布列为P(X=1)=p,P(X = 0) = l − P其中(0 < P < 1),则称X服从参数为p的伯努利分布,记作 。其概率函数可统一写成:
。其概率函数可统一写成:

其中
X服从伯努利分布,记为
随机变量X的期望:
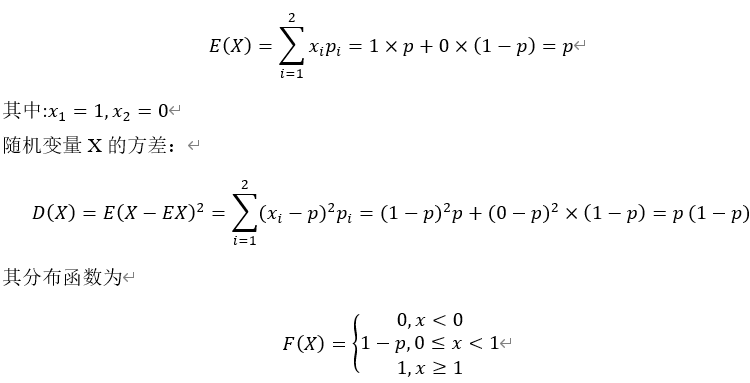
当 时,伯努利分布为离散型平均分布。
时,伯努利分布为离散型平均分布。
伯努利分布在机器学习中经常看到,如逻辑回归模型拟合的就是这种模型。
3.2.3二项分布
二项分布是重要的离散概率分布之一,由瑞士数学家雅各布·伯努利(Jokab Bernoulli)提出。一般用二项分布来计算概率的前提是,每次抽出样品后再放回去,并且只能有两种试验结果,比如黑球或红球,正品或次品等。二项分布指出,假设某样品在随机一次试验出现的概率为p,那么在n次试验中出现k次的概率为:

假设随机变量X满足二项分布,且知道n,p,k等参数,我们如何求出各种情况的概率值呢?方法比较多,这里介绍一种比较简单的方法,利用scipy库的统计接口stats即可,具体如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import numpy as np import matplotlib.pyplot as plt import math from scipy import stats %matplotlib inline n = 20 p = 0.3 k = np.arange(0,41) #定义二项分布 binomial = stats.binom.pmf(k,n,p) #二项分布可视化 plt.plot(k, binomial, 'o-') plt.title('binomial:n=%i,p=%.2f'%(n,p),fontsize=15) plt.xlabel('number of success') plt.ylabel('probalility of success', fontsize=15) plt.grid(True) plt.show() |
运行后的二项分布图如图3-2所示。
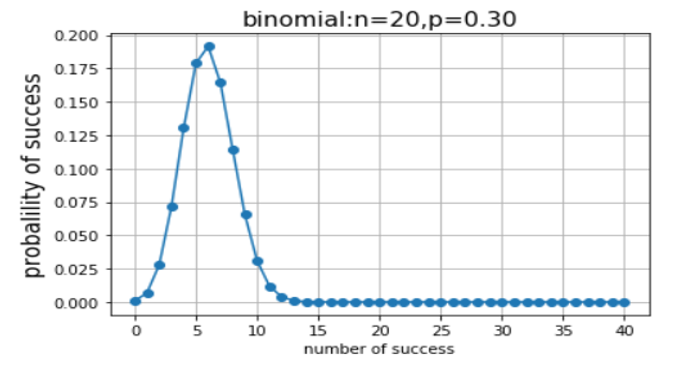
图3-2 二项分布图
3.2.4多项分布
多项分布是伯努利分布的推广,假设随机向量X的取值有k种情况,即可表示为:  ,则有:
,则有:

随机变量X有k种情况,在实际使用时,往往把k种情况用度热编码来表示,如X=1,可表示为![[1,0,0,\cdots,0],X=2,](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_03c5f484dd0681c3f5deb663acbf8bdd.gif) 可表示为
可表示为![[0,1,0,0,\cdots,0]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_d3dbda39c04813c72bdd58877d226db0.gif) 。这里用
。这里用![[y_1,y_2,\cdots,y_k]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_494bfb791bf3f49062e568e7e20f286e.gif) 表示独热编码。
表示独热编码。
这样多项分布可表示为:

多项分布在机器学习中应用非常广泛,如softmax回归模拟的就是多项分布,神经网络多分类的模型也是拟合多项分布。
3.2.5泊松(Poisson)分布
若随机变量X所有可能取值为 ,它取各个值的概率为:
,它取各个值的概率为:

这里介绍了离散型随机变量的分布情况,如果X是连续型随机变量,其分布函数通常通过密度函数来描述,具体请看下一节。