第1章 一元函数微积分
一元函数是微积分的核心内容,微积分为研究函数性质提供了理论和方法,在机器学习中被广泛使用,尤其在寻找函数极值方面。
1.1 导数的定义
导数定义为函数f(x)的自变量变化趋于0时,函数值的变化量与自变量变化量比值的极限,函数y=f(x)在x点处的导数定义为:

如果式(5.1)的极限存在,则称函数f(x)在x点处可导。
例1 当f(x)=3x时,

例2  时,
时,

已知函数f(x),求导函数 ,称为对函数f(x)求导。当式(5.1)的极限存在时,称函数可导。导函数的含义如图5-1所示。作出函数f(x)的图像,
,称为对函数f(x)求导。当式(5.1)的极限存在时,称函数可导。导函数的含义如图5-1所示。作出函数f(x)的图像,  表示图像切线的斜率。
表示图像切线的斜率。
图5-1 导数的含义, 表示切线PQ的斜率。
表示切线PQ的斜率。

式(5.1)的极限也可写成如下形式:

式(5.1)与式(5.2)是等价的。
函数y=f(x)在x点处的导数除用f^' (x)表示之外,以下表达式是等价的。

其中 和D是微分运算符,表示微分操作。常见函数的微分有:
和D是微分运算符,表示微分操作。常见函数的微分有:
Dc=0(c是一个常数)
 (a是任意实数)
(a是任意实数)


Dsinx=conx
Dconx=-sinx
基本函数的求导公式:
幂函数:
指数函数:


三角函数:




对数函数:


1.2 导数的四则运算
1)加法

2)减法

3)乘法


4)除法

5)倒数

1.3 复合函数的导数
假设
则复合函数 的导数为:
的导数为:

或写成如下:

这称为链式法则,这个公式可以推广到多元函数。
例 3: 求 的导数
的导数
该函数是 与
与 的复合函数,其导数为
的复合函数,其导数为

练习:
1.求函数 的导数。
的导数。
2.求函数 的导数。
的导数。
3.求函数 的导数,该函数也称为sigmoid函数。
的导数,该函数也称为sigmoid函数。
1.4 高阶导数
对导数继续求导可以得到高阶导数,如二阶导数是一阶导数的导数,表示为:
 或
或
例如:求函数 的二阶导数
的二阶导数
其一阶导数为:
其二阶导数为: 
1.5 导数与极值点
函数导数与极值点有一定关系,费马定理说明了两者的关系,费马定理的具体内容为:
假设函数 在点
在点 点可导,如果在
点可导,如果在 点处取得极值,则必定有:
点处取得极值,则必定有:

费马定理给出了可导函数取极值的一阶必要条件,导数为0的点又称为函数的驻点。
【注意】导数为0是函数取极值的必要条件,而不是充分条件。即
 是
是 的极值点。
的极值点。
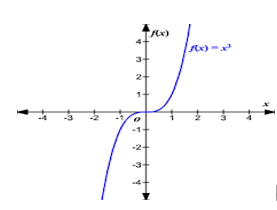
例如, ,在x=0处的导数为0,但x=0不是函数f(x)的极值点,如下图所示:
,在x=0处的导数为0,但x=0不是函数f(x)的极值点,如下图所示:
函数 的图形
的图形
不过我们通常通过求函数的驻点来寻找函数的候选极值点。在SVM算法中使用。
如果函数 在点
在点 处导数等于0,是否存在
处导数等于0,是否存在 为极值点的充分条件呢?当然有:
为极值点的充分条件呢?当然有:
(1)通过判断点 ,左右侧导数来确定是极大还是极小值;
,左右侧导数来确定是极大还是极小值;
(2)如果函数 存在二阶导数,则可通过在点
存在二阶导数,则可通过在点 二阶导数大于0还是小于0来判断;
二阶导数大于0还是小于0来判断;
(3)如果函数 为凸(或凹)函数,则驻点就是极值点。
为凸(或凹)函数,则驻点就是极值点。
1.6 导数与中值定理
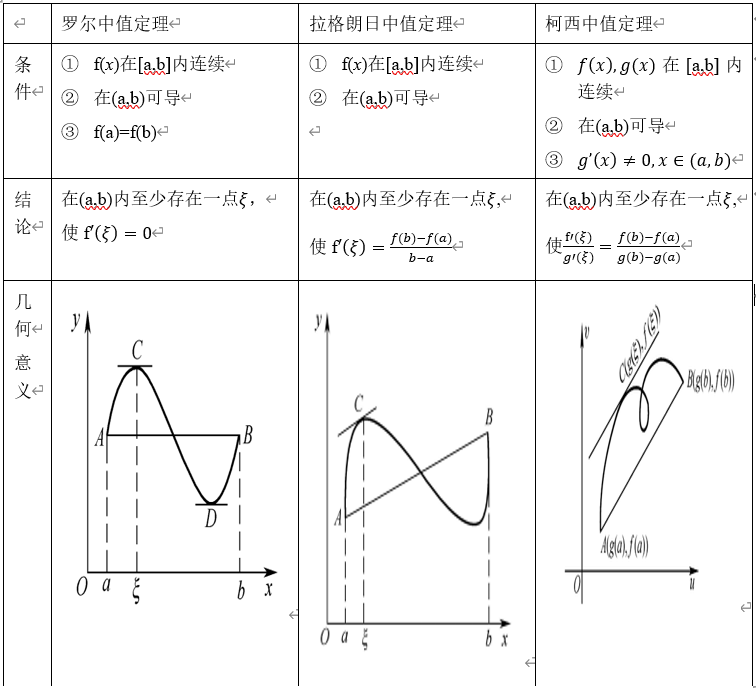
微分中值定理建立了导数与函数值之间的关系,是导数应用的基础,在微积分理论中占有重要地位,本节将介绍 3 个中值定理,先介绍罗尔定理,然后再由它推出拉格朗日中值定理、柯西中值定理。
1、中值定理概览
2、简单证明
(1)证明罗尔中值定理:
基本思路:根据费马定理,要证明函数f(x)在某点导数为0,如果能说明这点为极值即可。如果f(x)在[a,b]为常数,则在该区域内,导数处处为0;如果函数f(x)不为常数,因f(x)在[a,b]上连续,故其在[a,b]上必定存在极值点,因f(a)=f(b),所以,这个极值点,不在端点a或b上,即在(a,b)至少存在一点 ,为函数f(x)的极值点,根据费马定理可得,该点的导数必为0,即有:
,为函数f(x)的极值点,根据费马定理可得,该点的导数必为0,即有:
(2)拉格朗日中值定理
罗尔中值定理中条件f(a)=f(b)比较严苛,拉格朗日中值定理去掉这个条件,不过通过构造一个辅助函数,在利用罗尔中值定理可证明拉格朗日中值定理。
该辅助函数为:
可以证明g(a)=g(b),然后利用罗尔中值定理即可证明。
(3)柯西中值定理
通过构造一个辅助函数,再利用罗尔中值定理便可证明,该辅助函数为:

可以证明F(a)=F(b),然后再利用罗尔中值定理便可证明。
3、实例
例1:证明当 证明: 设f(t)=ln(t+1),显然f(t) 在[0,x]上满足拉格朗日中值定理,故在(0,x)中至少存在一点
证明: 设f(t)=ln(t+1),显然f(t) 在[0,x]上满足拉格朗日中值定理,故在(0,x)中至少存在一点 使得下式成立:
使得下式成立:  代入f(t)=ln(t+1)得:
代入f(t)=ln(t+1)得: 因
因 ,故有:
,故有: ,从而
,从而
1.7 导数与函数的单调性
函数导数与函数的单调性有密切关系,当然需要满足一定条件。
定理;假设函数f(x) 在[a,b]连续,在(a,b)上可导,则有:
(1)如果在(a.b)内 时,那么函数
时,那么函数 在[a,b]内单调递增;
在[a,b]内单调递增;
(2)如果在(a.b)内 时,那么函数f(x)在[a,b]内单调递减。
时,那么函数f(x)在[a,b]内单调递减。
证明:利用拉格朗日中值定理可以证明。
在[a,b]上,任取两点 ,由拉格朗日中值定理可得: 在
,由拉格朗日中值定理可得: 在 内,至少存在一点
内,至少存在一点 ,使得下式成立:
,使得下式成立:  这里
这里 从而可得:
从而可得: ,即函数f(x)在[a,b]单调递增
,即函数f(x)在[a,b]单调递增
同理可证明在(a,b)内 时,函数f(x)在[a,b]内单调递减。 例1:证明当
时,函数f(x)在[a,b]内单调递减。 例1:证明当 时,
时,
证明:令

当 时,
时, ,函数单调递减,所以
,函数单调递减,所以
当 时,
时, ,函数单调递增,所以
,函数单调递增,所以
所以,当 时,
时, ,即:
,即:
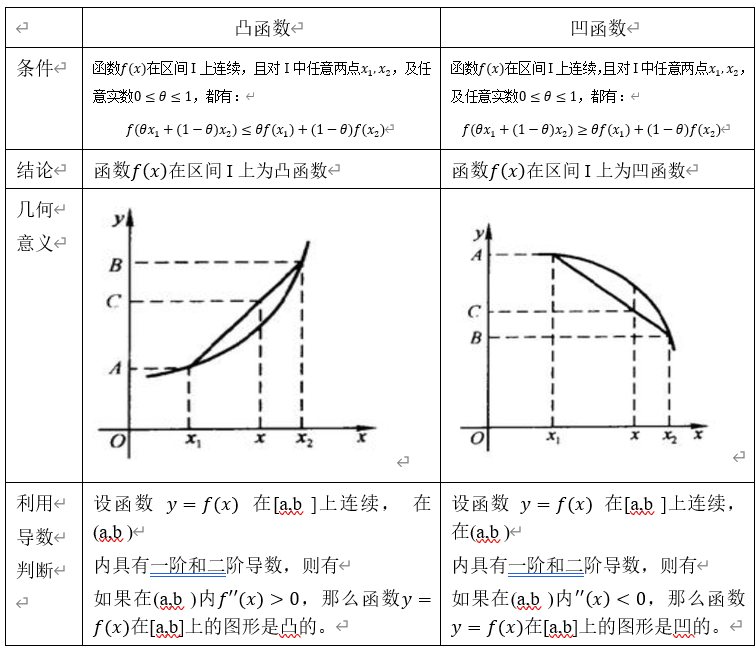
1.8 导数与函数的凹凸性
函数的单调性反映在图形上就是曲线的上升或下降,但上升或下降过程中还
要考虑曲线的弯曲方向,如下图所示:
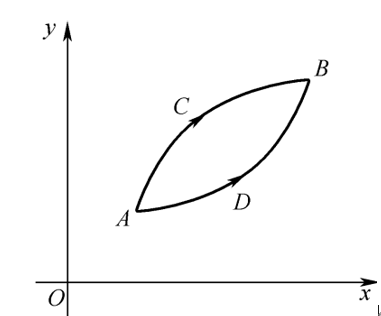
两条弧线都是上升的,但ADB 是凸的曲线弧,而ACB 是凹的曲线弧,即两者凹凸性不同.下面来讨论曲线的凹凸性及其判定方法.曲线的凹凸性可以用连接曲线弧上任意两点的弦的点与弧线上弦的点具有相同横坐标的点的位置关系来描述,我们有如下定义:
【说明】这里的定义以机器学习中命名为准,国内高中的凹凸定义可能与之相反。
例1,判断曲线 的凹凸性
的凹凸性
解:该曲线的图像为:
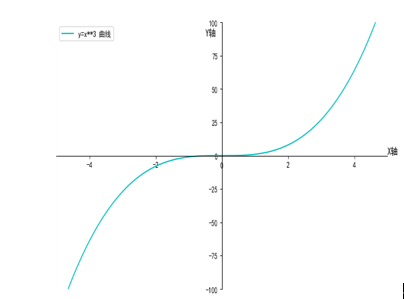
当x>0时, ,y为凸函数
,y为凸函数
当x<0时, ,y为凹函数
,y为凹函数
【注意】这里函数y=x**3的凹凸性在点(0,0)处发生改变,我们称这样的点为拐点。
拐点的定义:
设y=f(x)在区间I上连续, 是I内的点.如果曲线y=f(x)在经过点
是I内的点.如果曲线y=f(x)在经过点 时,曲线的凹凸性(或函数二阶导的符号)改变了,那么就称点
时,曲线的凹凸性(或函数二阶导的符号)改变了,那么就称点 为这曲线的拐点(反曲点)。需要明确的是:拐点是曲线上的一点,它由横坐标和纵坐标构成,不要只把横坐标当成拐点。
为这曲线的拐点(反曲点)。需要明确的是:拐点是曲线上的一点,它由横坐标和纵坐标构成,不要只把横坐标当成拐点。
 的
的 领域内有定义,如果对去心领域内任何一点x都有
领域内有定义,如果对去心领域内任何一点x都有 (或
(或 ,则称
,则称 是函数f(x)的极小值,或为极大值。
是函数f(x)的极小值,或为极大值。 连续,在点
连续,在点 的某去心领域可导。
的某去心领域可导。 则函数f(x)在点
则函数f(x)在点 处取得极小值;
处取得极小值; 则函数f(x)在点
则函数f(x)在点 处取得极大值;
处取得极大值; 符合保持不变,则函数f(x)在点
符合保持不变,则函数f(x)在点 处没有极值。
处没有极值。 处二阶可导,且
处二阶可导,且 为驻点(即
为驻点(即 。
。 则函数f(x)在点
则函数f(x)在点 处取得极大值; 如
处取得极大值; 如 则函数f(x)在点
则函数f(x)在点 处取得极小值;
处取得极小值; 则函数f(x)在点
则函数f(x)在点 不一定取得极值,需进一步分析。
不一定取得极值,需进一步分析。