第6章 模型评估与模型优化
6.1模型评估一般方法
对模型的性能或优劣进行评估，通过评价指标来衡量。模型评估是机器学习任务中非常重要的一环。不同的机器学习任务有着不同的评价指标，同时同一种机器学习任务也有着不同的评价指标，每个指标的着重点不一样。如分类（classification）、回归（regression）、聚类（clustering）、SVM、推荐（recommendation）等。并且很多指标可以对多种不同的机器学习模型进行评价，如精确率－召回率（precision-recall），可以用在分类、推荐等。像分类、回归、SVM都是监督式机器学习，本节的重点便是监督式机器学习的一些评价指标。
在实际情况中，我们会用不同的度量去评估我们的模型，而度量的选择，完全取决于模型的类型和模型以后要做的事。下面我们就会学习到一些用于评价模型的常用度量和图表以及它们各自的使用场景。
6.1.1分类评价指标
分类是指对给定的数据记录预测该记录所属的类别。并且类别空间已知。它包括二分类与多分类，二分类便是指只有两种类别，其输出不是0就是1；或是与否等，也可以称为“负”（negative）与正（positive）两种类别，一般在实际计算中，将其映射到“0”-“1” class中；而多分类则指类别数超过两种。下面主要根据二分类的评价指标进行讲解，不过同时它们也可扩展到多分类任务中。下面对分类中一些常用的评价指标进行介绍。
1)混淆矩阵（Confusion Matrix）
混淆矩阵显示了分类模型相对数据的真实输出（目标值）的正确预测和不正确预测数目。矩阵为NxN，其中N为目标值（类）数目。这类模型的性能通常使用矩阵中的数据评估。下表为两个类别（阳性和阴性）的2x2混淆矩阵。
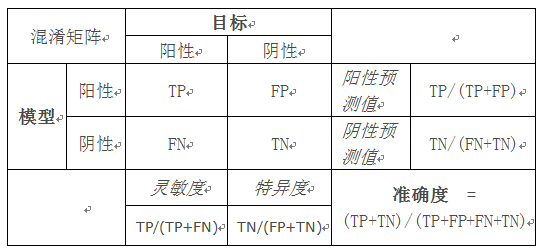
常用术语：
阳性 (P, positive)
阴性 (N, Negative)
真阳性 (TP, true positive)：正确的肯定。又称：命中 (hit)
真阴性 (TN, true negative)：正确的否定。又称：正确拒绝 (correct rejection)
伪阳性 (FP, false positive)：错误的肯定，又称：假警报 (false alarm)、第二型错误
伪阴性 (FN, false negative)：错误的否定，又称：未命中(miss)、第一型错误
灵敏度(sensitivity)或真阳性率(TPR, true positive rate)：sensitivity = TP/(TP + FN);
灵敏度又称为召回率(Recall)=TP/(TP+FN) = 1 - FN/P
特异性（真阴性率）specificity = TN /（FP + TN）
准确度 (ACC, accuracy）：ACC = (TP + TN) / (P + N)
预测正确的数占样本数的比例。
F1评分：
精度和灵敏度的调和平均数。
F1 = 2 precision * recall / (precision+recall) = 2TP/(2TP+FP+FN)
示例:
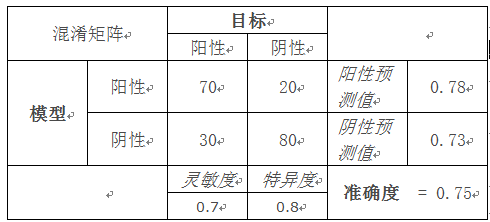
混淆矩阵 目标
阳性 阴性
模型 阳性 70 20 阳性预测值 0.78
阴性 30 80 阴性预测值 0.73
灵敏度 特异度 准确度 = 0.75
0.7 0.8
2)ROC曲线
判定方法：ROC曲线应尽量偏离参考线。
原理：ROC全称为Receiver Operation Characteristic Curve,ROC曲线其实就是从混淆矩阵衍生出来的图形，其横坐标为1-Specificity,纵坐标为Sensitivity。
上面那条曲线就是ROC曲线，随着阈值的减小，更多的值归于正类，敏感度和1-特异度也相应增加，所以ROC曲线呈递增趋势。而那条45度线是一条参照线，也就是说ROC曲线要与这条曲线比较。
简单的说，如果我们不用模型，直接随机把客户分类，我们得到的曲线就是那条参照线，然而我们使用了模型进行预测，就应该比随机的要好，所以ROC曲线要尽量远离参照线，越远，我们的模型预测效果越好。
3)AUC（ROC曲线下面积）
判定方法：AUC应该大于0.5.
原理：ROC曲线是根据与那条参照线进行比较来判断模型的好坏，但这只是一种直觉上的定性分析，如果我们需要精确一些，就要用到AUC，也就是ROC曲线下面积。
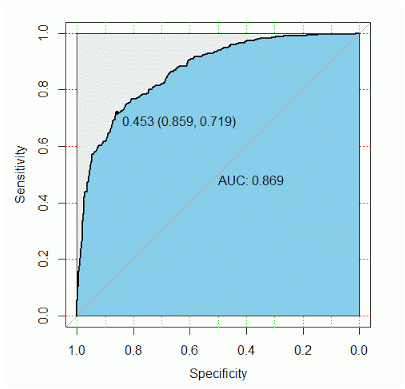
看上图，参考线的面积是0.5，ROC曲线与它偏离越大，ROC曲线就越往左上方靠拢，它下面的面积(AUC)也就越大，这里面积是0.869。我们可以根据AUC的值与0.5相比，来评估一个分类模型的预测效果。
6.1.2回归评估指标
均方差（MSE,Mean Squared Error）：
(∑(prec-act)**2)/n (prec为预测值，act为实际值，n为总样本数)
均方根差（RMSE,Root Mean Squared Error）:
就是MSE开根号
平均绝对值误差(MAE,Mean Absolute Error):
(∑|prec-act|)/n
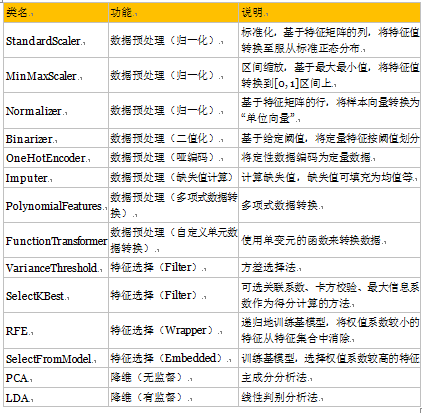
6.1.3评估指标在Sciktlearn中对应的函数
评估分类模型：
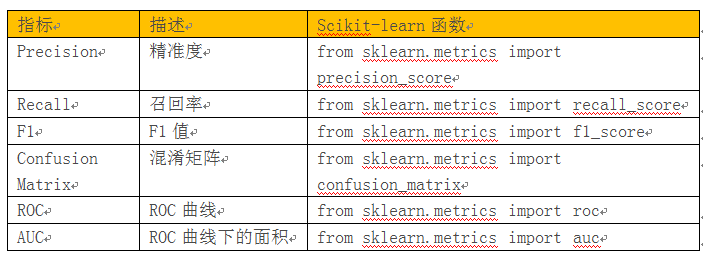
评估回归模型：
6.2模型评估与优化
对模型评估和优化时，我们常常使用训练集-验证集二划分验证（Hold-out validation）、K折交叉验证（k-Cross-validation）、超参数调优(hyperparameter tuning)等方法。三者从不同的层次对机器学习模型进行校验。Hold-out validation是评估机器学习模型泛化性能一个经典且常用的方法，通过这种方法，我们将把数据集划分为训练集和测试集，前者用于模型训练，后者用于性能的评估。
6.2.1Hold-out validation方法
使用Hold-out validation还可以采用更好的一种划分方法，把数据划分为三个部分，训练集、验证集和测试集，训练集用于模型的拟合，模型在验证集上的性能表现作为模型选择的标准，模型评估在测试集上。Hold-out validation的一般流程图如下：
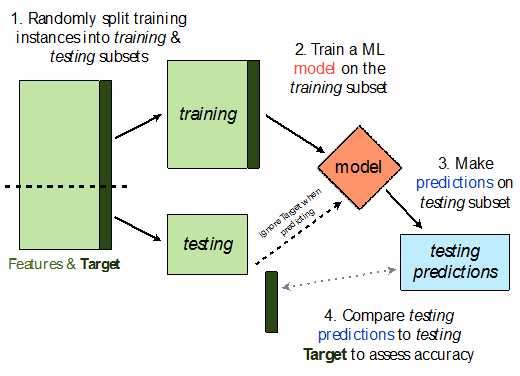
6.2.2 K-fold交叉验证
一种更好，但是计算量更大的交叉验证方法是K-fold交叉验证。如同Holdout方法，K-fold交叉验证也依赖于训练数据的若干个相互独立子集。主要的区别在于K-fold交叉验证一开始就随机把数据分割成K个不相连的子集，成为folds（一般称作K折交叉验证，K的取值有5、10或者20）。每次留一份数据作为测试集，其余数据用于训练模型。
当每一份数据都轮转一遍之后，将预测的结果整合，并与目标变量的真实值比较来计算准确率。K-fold交叉验证的图形展示如下：
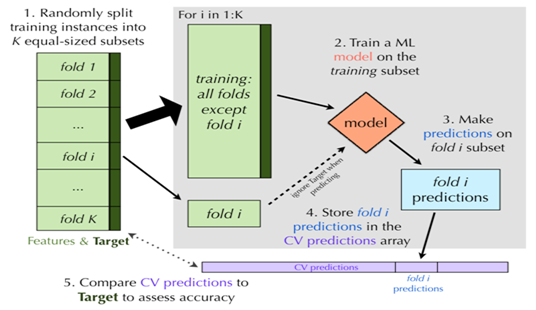
以下我们通过实例来进一步说明K-折交叉验证的使用方法及其优越性。这里我们使用UCI数据集中一个有关威斯康星乳腺癌数据集。
1）读取数据
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data', header=None)
df.head()
部分数据：
2）对标签数据转换为整数，目前是字符M(恶性)或B（良性）
X = df.loc[:, 2:].values
y = df.loc[:, 1].values
le = LabelEncoder()
y = le.fit_transform(y)
le.transform(['M', 'B'])
转换结果如下：
array([1, 0])
3）把数据划分为训练数据和测试数据，划分比例为7:3
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.20, random_state=1)
4）使用PCA对原数据集进行降维
这里我们采用管道或流水线方式，把对数据的标准化等组装在一起。
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
pipe_lr = Pipeline([('scl', StandardScaler()),
('pca', PCA(n_components=2)),
('clf', LogisticRegression(random_state=1))])
5）在训练集上进行k-折交叉验证
这里我们取k=10，采用sklearn中StratifiedKFold函数。
from sklearn.cross_validation import StratifiedKFold
kfold = StratifiedKFold(y=y_train,
n_folds=10,
random_state=1)
scores = []
for k, (train, test) in enumerate(kfold):
pipe_lr.fit(X_train[train], y_train[train])
score = pipe_lr.score(X_train[test], y_train[test])
scores.append(score)
print('Fold: %s, Class dist.: %s, Acc: %.3f' % (k+1, np.bincount(y_train[train]), score))
print('\nCV accuracy: %.3f +/- %.3f' % (np.mean(scores), np.std(scores)))
运行结果如下：
Fold: 1, Class dist.: [256 153], Acc: 0.891
Fold: 2, Class dist.: [256 153], Acc: 0.978
Fold: 3, Class dist.: [256 153], Acc: 0.978
Fold: 4, Class dist.: [256 153], Acc: 0.913
Fold: 5, Class dist.: [256 153], Acc: 0.935
Fold: 6, Class dist.: [257 153], Acc: 0.978
Fold: 7, Class dist.: [257 153], Acc: 0.933
Fold: 8, Class dist.: [257 153], Acc: 0.956
Fold: 9, Class dist.: [257 153], Acc: 0.978
Fold: 10, Class dist.: [257 153], Acc: 0.956
CV accuracy: 0.950 +/- 0.029
准确率达到95%,说明结果还不错。
6）改进的k-折交叉验证
k-折交叉验证比较耗资源，而且抽取数据是随机的，这就可能导致有些分发中的类别比例不很恰当，是否有更好方法？以下我们采用分层k-折交叉验证法，使用scikit-learn中cross_val_score。
scores = cross_val_score(estimator=pipe_lr,
X=X_train,
y=y_train,
cv=10,
n_jobs=1)
print('CV accuracy scores: %s' % scores)
print('CV accuracy: %.3f +/- %.3f' % (np.mean(scores), np.std(scores)))
运算结果如下：
CV accuracy scores: [ 0.89130435 0.97826087 0.97826087 0.91304348 0.93478261 0.97777778 0.93333333 0.95555556 0.97777778 0.95555556]
CV accuracy: 0.950 +/- 0.029
n_jobs参数很特别，使用这个参数，我们可以把K轮的交叉验证分布到几个CPU块上，如果n_jobs=2就是2块，如果n_jobs=-1，则系统将利用所有CPU进行计算。
6.3 利用验证曲线查看是否过拟合或欠拟合
验证曲线反应参数与性能指标之间的关系图，通过验证曲线图有利于定位过拟合或欠拟合等问题，是提高模型性能的有效工具。以下我们以建立在上个数据集的逻辑斯谛模型中的正则化参数C与准确率间的关系为例，使用validation_curve函数，该函数对分类算法，默认使用分层K折交叉验证来评估模型性能，使用scikit-learn来绘制验证曲线。
myfont = fm.FontProperties(fname='/home/hadoop/anaconda3/lib/python3.6/site-packages/matplotlib/mpl-data/fonts/ttf/simhei.ttf')
from sklearn.learning_curve import validation_curve
param_range = [0.001, 0.01, 0.1, 1.0, 10.0, 100.0]
train_scores, test_scores = validation_curve(
estimator=pipe_lr,
X=X_train,
y=y_train,
param_name='clf__C',
param_range=param_range,
cv=10)
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(param_range, train_mean,
color='blue', marker='o',
markersize=5, label='训练准确率')
plt.fill_between(param_range, train_mean + train_std,
train_mean - train_std, alpha=0.15,
color='blue')
plt.plot(param_range, test_mean,
color='green', linestyle='--',
marker='s', markersize=5,
label='验证准确率')
plt.fill_between(param_range,
test_mean + test_std,
test_mean - test_std,
alpha=0.15, color='green')
plt.grid()
plt.xscale('log')
plt.legend(loc='lower right',prop=myfont)
plt.xlabel('参数C',fontproperties=myfont,size=12)
plt.ylabel('准确率',fontproperties=myfont,size=12)
plt.ylim([0.8, 1.0])
plt.tight_layout()
plt.show()
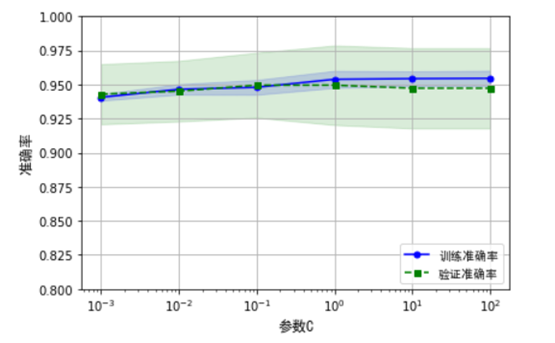
从以上图形不难看出，参数C的最优点是0.1附近，如果加大正则化强度（C较小），会导致一定程度的欠拟合；如果降低正则化强度，可能导致模型的过拟合。
6.4 利用参数网格搜索调优模型
在机器学习中，有两类参数：一种是通过训练数据得到的参数，如回归模型、神经网络中系统；一种是需要单独进行优化的参数，如正则化系统、迭代次数、树的深度等，这类参数称为调优参数，又称为超参。
这里我们将介绍一种功能强大的超参数优化方法，即网格搜索(grid search)方法，通过这种方法自动选择最优参数组合，并选择最优模型。以下利用Scikit learn中GridSearchCV函数来实现网格搜索。
from sklearn.svm import SVC
pipe_svc = Pipeline([('scl', StandardScaler()),
('clf', SVC(random_state=1))])
param_range = [0.0001, 0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0]
param_grid = [{'clf__C': param_range,'clf__gamma': param_range, 'clf__kernel': ['linear','rbf']}]
gs = GridSearchCV(estimator=pipe_svc,
param_grid=param_grid,
scoring='accuracy',
cv=10,
n_jobs=-1)
gs = gs.fit(X_train, y_train)
print(gs.best_score_)
print(gs.best_params_)
运行结果：
0.978021978021978
{'clf__C': 0.1, 'clf__gamma': 0.0001, 'clf__kernel': 'linear'}
由此可知，最优参数组合是：clf__C=0.1 , clf__kernel='linear', clf__gamma=0.0001
这个组合对应模型性能达到近98%。
此外，还有随机搜索（randomized search）、嵌套交叉验证选择模型等方法。大家可作为练习去练习。这里就不展开来说了。
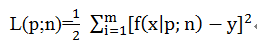
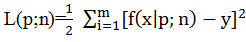最小的参数p；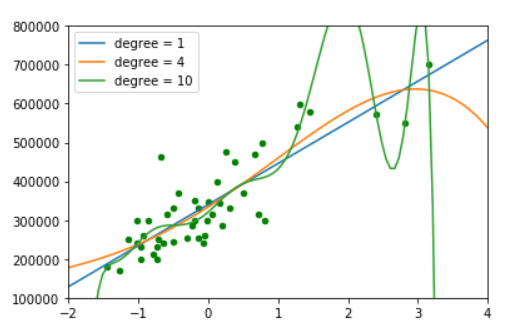
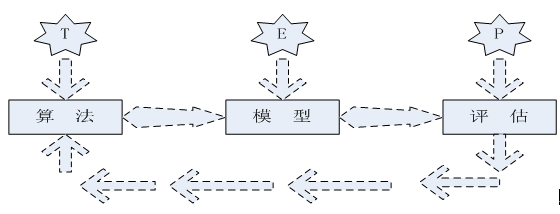
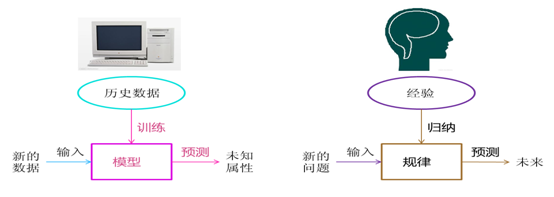
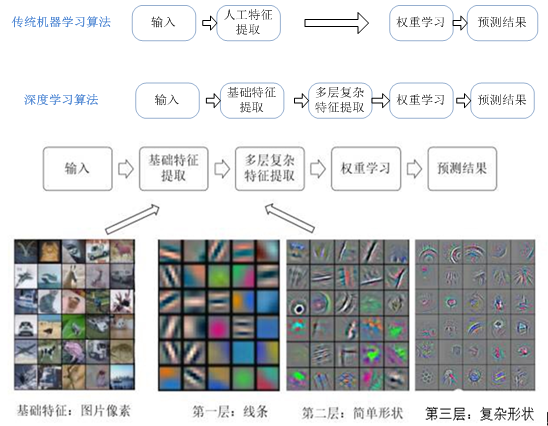
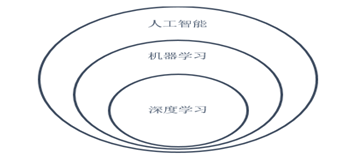
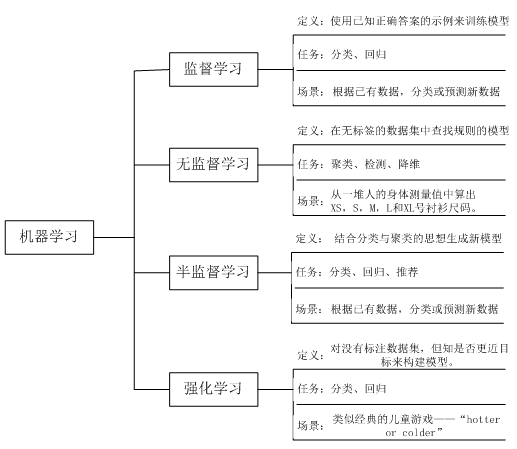
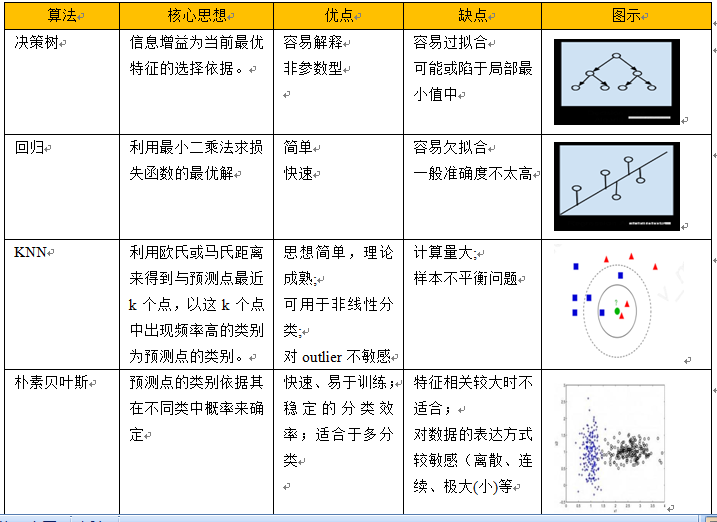
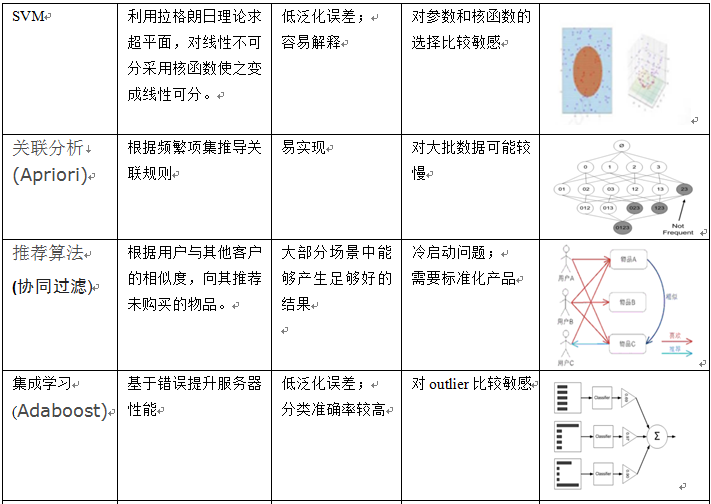
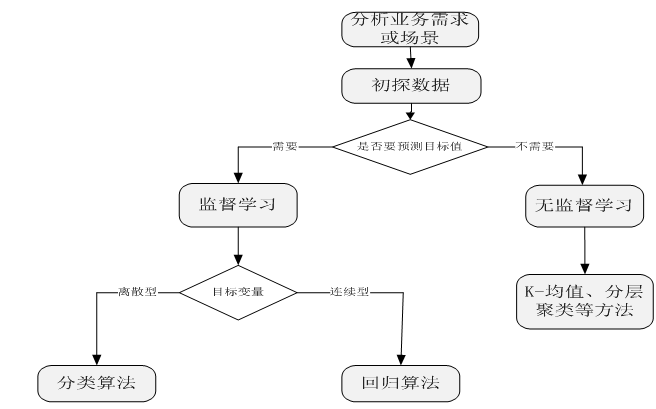
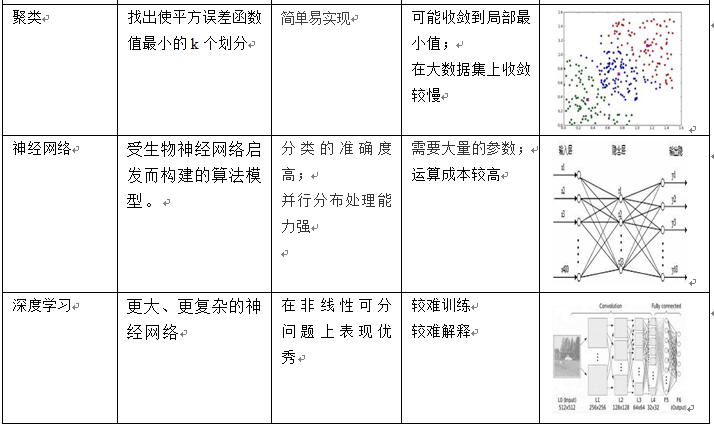当我们接到一个数据分析或挖掘的任务或需求时，如果希望用机器学习来处理，首要任务是根据任务或需求选择合适算法，选择哪种算法较合适？分析的一般步骤为：
