Python技术交流与分享

第12章 化繁为简的高手----正则化方法

12.1 正则化简介

在机器学习中，很多被显式地设计用来减少测试误差的策略，统称为正则化。正则化旨在减少泛化误差而不是训练误差。目前有许多正则化策略。有些策略向机器学习模型添加限制参数值的额外约束，如L1、L2等；有些策略向目标函数增加额外项对参数值进行软约束，如作为约束的范数惩罚等。这些惩罚和约束通常用来使模型更简单，以便提高模型的泛化能力，当然也有些正则化，如集成方法，是为了结合多个假说来更好解释训练数据。
正则化是机器学习领域的中心问题之一，其重要性只有优化问题才能与之匹敌。
正则化的作用、原理，我们还是先从几张图来说明吧，图形直观明了，易说明问题。

（图1 测试误差与训练误差）

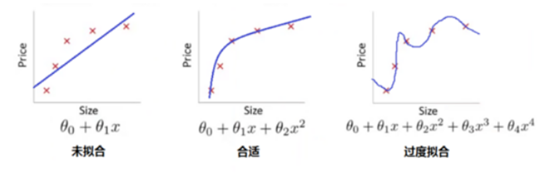
（图2 根据房屋面积预测房价几个回归模型）

这两个图说明了：
（1）、图1说明了，模型不是越复杂越好，训练精度随复杂度逐渐变小；测试误差刚开始随着模型复杂度而变小，但当复杂度超过某点之后，测试误差不但不会变小，反而会越来越大；
（2）、图2是对图1的一个示例说明。

上面我们讲了正则化的主要目的就是提高模型的泛化能力，或降低模型的测试误差。在实际模型中，它是如何实现的呢？
我们以图2中最右边这个图来说，其模型是一个4次多项式，因它把一些噪音数据也包括进来了，所以导致模型很复杂，实际上房价与房屋面积应该是2次多项式函数，如图2中间这个图。

当然这里我们取10000只是用来代表一个"大值"，现在，如果我们要最小化这个函数，那么为了最小化这个新的代价函数，我们要让 θ3 和 θ4 尽可能小。因为，如果你在原有代价函数的基础上加上 10000 乘以 θ3 这一项 ，那么这个新的代价函数将变得很大，所以，当我们最小化这个新的代价函数时， 我们将使 θ3 的值接近于 0，同样 θ4 的值也接近于 0，就像我们忽略了这两个值一样。如果我们做到这一点（ θ3 和 θ4 接近 0 ），那么我们将得到一个近似的二次函数。如下图：

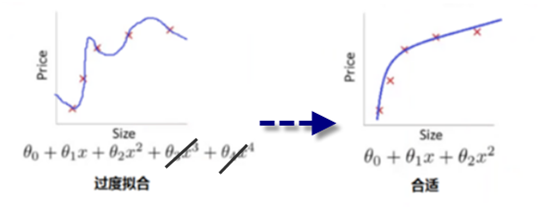
图3 利用正则化提升模型泛化能力

12.2 机器学习中常用的两种正则化策略

机器学习中几乎都可以看到损失函数后面会添加一个额外项，常用的额外项一般有两种，一般英文称作ℓ1-norm和ℓ2-norm，中文称作L1正则化和L2正则化，或者L1范数和L2范数。
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型，使用L1正则化的模型建叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。下式是Python中Lasso回归的损失函数，式中加号后面一项α||w||1即为L1正则化项。

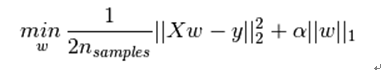
下式是Python中Ridge回归的损失函数，式中加号后面一项α||w||22即为L2正则化项。

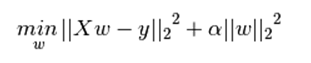
一般回归分析中回归w表示特征的系数，从上式可以看到正则化项是对系数做了处理（限制）。L1正则化和L2正则化的说明如下：
L1正则化是指权值向量w中各个元素的绝对值之和，通常表示为〖||w||〗_1
L2正则化是指权值向量w中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为〖||w||〗_2
一般都会在正则化项之前添加一个系数，Python中用α表示，一些文章也用λ表示。这个系数需要用户指定。

12.3.正则化的主要作用

L1正则化和L2正则化的作用：
L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择
L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合
1）L1正则化和特征选择
假设有如下带L1正则化的损失函数：

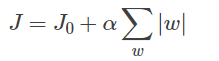
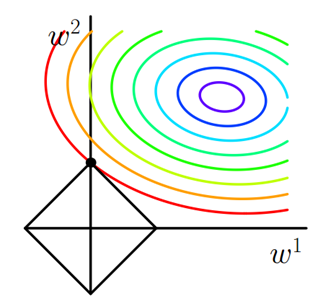
图4 L1正则化

同样可以画出他们在二维平面上的图形，如下：

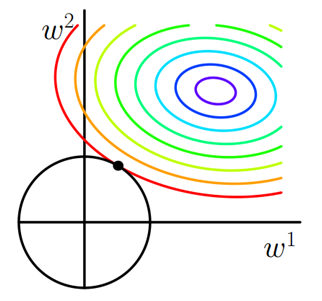
图5 L2正则化

2）L2正则化和过拟合
拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，提高模型的鲁棒性。
那为什么L2正则化可以获得值很小的参数？
以线性回归中的梯度下降法为例。假设要求的参数为θ，h_θ (x)是我们的假设函数，那么线性回归的代价函数如下：

其中λ就是正则化参数。从上式可以看到，与未添加L2正则化的迭代公式相比，每一次迭代，θj都要先乘以一个小于1的因子（如1-αλ/m），从而使得θj不断减小，因此总得来看，θ是不断减小的。
L1正则化一定程度上也可以防止过拟合。L1可以是权重系数逼近于0或等于0，这样可以简化模型，提高模型的泛化能力，从而达到与L2正则化类似的效果。

12.4 逻辑回归中使用正则化实例分析

这里我们以逻辑回归实例来具体说明，在算法中如何利用正则化策略惩罚参数值的。

因此，减少正则化参数倒数C的值就相当于增强正则化的强度，以下我们通过绘制对四个权重系数进行L2正则化的图像予以展示。

1）导入数据

2）把数据集划分为训练集和测试集，划分比例为7:3

3）对逻辑回归加入正则化项，并对C的不同取值，对权重的影响图形化。

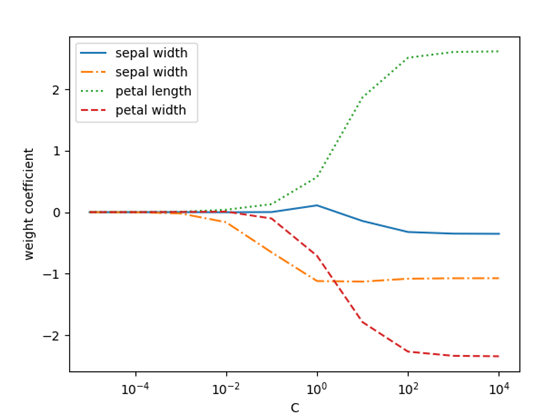
图6 利用正则化控制逻辑回归权重参数值

从上图我们不难看出，如果我们减小参数C的值，即增强正则化项的强度，可以使权重系统逐渐收缩。

12.5 Dropout正则化简介

Dropout是Srivastava等人在2014年的一篇论文中提出的一种针对神经网络模型的正则化方法 Dropout: A Simple Way to Prevent Neural Networks from Overfitting。
Dropout的做法是在训练过程中按一定比例（比例参数可设置）随机地忽略一些神经元。这些神经元被随机地“抛弃”了。也就是说它们在正向传播过程中对于下游神经元的贡献效果暂时消失了，反向传播时该神经元也不会有任何权重的更新。
随着神经网络模型不断地学习，神经元的权值会与整个网络的上下文相匹配。神经元的权重针对某些特征进行调优，具有一些特殊化。周围的神经元则会依赖于这种特殊化，如果过于特殊化，模型会因为对训练数据过拟合而变得脆弱不堪。神经元在训练过程中的这种依赖于上下文的现象被称为复杂的协同适应（complex co-adaptations）。
这么做的效果就是，网络模型对神经元特定的权重不那么敏感。这反过来又提升了模型的泛化能力，不容易对训练数据过拟合。
Dropout训练的集成包括所有从基本的基础网络除去非输出单元形成 子网络,如在图7所示。

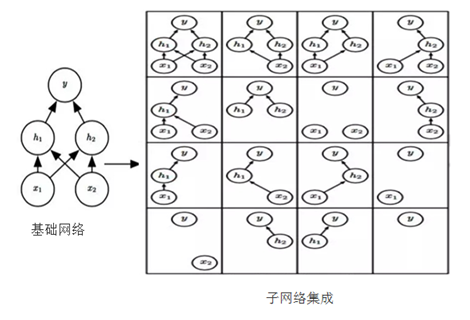
图 7 基础网络Dropout为多个子网络

Dropout训练由所有子网络组成的集成,其中子网络通过从基本网络中删除非输出单元构 建。我们从具有两个可见单元和两个隐藏单元的基本网络开始。这四个单元有十六个可能的子集。 右图展示了从原始网络中丢弃不同的单元子集而形成的所有十六个子网络。在这个小例子中,所 得到的大部分网络没有输入单元或没有从输入连接到输出的路径。当层较宽时,丢弃所有从输入 到输出的可能路径的概率变小,所以这个问题对于层较宽的网络不是很重要。

较先进的神经网络基于一系列仿射变换和非线性变换,我 们可以将一些单元的输出乘零就能有效地删除一个单元。这个过程需要对模型一些 修改,如径向基函数网络,单元的状态和参考值之间存在一定区别。为了简单起见, 我们在这里提出乘零的简单Dropout算法,但是它被简单地修改后,可以与从网络中 移除单元的其他操作一起工作。
回想一下使用Bagging学习,我们定义 k 个不同的模型,从训练集有替换采样 构造 k 个不同的数据集,然后在训练集 i 上训练模型 i。Dropout的目标是在指数 级数量的神经网络上近似这个过程。具体来说,训练中使用Dropout,我们使用基 于minibatch的学习算法和小的步长,如梯度下降等。我们每次在minibatch加载一个 样本,然后随机抽样应用于网络中所有输入和隐藏单元的不同二值掩码。对于每个 单元,掩码是独立采样的。掩码值为 1 的采样概率(导致包含一个单元)是训练开 始前固定一个超参数。它不是模型当前参数值或输入样本的函数。通常一个输入单 元包括的概率为 0.8,一个隐藏单元包括的概率为 0.5。然后,我们运行之前一样的 前向传播、反向传播以及学习更新。图8说明了在Dropout下的前向传播。

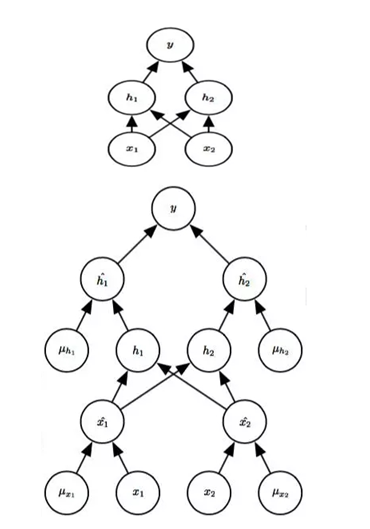
图 8
在使用Dropout的前馈网络中前向传播的示例。(顶部) 在此示例中,我们使用具有两个输入 单元,具有两个隐藏单元的隐藏层以及一个输出单元的前馈网络。(底部) 为了执行具有Dropout的 前向传播,我们随机地对向量 μ 进行采样,其中网络中的每个输入或隐藏单元对应一项。μ 中的 每项都是二值的且独立于其他项采样。每项为 1 的概率是超参数,对于隐藏层通常为 0.5,对于输 入通常为 0.8。网络中的每个单元乘以相应的掩码,然后正常地继续通过网络的其余部分前向传 播。这相当于从图7中随机选择一个子网络并通过它前向传播。

12.6 使用Dropout的小技巧

1）通常丢弃率控制在20%~50%比较好，可以从20%开始尝试。如果比例太低则起不到效果，比例太高则会导致模型的欠学习。
2）在大的网络模型上应用。当dropout用在较大的网络模型时更有可能得到效果的提升，模型有更多的机会学习到多种独立的表征。
3）在输入层（可见层）和隐藏层都使用dropout。在每层都应用dropout被证明会取得好的效果。
4）增加学习率和冲量。把学习率扩大10~100倍，冲量值调高到0.9~0.99.
5）限制网络模型的权重。大的学习率往往导致大的权重值。对网络的权重值做最大范数正则化等方法被证明会提升效果。

12.7 小结

L1、L2是我们常见正则化方式，正则化在机器学习中运用非常广泛，而且功能很强大，经常用来提升模型的泛化能力，此外，正则化策略还包括dropout、数据集增强等，甚至提前终止、集成方法、参数绑定与共享等都与正则化有千丝万缕的关系。其中有些正则化策略这里不展开来说了，后续在深度学习中我们会介绍。

本章参考以下博客或书：
http://www.cnblogs.com/jianxinzhou/p/4083921.html
http://blog.csdn.net/jinping_shi/article/details/52433975
《Python机器学习》塞巴斯蒂安.拉施卡 著